Dynamic Buckling of Functionally Graded Timoshenko Beam under Axial Load
-
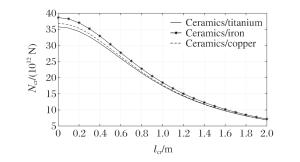
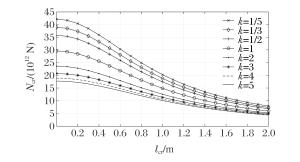
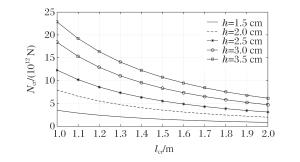
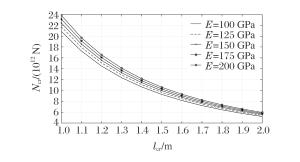
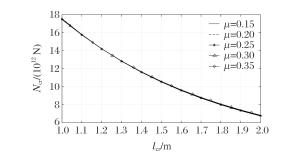
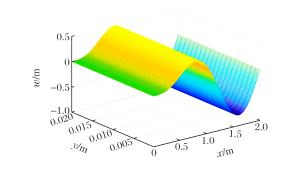
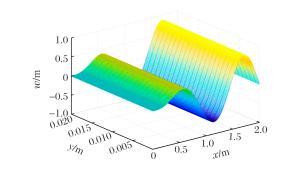
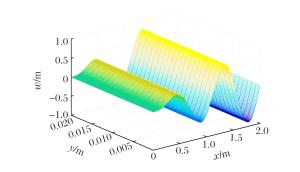
摘要: 假设功能梯度材料Timoshenko梁各项物性参数只沿厚度方向按幂函数进行连续变化，研究了功能梯度材料Timoshenko梁的动力屈曲。基于一阶剪切理论，采用Hamilton原理推导出轴向载荷作用下，功能梯度材料Timoshenko梁动力屈曲的控制方程。利用里兹法与棣莫弗公式相结合，获得了功能梯度材料Timoshenko梁在夹支-固支边界条件下动力屈曲临界载荷的解析表达式和屈曲解。应用MATLAB编程计算，讨论了功能梯度材料Timoshenko梁的几何尺寸、梯度指数、模态数、材料构成、泊松比以及弹性模量对临界载荷的影响。结果表明：功能梯度材料Timoshenko梁动力屈曲临界载荷随梁长度的增大而减小，随着梯度指数的增大而减小，随模态数的增大而增大，说明冲击载荷越大，高阶模态越容易被激发；随着泊松比和弹性模量的增大而增大，且泊松比的影响较小，而弹性模量的影响较大。由于剪切项的影响，临界载荷-临界长度的关系曲线在加载端变化趋势平缓。随着模态数的增大，梁的屈曲模态越为复杂。Abstract: In this study, we investigated the dynamic buckling of the functionally graded Timoshenko beam whose property parameters continuously change according to the power function along the thickness direction.Based on the first order shear deformation theory, we derived the governing equation of the dynamic buckling of functionally graded material Timoshenko beams under axial step loading by using the Hamilton's principle.Using the Ritz method combining with the de Moivre's formula, we obtained the buckling solution and the expression of the critical load of the dynamic buckling of functionally graded material Timoshenko beam under the clamped-fixed boundary condition.Then, the influence of geometric size, gradient index, modal number, material composition, Poisson's ratio and elastic modulus on the critical load by MATLAB calculation was discussed.The results show that the critical load of the functionally graded material Timoshenko beam decreases with the increase of beam length and the gradient index, and increases with the increase of the modal number, showing that the higher modal number is more easily excited by the increase of impact load.Furthermore, the critical load increases with the increase of the Poisson's ratio and the elastic modulus, and the effect of elastic modulus is greater than Poisson's ratio.The critical load-critical length curve tends to be gentle at the loading end because of the influence of shear term.Buckling mode of beam becomes more complicated when the modal number increases.
-
Key words:
- functionally graded material /
- dynamic buckling /
- critical load /
- Ritz method /
- de Moivre's formula
-
图 2 不同材料构成下临界载荷与临界长度的关系
Figure 2. Relationship between critical load and critical length for different materials
图 3 不同梯度指数下临界载荷与临界长度的关系
Figure 3. Relationship between critical load and critical length for different gradient indexes
图 4 不同模态数下临界载荷与临界长度的关系
Figure 4. Relationship between critical load and critical length for different modal numbers
图 5 不同截面高度下临界载荷与临界长度的关系
Figure 5. Relationship between critical load and critical length for different heights
图 6 不同弹性模量下临界载荷与临界长度的关系
Figure 6. Relationship between critical load and critical length for different elasticity modulus
图 7 不同泊松比下临界载荷与临界长度的关系
Figure 7. Relationship between critical load and critical length for different Poisson's ratios
表 1 材料各项参数
Table 1. Material parameters
Material Elasticity modulus
E/GPaDensity
ρ/ (g·cm-3)Poisson's ratio
μCeramic 385 3.96 0.23 Titanium 108.5 4.54 0.41 Iron 155 7.86 0.291 Copper 119 8.96 0.326 
下载: 导出CSV
-
[1] BIRMAN V, BYRD L W.Modeling and analysis of functionally graded materials and structures[J]. Applied Mechanics Reviews, 2007, 60(5):195-216. doi: 10.1115/1.2777164 [2] GUPTA A, TALHA M.Recent development in modeling and analysis of functionally graded materials and structures[J]. Progress in Aerospace Sciences, 2015, 79:1-14. doi: 10.1016/j.paerosci.2015.07.001 [3] NAEBE M, SHIRVANIMOGHADDAM K.Functionally graded materials:a review of fabrication and properties[J]. Applied Materials Today, 2016, 5:223-245. doi: 10.1016/j.apmt.2016.10.001 [4] KOCATURK T, AKBAŞ Ş D.Post-buckling analysis of Timoshenko beams made of functionally graded material under thermal loading[J]. Structural Engineering & Mechanics, 2012, 41(6):775-789. doi: 10.1007/s10999-010-9132-4 [5] KOCATURK T, AKBAŞ Ş D.Post-buckling analysis of Timoshenko beams with various boundary conditions under non-uniform thermal loading[J]. Structural Engineering & Mechanics, 2011, 40(3):347-371. http://www.koreascience.or.kr/article/ArticleFullRecord.jsp?cn=KJKHB9_2011_v40n3_347 [6] PAUL A.Non-linear thermal post-buckling analysis of FGM Timoshenko beam under non-uniform temperature rise across thickness[J]. Engineering Science & Technology:An International Journal, 2016, 19(3):1608-1625. https://www.sciencedirect.com/science/article/pii/S2215098616302853 [7] ŞIMŞEK M.Buckling of Timoshenko beams composed of two-dimensional functionally graded material (2D-FGM) having different boundary conditions[J]. Composite Structures, 2016, 149:304-314. doi: 10.1016/j.compstruct.2016.04.034 [8] ELTAHER M A, KHAIRY A, SADOUN A M, et al.Static and buckling analysis of functionally graded Timoshenko nanobeams[J]. Applied Mathematics &Computation, 2014, 229(229):283-295. https://www.sciencedirect.com/science/article/pii/S0096300313013556 [9] RAHIMI G H, GAZOR M S, HEMMATNEZHAD M, et al.On the postbuckling and free vibrations of FG Timoshenko beams[J]. Composite Structures, 2013, 95(1):247-253. https://www.sciencedirect.com/science/article/pii/S0263822312003625 [10] LI S R.Relations between buckling loads of functionally graded Timoshenko and homogeneous Euler-Bernoulli beams[J]. Composite Structures, 2013, 95(1):5-9. [11] KAHYA V, TURAN M.Finite element model for vibration and buckling of functionally graded beams based on the first-order shear deformation theory[J]. Composites Part B:Engineering, 2017, 109:108-115. doi: 10.1016/j.compositesb.2016.10.039 [12] KIANI Y.Thermal buckling analysis of functionally graded material beams[J]. International Journal of Mechanics & Materials in Design, 2010, 6(3):229-238. doi: 10.1007/s10999-010-9132-4 [13] ANANDRAO K S.Thermal post-buckling analysis of uniform slender functionally graded material beams[J]. Structural Engineering & Mechanics, 2010, 36(5):545-560. https://www.researchgate.net/publication/264077187_Thermal_post-buckling_analysis_of_uniform_slender_functionally_graded_material_beams [14] AKBAŞ Ş D, KOCATÜRK T.Post-buckling analysis of functionally graded three-dimensional beams under the influence of temperature[J]. Journal of Thermal Stresses, 2013, 36(12):1233-1254. doi: 10.1080/01495739.2013.788397 [15] RYCHLEWSKA J.A new approach for buckling analysis of axially functionally graded beams[J]. Journal of Applied Mathematics & Computational Mechanics, 2015, 14(2):95-102. [16] FEREZQI H Z, TAHANI M, TOUSSI H E.Analytical approach to free vibrations of cracked Timoshenko beams made of functionally graded materials[J]. Mechanics of Advanced Materials & Structures, 2010, 17(5):353-365. doi: 10.1080/15376494.2010.488608?scroll=top&needAccess=true [17] 徐华, 李世荣.一阶剪切理论下功能梯度梁与均匀梁静态解之间的相似关系[J].工程力学, 2012, 29(4):161-167. http://www.cnki.com.cn/Article/CJFDTotal-GTLX201403013.htmXU H, LI S R.Analogous relationship between the static solutions of functionally graded beams and homogeneous beams based on the first-order shear deformation theory[J]. Engineering Mechanics, 2012, 29(4):161-167. http://www.cnki.com.cn/Article/CJFDTotal-GTLX201403013.htm [18] KIRCHHOFF G.Ueber das Gleichgewicht und die Bewegung eines unendlich dünnen elastischen Stabes[J]. Journal FüR Die Reine Und Angewandte Mathematik, 2009, 1859(56):285-313. https://eudml.org/doc/147766 [19] 李楠, 韩志军, 路国运.基于里兹法研究复合材料层合板的动力屈曲问题[J].振动与冲击, 2016, 35(10):180-184. http://industry.wanfangdata.com.cn/jt/Detail/Periodical?id=Periodical_zdycj201610029LI N, HAN Z J, LU G Y.Research on dynamic buckling of laminated composite plates using Ritz method[J]. Journal of Vibration and Shock, 2016, 35(10):180-184. http://industry.wanfangdata.com.cn/jt/Detail/Periodical?id=Periodical_zdycj201610029 -
下载:
点击查看大图
图(11) / 表(1)
计量
- 文章访问数: 6896
- HTML全文浏览量: 2882
- PDF下载量: 184
