Numerical Analysis of Falling Response of Large Warhead in Cabin
-
摘要: 采用ANSYS/LS-DYNA动力学仿真软件模拟战斗部跌落试验,基于材料本构模型对战斗部跌落安全性进行预测,得到了不同状态下战斗部跌落的结构变形和装药响应数据。结果表明:带舱战斗部45°倾斜跌落时,壳体和主装药受到的应力和过载均最小,但舱体变形最严重;战斗部大端向下垂直跌落时,壳体受到的应力较小,但炸药受到的应力和过载均最大,工况最恶劣。研究结论为带舱大型战斗部的跌落考核试验提供了指导。Abstract: In this study, we used the ANSYS/LS-DYNA software to simulate the fall test of the cabin warhead in order to predict its safety performance, and obtained the structural stress deformation and charge overload response of the combat simulation of the warhead in different states.The results show that the stress and overload of the shell and the main charge are the smallest when the cabin warhead is tilted at 45°, but the deformation of the shell is the most severe; and the stress of the shell is small when the large part of the warhead is dropped vertically, but the stress and overload of the charge are the largest, indicating the worst assessment posture.The actual fall test of the large warhead in cabin is successfully passed, and the numerical simulation can provide theoretical support.
-
Key words:
- ammunition safety /
- fall test /
- cabin warhead
-
表 1 炸药材料本构方程
Table 1. Constitutive equation of explosive materials
ρ/(kg·m-3) E/GPa υ σY/MPa ETAN/MPa FAIL tDEL C 1700 8.56 0.25 209 231 0 0 0 表 2 靶板材料模型及参数
Table 2. Target material model and the parameters
ρ/(kg·m-3) E/GPa υ N 7850 200 0.3 0 表 3 扩爆药柱材料模型及参数
Table 3. Booster explosive material model and the parameters
ρ/(kg·m-3) E/GPa υ σY/MPa ETAN/MPa C P vP 1630 2.90 0.25 190 210 0 0 0 表 4 破片材料模型及参数
Table 4. Fragment material model and the parameters
ρ/(kg·m-3) E/GPa υ σY/MPa ETAN/MPa β 19 250 350 0.25 1.5 170 1 表 5 跌落试验仿真计算结果
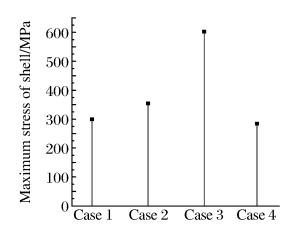
Table 5. Fall test simulation results
Case Maximum stress of shell/MPa Maximum stress of charge/MPa Maximum charge overload/g 1 299.2 23.30 312.1 2 354.0 15.84 237.4 3 602.6 7.86 161.7 4 283.9 2.98 33.1 -
[1] 江明, 唐成, 袁宝慧.导弹战斗部安全性试验评估[J].四川兵工学报, 2015, 36(7):6-9.JIANG M, TANG C, YUAN B H.Summary of missile warhead's safety tests evaluation[J]. Journal of Sichuan Ordnance, 2015, 36(7):6-9. [2] 董三强, 冯顺山, 金俊.弹药安全性能评价模型研究[J].兵工学报, 2011, 32(4):421-425. http://s.wanfangdata.com.cn/Export/Export.aspx?scheme=NoteExpressDONG S Q, FENG S S, JIN J.Researches on safety assessment model of ammunitions[J]. Acta Armamentarii, 2011, 32(4):421-425. http://s.wanfangdata.com.cn/Export/Export.aspx?scheme=NoteExpress [3] 董海山.钝感弹药的由来及重要意义[J].含能材料, 2006, 14(5):323-329. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HNCL201112001066.htmDONG H S.The importance of the insensitive munitions[J]. Chinese Journal of Energetic Materials, 2006, 14(5):323-329. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HNCL201112001066.htm [4] 国防科工委司令部. 弹药安全性试验规程: GJB 3857-99[S]. 1999. [5] 高大元, 申春迎, 黄谦, 等.炸药件在模拟跌落试验中的响应[J].火炸药学报, 2012, 35(5):13-16.GAO D Y, SHEN C Y, HUANG Q.Reaction of explosive subassembly under simulated drop test[J]. Chinese Journal of Explosive & Propellants, 2012, 35(5):13-16. [6] WATT D, DESCHAMBAULT E, TOUZE P.Insensitive munitions (IM):a key aspect of improved munitions safety[J]. Chinese Journal of Energetic Materials, 2006, 14(5):323-329. [7] 王晓峰, 赵省向. 战术战斗部用炸药[M]. 西安: 中国兵器工业第二〇四研究所, 2003.WANG X F, ZHAO S X.Tactical warhead with explosives[M]. Xi'an:China Ordnance Industry Institute, 2003. [8] 孙锦山.高能炸药的非理想爆轰性能研究[J].含能材料, 2004, 12(增刊2):341-344. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hncl2004z1086SUN J S.Research on non-ideal detonation performance of high energy explosives[J]. Chinese Journal of Energetic Materials, 2004, 12(Suppl 2):341-344. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hncl2004z1086 [9] CHIDESTER S K, GREEN L G, LEE C G. A frictional work predictive method for the initiation of solid high explosives from low pressure impacts[C]//10th International Detonation Symposium. Boston, MA: Office of Naval Research, 1993: 785-792. http://www.osti.gov/scitech/servlets/purl/10103000 [10] 宋浦, 肖川, 沈飞.炸药非理想爆轰能量释放与能量利用的关系[J].火炸药学报, 2011, 34(2):44-46.SONG P, XIAO C, SHEN F.Relationship of energy release and utilization of non-ideal detonation of explosive[J]. Chinese Journal of Explosive & Propellants, 2011, 34(2):44-46. [11] 王晨, 陈朗, 鲁峰.炸药跌落响应数值模拟分析[J].含能材料, 2012, 12(6):748-753.WANG C, CHEN L, LU F.Numerical simulation for spigot tests[J]. Chinese Journal of Energetic Materials, 2012, 12(6):748-753. [12] 王晨, 陈朗, 何乐.低强度冲击下炸药点火的数值模拟[J].火炸药学报, 2012, 35(2):44-48. http://www.cqvip.com/xueke/543WANG C, CHEN L, HE L.Numerical simulation of explosive ignition under low impact loading[J]. Chinese Journal of Explosive & Propellants, 2012, 35(2):44-48. http://www.cqvip.com/xueke/543 [13] TARVER C M, HALLQUIST J O, ERICKSON L M. Modeling of shortpulse duration shock initiation of solid explosive[C]//Proceedings of 8th Symposium (International) on Detonation. Albuquerque, 1985: 951-961. https://www.osti.gov/scitech/biblio/5571329 [14] 时党勇, 李裕春, 张胜民.基于ANSYS/LS-DYNA 8.1进行显示动力分析[M].北京:清华大学出版社, 2005. [15] HALQUIST J. LS-DYNA keyword user's manual version 971[M]. Livermore, CA: Livermore Software Technology Corporation, 2007. -






 下载:
下载: