JWL Equation of State of Unreacted JOB-9003 Explosive
-
摘要: 采用火炮加载技术对JOB-9003炸药进行一维平面冲击实验,利用组合式电磁粒子速度计记录了不同位置的粒子速度变化历程,获得了炸药的冲击Hugoniot线。利用实测的冲击Hugoniot线,对三项式状态方程进行标定,确定了JOB-9003炸药的JWL状态方程参数。Abstract: One-dimensional plane impact experiments with power gun were conducted on JOB-9003 explosives.The Hugoniot relation of unreacted JOB-9003 explosive was obtained by measuring the particle velocities at different depths with magnetic gauges.Moreover, the trinomial equation of state was calibrated with the experimental Hugoniot curve, and the JWL equation of state parameters of JOB-9003 explosive were determined.
-
1. 引言
状态方程是炸药的基本性能,对研究炸药的冲击起爆、确定化学反应速率函数以及爆轰数值模拟是不可或缺的。目前,主要采用半理论半经验的方法进行状态方程研究,即先测出炸药的冲击Hugoniot线,再根据实测的Hugoniot线对理论模型中的参数进行标定。
在未反应炸药的冲击Hugoniot线研究方面,国外通常采用轻气炮加载技术,测试技术则以VISAR(Velocity Interferometer System for Any Reflector)和组合式电磁粒子速度计为主。例如:Millett等人[1]利用一级轻气炮和PVDF(Polyvinylidene Fluoride)压力计研究了高聚物粘结炸药的冲击Hugoniot线;Burns等人[2]采用电磁粒子速度计对EDC32炸药进行了一维平面冲击实验,获得了0.59~7.5 GPa压力范围内分段式线性Hugoniot关系。国内未反应炸药的冲击Hugoniot线研究则主要采用火炮加载和平面波透镜加载,测试技术从最初的锰铜压力计发展到现在的电磁粒子速度计。例如:张旭等人[3]采用锰铜压力计测量了JB9014钝感炸药和LY12铝标准样品在LY12铝飞片同时撞击下的界面压力,通过压力对比法确定了JB9014钝感炸药的冲击Hugoniot线;傅华等人[4]利用粒子速度对比法,通过电磁粒子速度计测量了PMMA(Polymethyl Methacrylate)飞片同时撞击PMMA样品和JOB-9003炸药界面的粒子速度,获得了未反应JOB-9003炸药的冲击Hugoniot关系。
目前,炸药的状态方程大多采用三项式状态方程,为此本研究利用实测的JOB-9003炸药的冲击Hugoniot线,对三项式状态方程进行标定,以确定未反应炸药JOB-9003的JWL形式的状态方程参数。
2. 实验方法
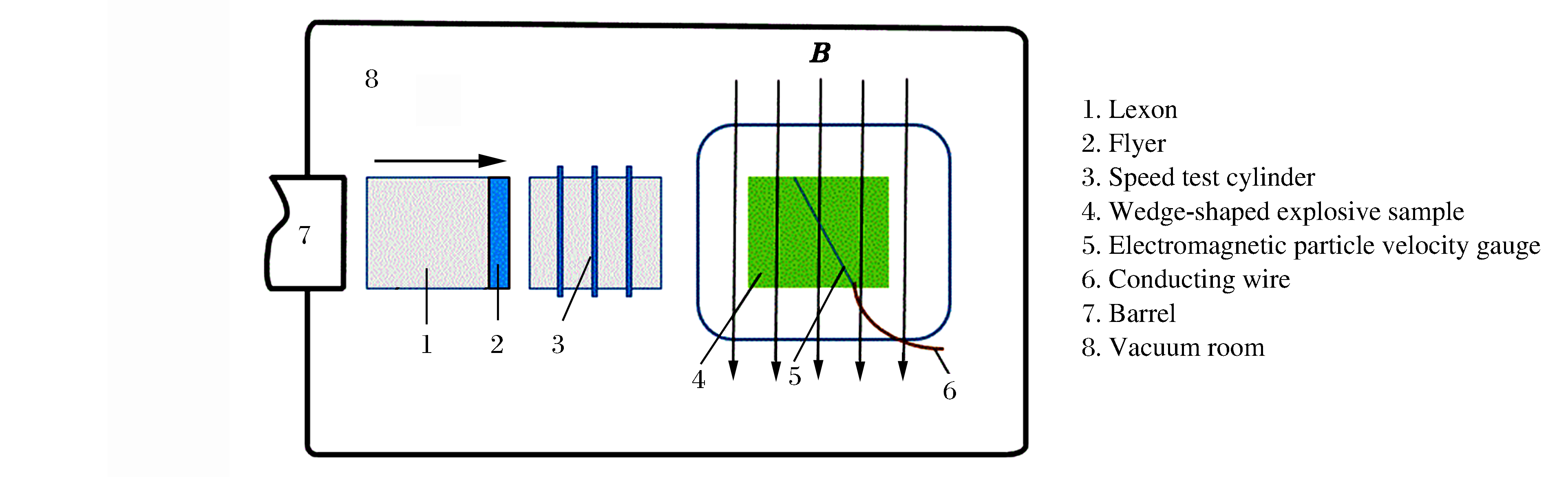
采用火炮加载技术和组合式电磁粒子速度计,对JOB-9003炸药进行一维平面冲击实验。如图 1所示,实验装置主要包括加载装置、真空靶室、Ø57 mm的Lexon弹托、Ø55 mm的蓝宝石飞片、磁通量为0.14 T的磁场装置、组合电磁粒子速度计、待测JOB-9003炸药样品。将铝基组合式电磁粒子速度计镶入具有30°倾角的炸药样品中,感应单元之间的间隔为2 mm,以保证相邻感应单元在冲击波传播方向的间距为1 mm。采用光测技术测量飞片速度,当飞片通过测速环时,先后阻断间隔为25 mm的两束信号光,通过示波器反馈的时间差计算飞片速度。组合电磁粒子速度计是基于法拉第电磁感应定律,若已知磁场强度B和切割磁力线的感应单元长度l,通过测量感生电动势ε,即可计算粒子速度up
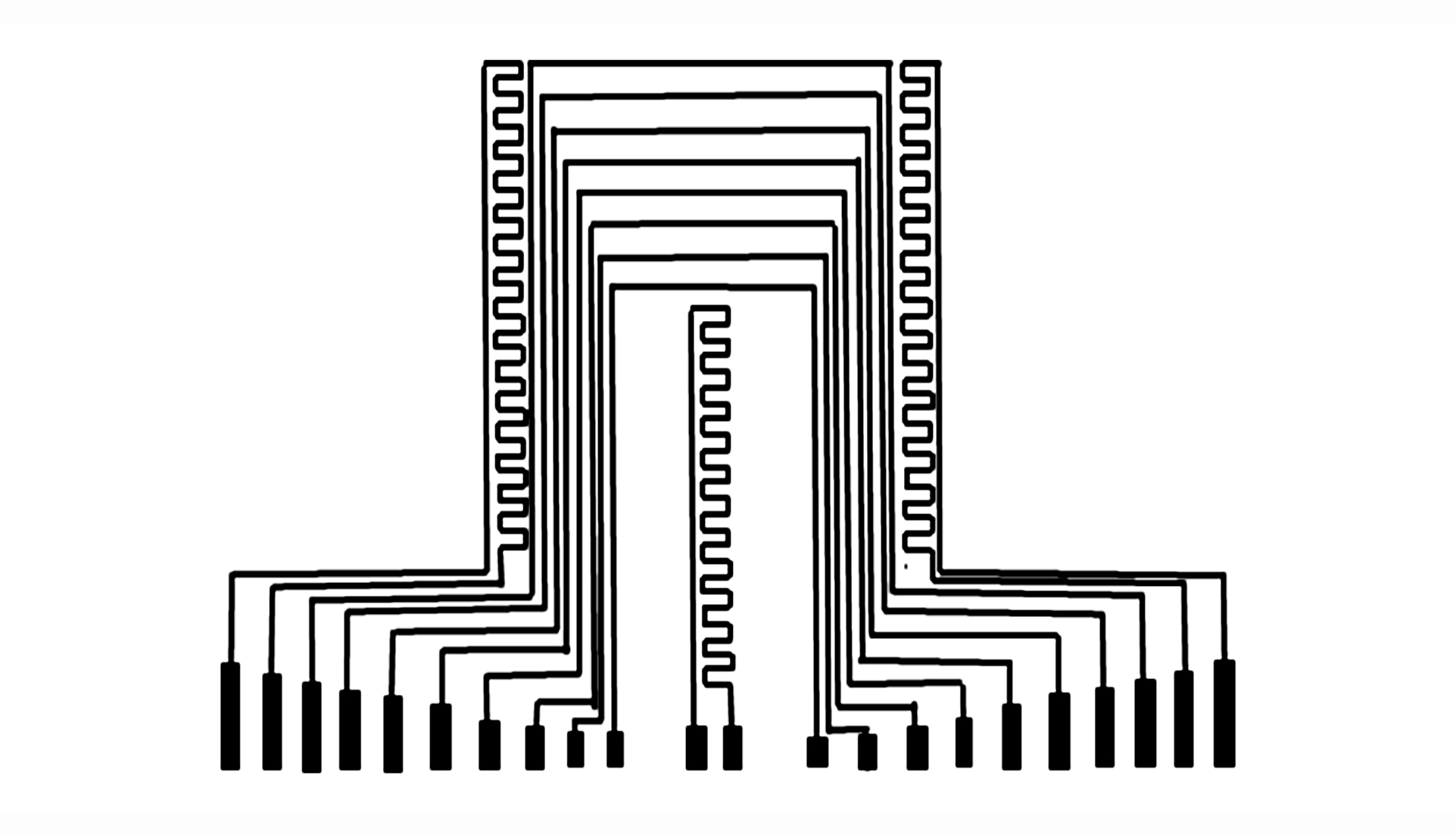
up=εBl (1) 铝基组合式电磁粒子速度计(见图 2)由1个8测点组合速度计、3个单点速度计和3个冲击波示踪器构成。单点速度计贴在炸药的前表面,用于记录冲击前端的界面粒子速度;锯齿状元件为冲击波示踪器,相邻感应单元的间距为0.5 mm,总长20 mm,共有40个测量位置,用于记录冲击波到达样品中各测量位置的时刻。
3. 实验结果与分析
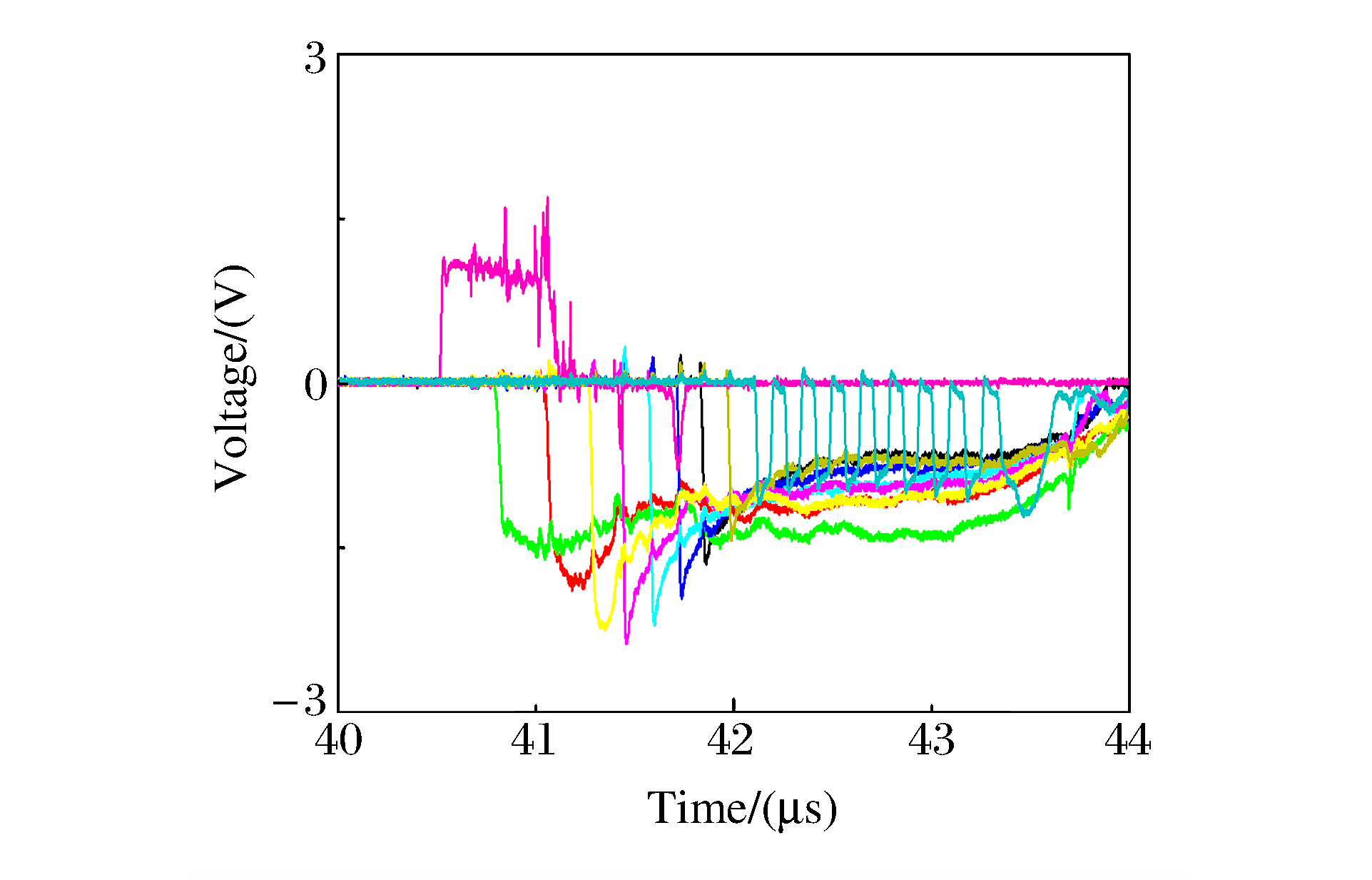
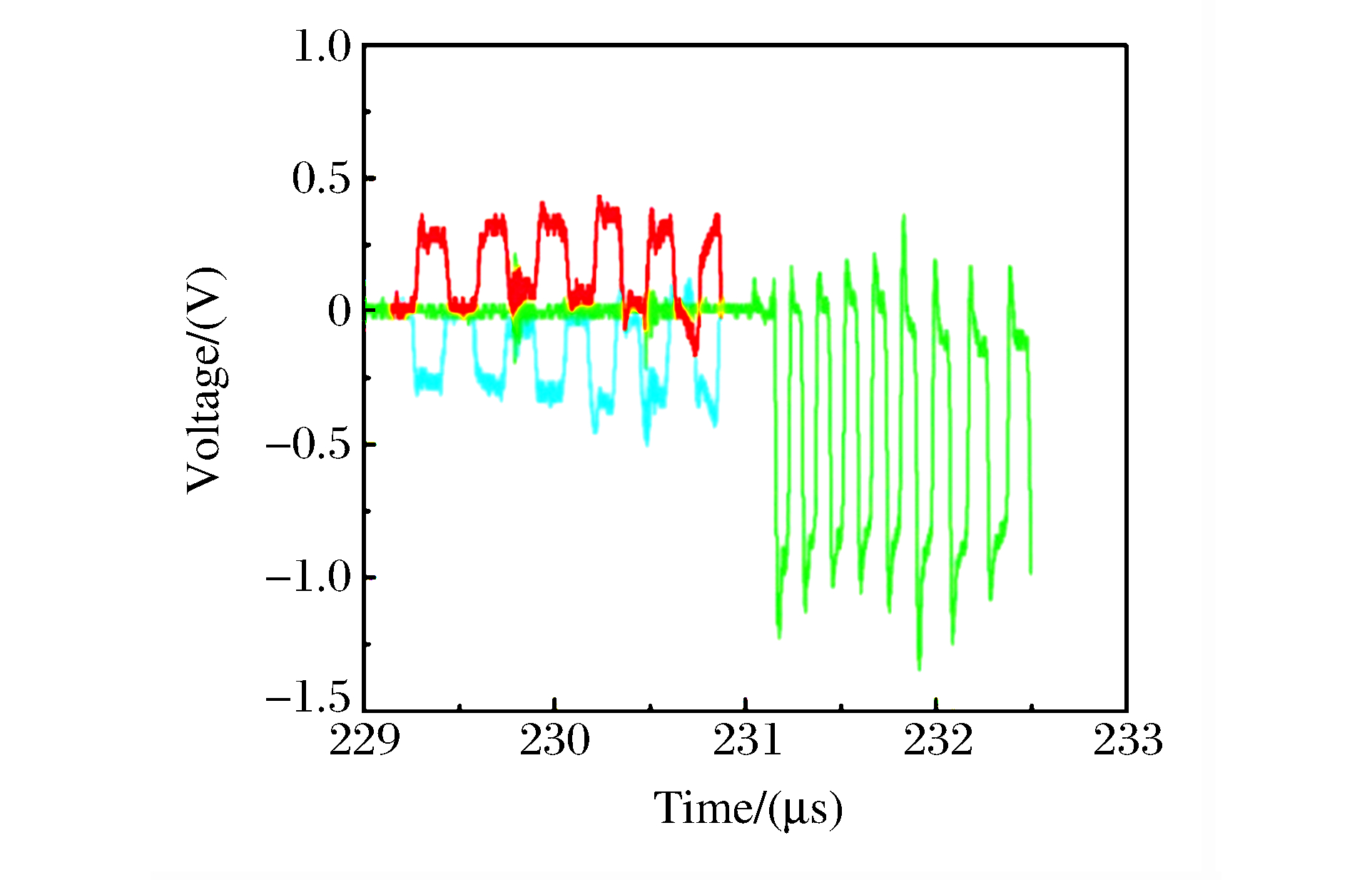
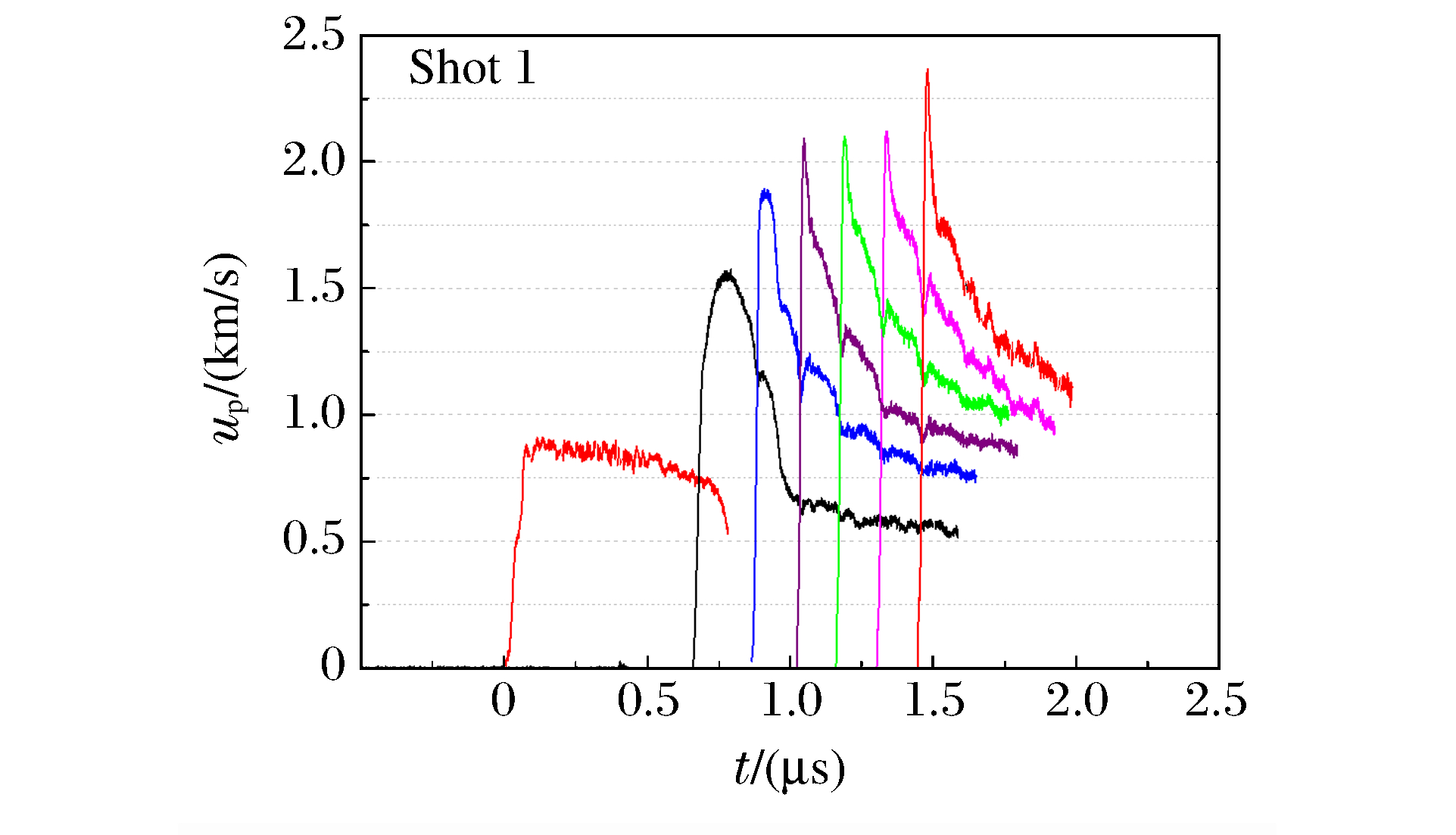
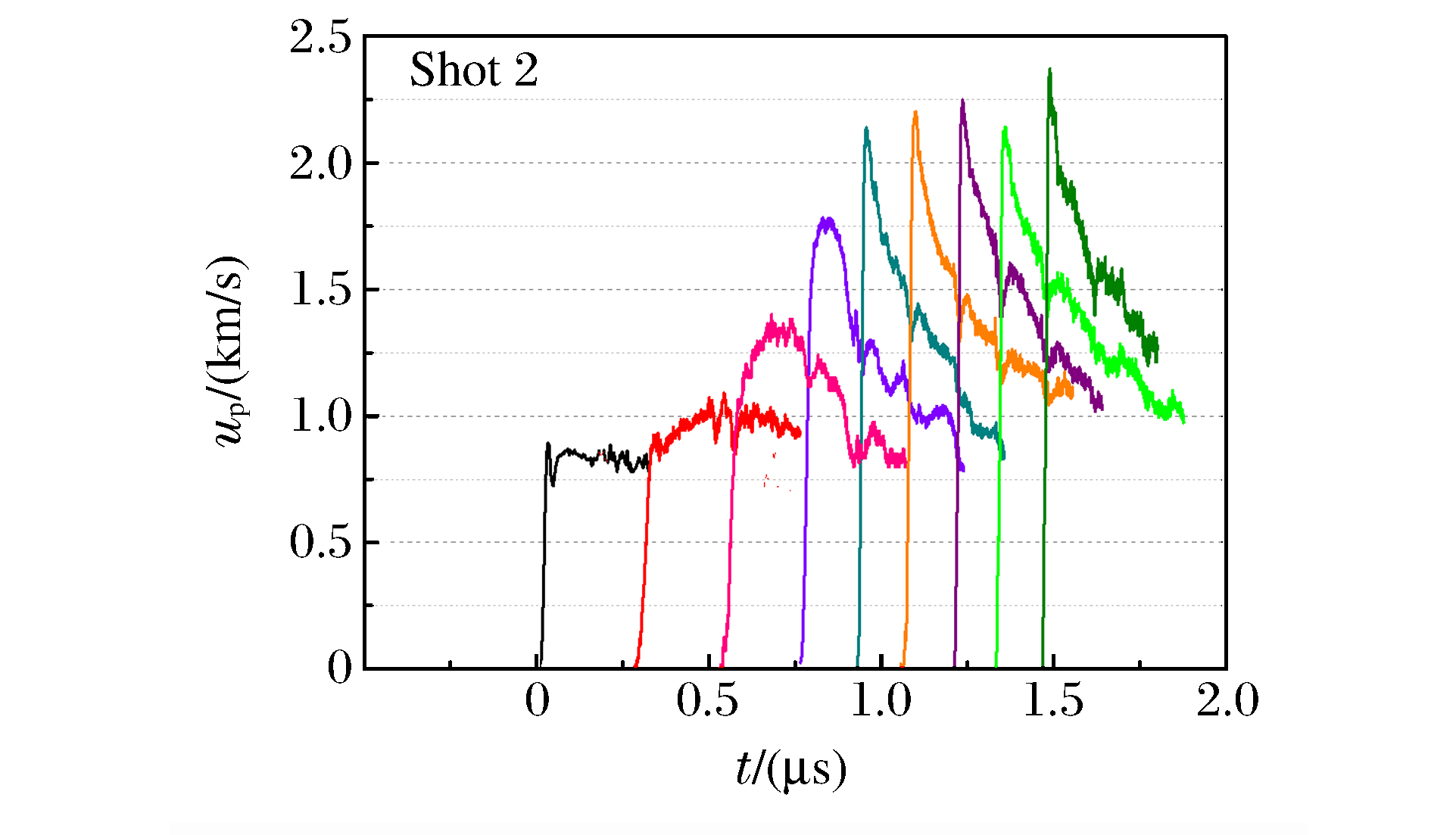
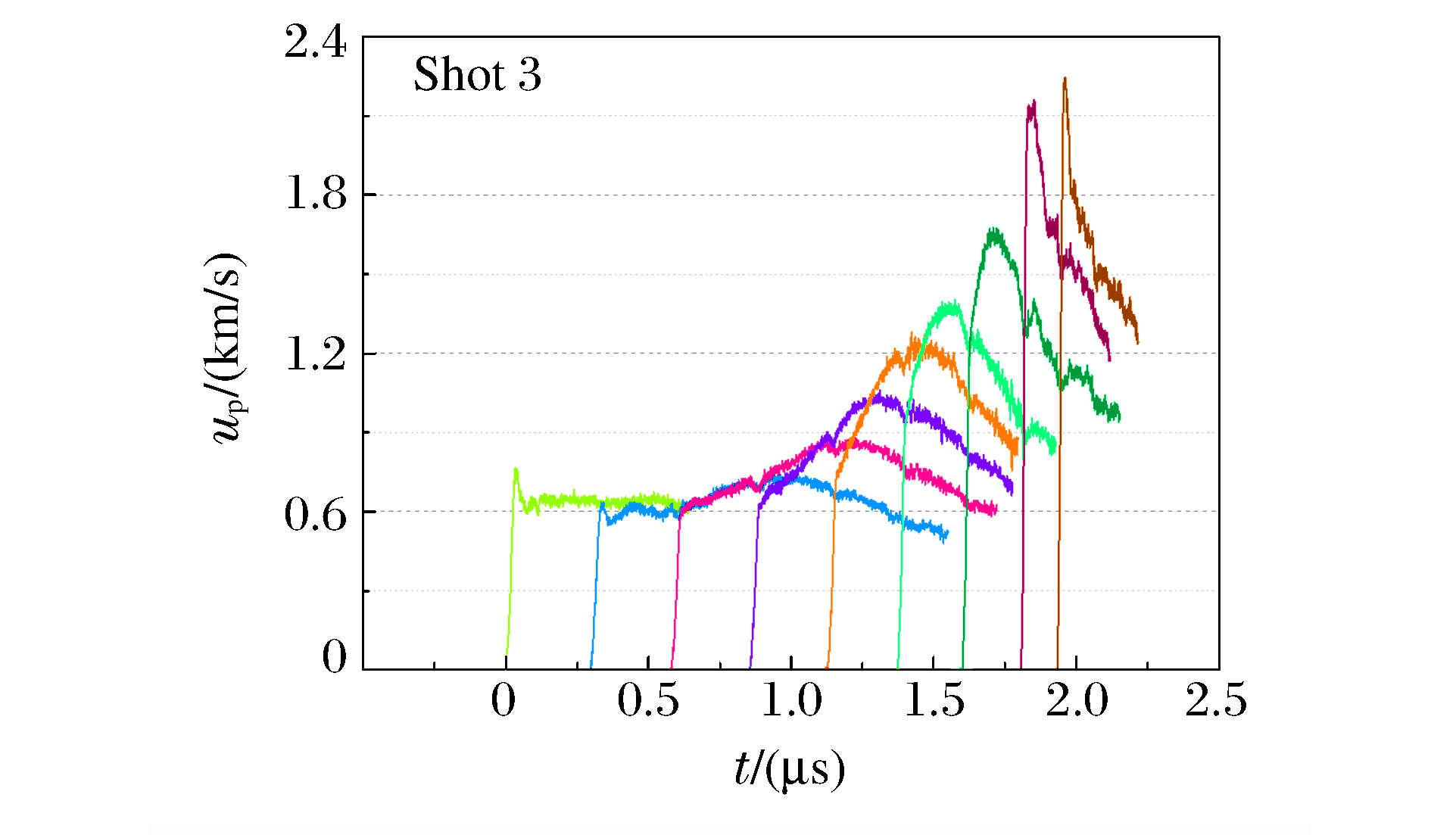
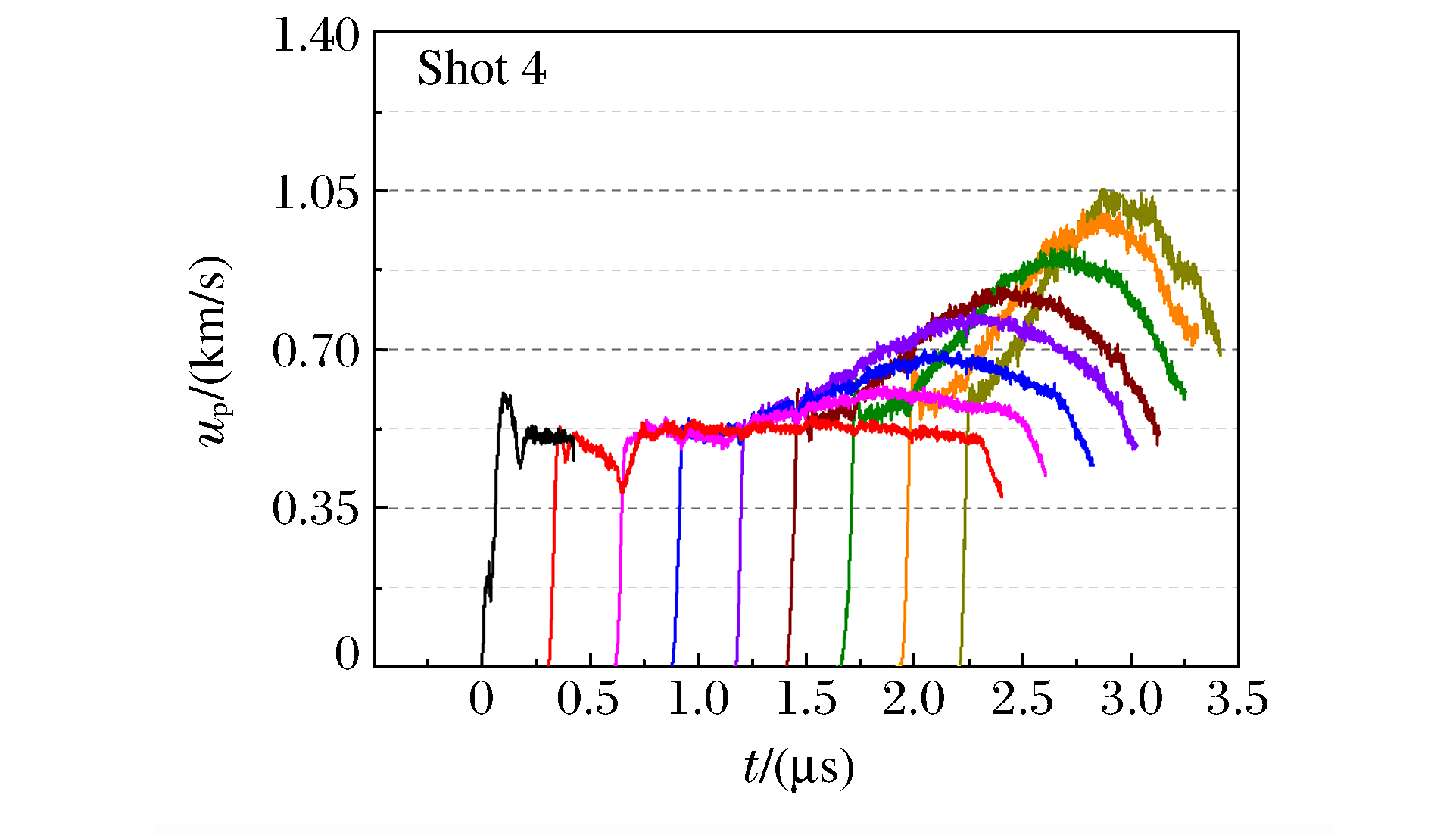
随着冲击波深入炸药,炸药中的粒子速度峰值不断增加,直至冲击转为爆轰。由前表面的单点速度计可测得界面处的粒子速度,根据冲击波到达0、1、2 mm处的时刻,可推算出界面处的冲击波速度。图 3为组合式电磁粒子速度计在示波器上显示的典型原始信号,图 4为典型的冲击波示踪器信号。通过(1)式,可获得炸药的粒子速度up随时间t变化的曲线,如图 5~图 8所示。在图 5中,由于1、2 mm处的粒子速度信号丢失,因此采用冲击波示踪器信号(见图 4)计算界面处的冲击波速度。
由于平面冲击波是一种有物质流通过的间断面,由动量守恒定律可知
pH=ρ0usup (2) 式中:pH为初始冲击压力,ρ0为炸药的初始密度,us为入射冲击波速度,up为波后界面粒子速度。在界面处,由(2)式可以得到每发实验的初始冲击压力pH,进而得到4发实验的us和up,如表 1所示。
表 1 JOB-9003炸药平面冲击实验参数Table 1. Parameters of plane impact experiments on JOB-9003 explosiveShot No. ρ0/(g/cm3) pH/(GPa) us/(km/s) up/(km/s) 1 1.844 6.28 3.892 0.875 2 1.841 6.10 3.856 0.860 3 1.845 4.17 3.480 0.650 4 1.845 3.11 3.210 0.525 利用us-up实验数据,绘制出实验压力范围内炸药的us-up关系
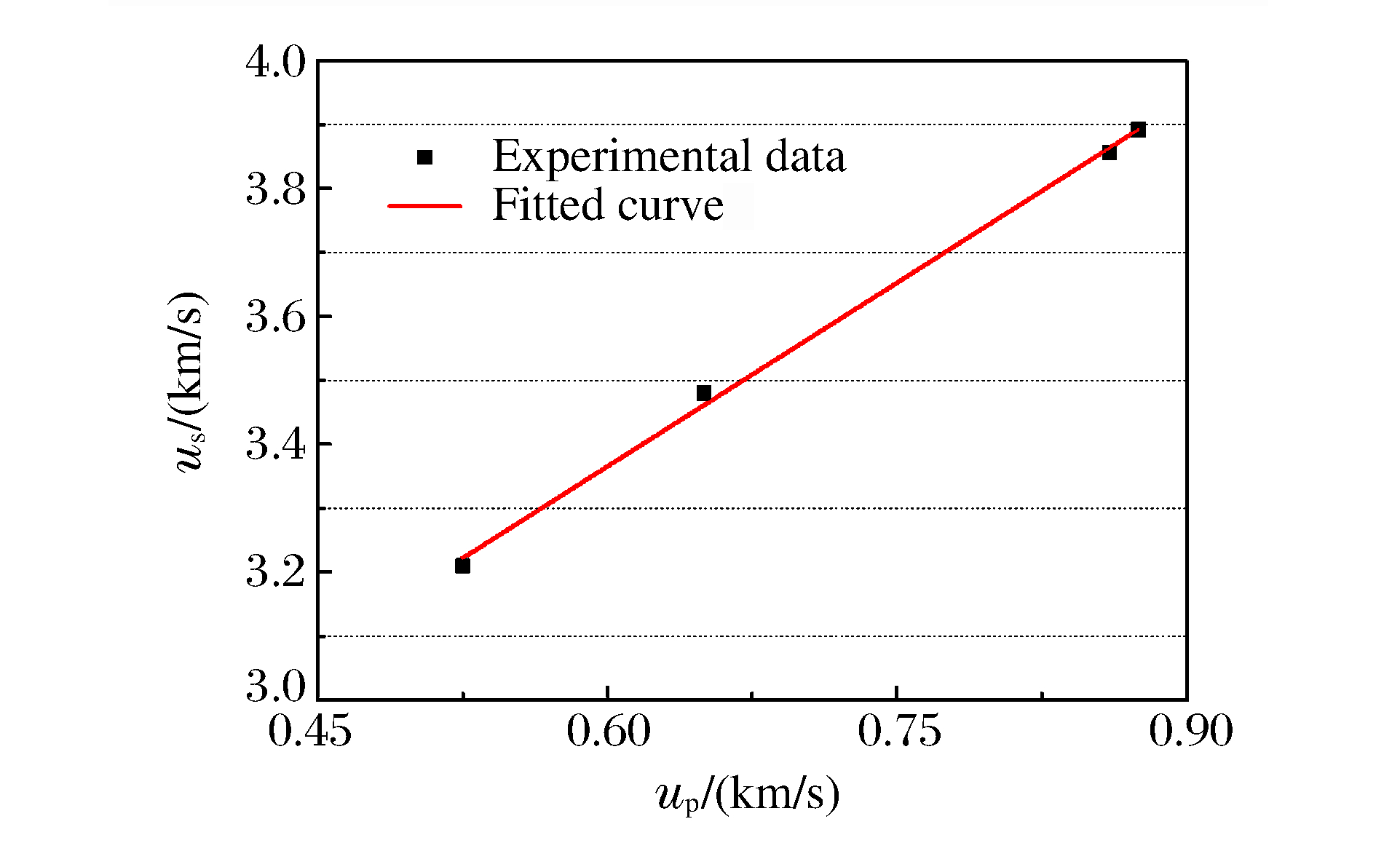
us=C0+λup (3) 式中:C0和λ为常数。对4组实验数据进行线性拟合,得到JOB-9003炸药的冲击Hugoniot关系(见图 9)
us=(2.21±0.06)+(1.91±0.08)up0.53km/s≤up≤0.87km/s (4) 4. 三项式状态方程
一般而言,无论是固体还是液体,压力p都可通过三项式状态方程表示为比容v和温度T的函数
p(v,T)=px(v)+pTN(v,T)+pTe(v,T) (5) 式中:px(v)为冷压,pTN(v, T)为晶格热振动贡献,pTe(v, T)为自由电子项贡献。对于非金属材料,可以不考虑自由电子项贡献,晶格热振动贡献可通过固体德拜模型确定,而冷压则由Grüneisen物态方程和热力学关系式求得。Grüneisen物态方程是描述晶格热振动贡献的一种特性方程
p−px=γ(v)v(E−Ex) (6) 式中:E为内能,px和Ex分别为冷能和冷压,γ(v)为Grüneisen参数。将(3)式代入平面冲击波的质量守恒、动量守恒和能量守恒关系式,则(2)式可写为
pH(v)=ρ0C20η(1−λη)2 (7) 式中:η=1-v/v0,其中v0为炸药的初始比容。通过px和Ex之间的关系以及冲击的能量守恒方程,可将(6)式变换为
Vγ(v)dExdv+Ex=−pHv2[1+2γ(v)−v0v] (8) (8) 式对相对比容v(v=v/v0)求导, 可得
vγ(v)p′x+{v0+[vγ(v)]′}px=(pHv2)′[1+2γ(v)−v0v]+pHv2[1+2γ(v)−v0v]′ (9) 式中:“′”表示对相对比容v的微分。微分方程的初值包括绝对零度下被测样品的初始比容v0K和px(v0K)。v0K=v0−∫T00avdT,其中α为体积膨胀系数,T0为室温;px(v0K)=0。Grüneisen参数γ(v)可通过热力学公式推导出[5]
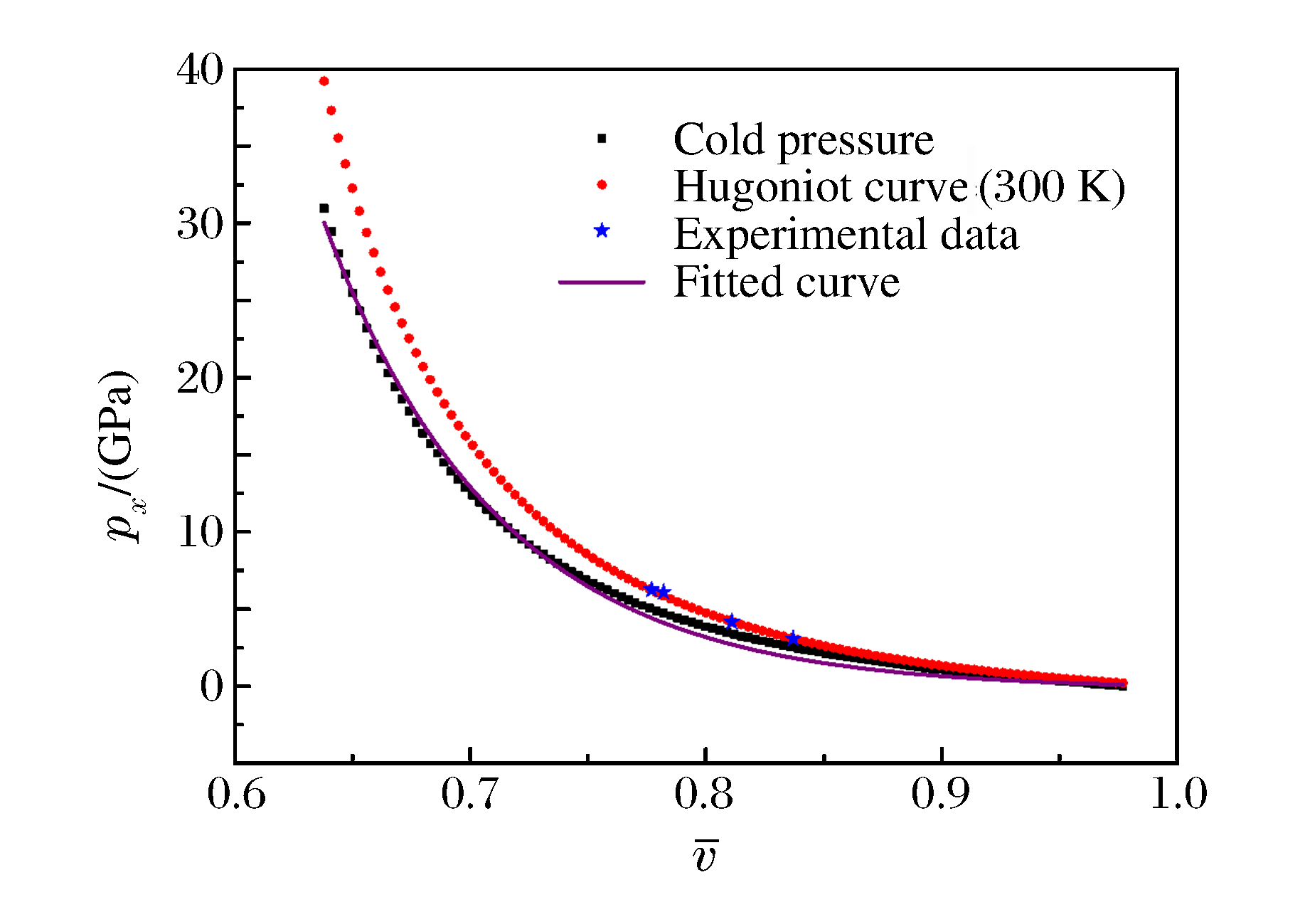
γ=us(2us−C0)[C0+(λ−1)us]−13C0us(us−C0)−λC30us(us−C0)(us+C0) (10) 由(10)式可知,在本实验压力范围内γ(v)的变化很小,取定值2.76。拟合得到的冷压曲线见图 10。
三项式状态方程中的晶格热振动贡献可由德拜模型得到[6]
pTN=ωcVγ(v)ˉvT (11) 式中:ω是与温度有关的量,cV为定容比热容。当冲击压力较低时,cV和ω可取定值。对于JOB-9003炸药,cV取1.02 J/(g·K)[7];由初始条件p(v0, T0)=0,可得到ω。联立(5)式和(11)式,得到本实验压力范围内简化的JWL形式状态方程
p=Ae−Bˉv−Ce−Dˉv+ωcVγˉvT (12) 式中:A、B、C、D为拟合参数,如表 2所示。
表 2 JOB-9003炸药的状态方程参数Table 2. Equation of state parameters of JOB-9003 explosivecV/[J/(g·K)] α/(K-1) γ A/(TPa) B C/(GPa) D ω 1.02 5.48×10-5 2.76 158.781 13.42 0.78 1.342 3.79×10-3 5. 结论
利用火炮加载技术及组合式电磁粒子速度计,进行了JOB-9003炸药的爆轰反应研究。实验原理简单,信噪比高,干扰小,对于研究低压下炸药的爆轰反应是可行的。对JOB-9003炸药进行三项式状态方程标定,在实验压力范围内与实测的Hugoniot曲线相近,效果较好。
-
表 1 JOB-9003炸药平面冲击实验参数
Table 1. Parameters of plane impact experiments on JOB-9003 explosive
Shot No. ρ0/(g/cm3) pH/(GPa) us/(km/s) up/(km/s) 1 1.844 6.28 3.892 0.875 2 1.841 6.10 3.856 0.860 3 1.845 4.17 3.480 0.650 4 1.845 3.11 3.210 0.525 表 2 JOB-9003炸药的状态方程参数
Table 2. Equation of state parameters of JOB-9003 explosive
cV/[J/(g·K)] α/(K-1) γ A/(TPa) B C/(GPa) D ω 1.02 5.48×10-5 2.76 158.781 13.42 0.78 1.342 3.79×10-3 -
[1] MILLETT J C F, BOURNE N K.The shock Hugoniot of a plastic bonded explosive and inert simulants[J].J Phys D, 2004, 37(18):2613-2617. doi: 10.1088/0022-3727/37/18/018 [2] BURNS M J, GUSTAVSEN R L, BARTRAM B D.One-dimensional plate impact experiments on the cyclotetramethylene tetranitramine (HMX) based explosive EDC32[J].J Appl Phys, 2012, 112(6):064910. doi: 10.1063/1.4752865 [3] 张旭, 池家春, 冯民贤.JB9014钝感炸药冲击绝热线测量[J].高压物理学报, 2001, 15(4):304-308. doi: 10.3969/j.issn.1000-5773.2001.04.011ZHANG X, CHI J C, FENG M X.Hugoniot relation of JB9014 insensitive high explosive[J].Chinese Journal of High Pressure Physics, 2001, 15(4):304-308. doi: 10.3969/j.issn.1000-5773.2001.04.011 [4] 傅华, 谭多望, 李金河, 等.未反应JOB-9003炸药冲击Hugoniot关系测试[J].高压物理学报, 2009, 23(6):427-432. doi: 10.3969/j.issn.1000-5773.2009.06.005FU H, TAN D W, LI J H, et al.Hugoniot relation of unreacted JOB-9003 explosive[J].Chinese Journal of High Pressure Physics, 2009, 23(6):427-432. doi: 10.3969/j.issn.1000-5773.2009.06.005 [5] 张宝坪, 张庆明, 黄风雷.爆轰物理学[M].北京:兵器工业出版社, 1997:375-402.ZHANG B P, ZHANG Q M, HUANG F L.Detonation physics[M].Beijing:Weapon Industry Press, 1997:375-402. [6] 经福谦.实验物态方程导引[M].第2版.北京:科学出版社, 1999:29-38.JING F Q.Introduction to experimental equation of state[M].2nd ed.Beijing:Science Press, 1999:29-38. [7] 董海山, 周芬芬.高能炸药及相关物性能[M].北京:科学出版社, 1989:297-299.DONG H S, ZHOU F F.High energy explosives and correlative physical properties[M].Beijing:Science Press, 1989:297-299. -








 下载:
下载:










 下载:
下载: