气相爆炸流场中TiO<sub>2</sub>纳米颗粒生长的数值分析初探

陈天梧; 罗宁; 闫鸿浩; 刘凯欣

doi:10.11858/gywlxb.2014.06.014

气相爆炸流场中TiO₂纳米颗粒生长的数值分析初探

doi: 10.11858/gywlxb.2014.06.014

陈天梧^1,,
罗宁^{1, 2, 3},
闫鸿浩⁴,
刘凯欣¹

1.
北京大学力学与空天技术系，湍流与复杂系统国家重点实验室，北京 100081
2.
中国矿业大学力学与建筑工程学院，深部岩土力学与地下工程国家重点实验室，江苏徐州 221116
3.
北京理工大学, 爆炸科学与技术国家重点实验室, 北京 100081
4.
大连理工大学工程力学系, 辽宁大连 110623

基金项目: 国家自然基金(11272081，11028206)；中央高校青年基金(2014QNA76)；中国博士后科学基金(2012M510270, 2014M551700);北京理工大学爆炸科学与技术国家重点实验室开放基金(KFJJ13-5M)

详细信息

作者简介:
陈天梧(1989—), 男，硕士，主要从事气相爆轰合成纳米功能材料研究.E-mail:chentw@pku.edu.cn

中图分类号: O389
计量
- 文章访问数: 6530
- HTML全文浏览量: 2114
- PDF下载量: 273
出版历程
- 收稿日期: 2013-02-02
- 修回日期: 2013-04-25

Numerical Analysis of the Formation of TiO₂ Nanoparticles in Gas Phase Explosion Flow Field

1.
LTCS and Department of Mechanics & Aerospace Engineering, College of Engineering, Peking University, Beijing 100871, China
2.
State Key Laboratory for Geo-mechanics and Deep Underground Engineering, School of Mechanics and Civil Engineering, China University ofMining and Technology, Xuzhou 221116, China
3.
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
4.
Department of engineering mechanics, DaLian University of Technology, Dalian 110623, China

摘要

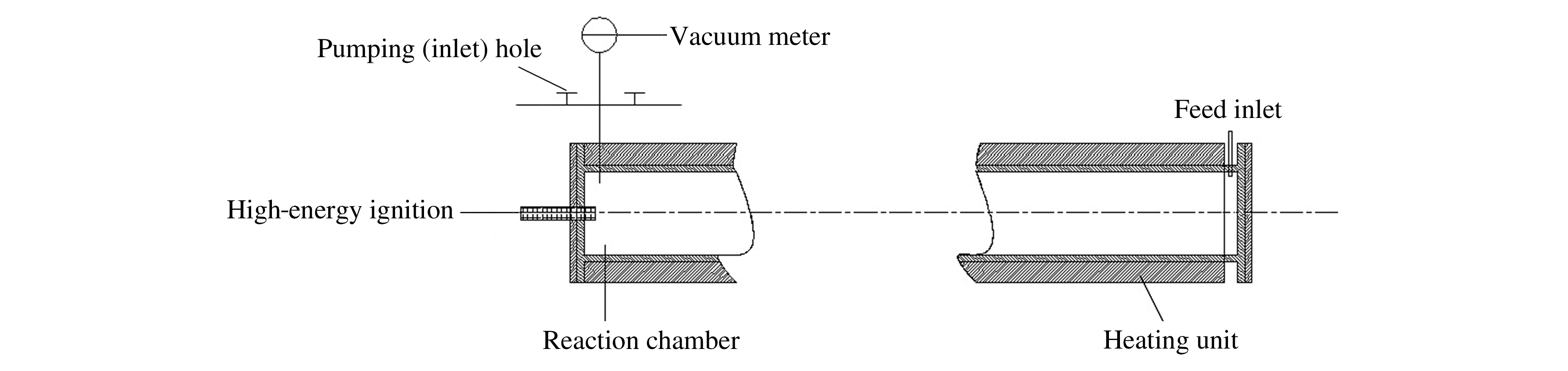
摘要: 气相爆炸制备TiO₂纳米颗粒的实验成果在近年来多有报道，但对颗粒成长的模拟尚不多见。引入一种气溶胶的单分散性物理模型(Kruis模型)，将其应用于气相爆炸流场中TiO₂纳米颗粒生长的数值模拟，结合气相爆炸制备实验进行对比分析。结果表明，通过控制前驱体反应组分，气相爆轰合成了直径范围为20~150 nm的球形TiO₂纳米颗粒。数值模拟得到的颗粒大小与实验观测结果基本一致。影响纳米颗粒生长的主要因素包括反应温度、颗粒浓度及反应时间。
- 气相爆炸 /
- 二氧化钛(TiO₂) /
- 纳米颗粒成长 /
- 数值分析
Abstract: A monodisperse model was introduced to simulate the TiO₂ nanoparticles synthesization during the gas phase explosion.The calculation of this model was based on the experimental results and CJ theory which describes the gas phase explosion field.After a numerical analysis and theoretical explanation, the model was validated in comparison with the experimental results of gas phase explosion synthesis of TiO₂.TiO₂ nanoparticles with diameter of 20-150 nm were obtained.The results show that the numerical analysis can give a rapid predictive result of TiO₂ nanoparticles synthesis, and the main factors affecting the growth of nanoparticles are reaction temperature, concentration of particles and reaction time.
- gas phase explosion /
- titanium dioxide (TiO₂) /
- nanoparticles formation /
- numerical analysis

HTML全文

图 1 气相爆炸装置示意图

Figure 1. Schematic of the gas explosion device

下载: 全尺寸图片幻灯片

图 2 制备产物的TEM图

Figure 2. TEM images of the gas phase explosion products

下载: 全尺寸图片幻灯片

图 3 气相爆炸产物的XRD图谱

Figure 3. XRD pattern of the gas phase explosion products

下载: 全尺寸图片幻灯片

图 4 不同温度下原生颗粒直径d_p、聚合颗粒数密度N和生成颗粒数量n_p随时间的增长

(a) Diameter distribution (b) Density of obtained nanoparticles (c) Number of TiO₂ nanoparticles

Figure 4. The diameter distribution of native nanoparticle, the density of obtained nanoparticles and the growth of TiO₂ nanoparticles with time

下载: 全尺寸图片幻灯片

表 1 气相爆炸实验条件及TiO₂纳米颗粒特征

Table 1. Experimental conditions and TiO₂ characteristics by gas-phase detonation

Sample No.	TiCl₄:H₂:O₂ (Volume ratio)	Mass fraction of components/(%)		Particle diameter/(nm)
Sample No.	TiCl₄:H₂:O₂ (Volume ratio)	Anatase	Rutile	Anatase	Rutile
1	1.0:3.0:1.0	11.2	88.8	22.12	41.94
2	1.0:2.5:1.0	28.1	71.9	19.64	37.61
3	1.0:2.0:1.0	45.0	55.0	26.24	37.70
Note:The particle diameters are calculated by Scherrer equation.

下载: 导出CSV

参考文献(17)

[1]	Gelbard F, Seinfeld J H. Numerical solution of the dynamic equation for particulate systems[J]. J Comput Phys, 1978, 28(3): 357-375. doi: 10.1016/0021-9991(78)90058-X
[2]	Wu J J, Nguyen H V, Flagan R C, et al. Evaluation and control of particle properties in aerosol reactors[J]. Aiche J, 1988, 34(8): 1249-1256. doi: 10.1002/aic.690340803
[3]	Kruis F E, Kusters K A, Pratsinis S E, et al. A simple model for the evolution of the characteristics of aggregate particles undergoing coagulation and sintering[J]. Aerosol Sci Techno, 1993, 19(4): 514-526. doi: 10.1080/02786829308959656
[4]	Appel J, Bockhorn H, Wulkow M. A detailed numerical study of the evolution of soot particle size distributions in laminar premixed flames[J]. Chemosphere, 2001, 42(5/6/7): 635-645.
[5]	Kumar J, Warnecke G. A note on moment preservation of finite volume schemes for solving growth and aggregation population balance equations[J]. SIAM J Sci Comput, 2010, 32(2): 703-713. doi: 10.1137/090757356
[6]	Al Zaitone B, Schmid H J, Peukert W. Simulation of structure and mobility of aggregates formed by simultaneous coagulation, sintering and surface growth[J]. J Aerosol Sci, 2009, 40(11): 950-964. doi: 10.1016/j.jaerosci.2009.08.007
[7]	欧阳欣, 闫鸿浩, 刘津开, 等.纳米TiO₂粉体的气相爆轰制备[J].高压物理学报, 2007, 21(4): 379-382. Ouyang X, Yan H H, Liu J K, et al. Nano-titanium dioxide synthesis using gaseous detonation[J]. Chinese Journal of High Pressure Physics, 2007, 21(4): 379-382. (in Chinese)
[8]	Johannessen T, Pratsinis S E, Livbjerg H. Computational fluid-particle dynamics for the flame synthesis of alumina particles[J]. Chem Eng Sci, 2000, 55(1): 177-191.
[9]	陈石, 谢洪勇, 王利希, 等.燃烧法合成TiO₂纳米颗粒的数值模拟[J].大连理工大学学报, 2005, 45(3): 340-345. Chen S, Xie H Y, Wang X L, et al. Simulation of titania nanoparticle synthesis in flame[J]. Journal of Dalian University of Technology, 2005, 45(3): 340-345. (in Chinese)
[10]	Koch W, Friedlander S K. The effect of particle coalescence on the surface area of a coagulating aerosol[J]. J Colloid Interface Sci[J]. 1990, 140(2): 419-427.
[11]	Kobata A, Kusakabe K, Morooka S. Growth and transformation of TiO₂ crystallites in aerosol reactor[J]. Aiche J, 1991, 37(3): 347-359. doi: 10.1002/aic.690370305
[12]	Qu Y D, Li X J, Zhao Z, et al. Synthesis of Sr₂Al₂₄: Er²⁺, Dy³⁺ Nanometer phosphors by detonation and combustion method[J]. Chinese Journal of High Pressure Physics, 2008, 22(2): 175-180.
[13]	Luo N, Li X J, Fei H L, et al. Detonation synthesis of carbon-encapsulated nickel nanoparticles[J]. Chinese Journal of High Pressure Physics, 2011, 25(2): 111-117.
[14]	闫鸿浩, 席树雄, 李晓杰, 等.不同前驱体相对摩尔量对气相爆燃制备纳米SiO2的影响[J].高压物理学报, 2012, 26(6): 627-631. Yan H H, Xi S X, Li X J, et al. Study on the influence of gaseous deflagration preparing nano-SiO₂ with different relative mole amounts of precursor[J]. Chinese Journal of High Pressure Physics, 2012, 26(6): 627-631. (in Chinese)
[15]	Spurr R A, Myers H. Quantitative analysis of anatase-rutile mixtures with X-ray diffratometer[J]. Anal Chem, 1957, 29(5): 760-762. doi: 10.1021/ac60125a006
[16]	奥尔连科.爆炸物理学[M].孙承纬, 译.第3版.北京: 科学出版社, 2011. Орленко Л П. Explosion Physics[M]. Translated by Sun C W. 3rd ed. Beijing: Science Press, 2011. (in Chinese)
[17]	欧阳欣.气相爆燃和爆轰法制备纳米TiO₂颗粒研究[D].大连: 大连理工大学, 2009. Ouyang X. Research synthesis of titanium dioixde nanoparticles by gas-phase deflagration and detonation method[D]. Dalian: Dalian University of Technology, 2009. (in Chinese)