PELE弹丸壳体的损伤断裂模型

梁民族; 李翔宇; 覃金贵; 卢芳云; 王马法

doi:10.11858/gywlxb.2014.06.011

PELE弹丸壳体的损伤断裂模型

doi: 10.11858/gywlxb.2014.06.011

国防科学技术大学理学院工程物理研究所，湖南长沙 410073

基金项目: 国家自然科学基金(11132012)

详细信息

作者简介:
梁民族(1989—), 男，博士研究生，主要从事材料动态力学性能研究.E-mail:mzliang@nudt.edu.cn

通讯作者:
卢芳云(1963—), 女，博士，教授，主要从事材料动态力学性能研究.E-mail:fylu@nudt.edu.cn

中图分类号: O346.1
计量
- 文章访问数: 6776
- HTML全文浏览量: 2107
- PDF下载量: 286
出版历程
- 收稿日期: 2012-11-30
- 修回日期: 2013-02-22

Damage and Fracture Model for Shell of PELE

Institute of Engineering Physics, College of Science, National University of Defense Technology, Changsha 410073, China

摘要

摘要: 结合横向效应增强型侵彻体(PELE)侵彻金属靶板的数值模拟结果和实验结果，将PELE弹丸壳体膨胀断裂过程分为加速膨胀和匀速膨胀两个阶段。在封加波提出的损伤度模型的基础上，推导得到PELE弹丸壳体的损伤断裂方程；并通过PELE壳体断裂实例计算了PELE弹丸壳体膨胀断裂过程的参数，分析了弹丸着靶速度与壳体断裂之间的关系，为PELE弹丸设计提供了理论指导。
- 横向效应增强型侵彻体 /
- 壳体 /
- 横向效应 /
- 损伤断裂 /
- 临界应变
Abstract: Combining the simulation with the experimental results of the penetration process of penetrator with enhanced lateral effect (PELE) in metallic target, the process of the shell expansion can be divided into two stages, the accelerating expansion and the uniform expansion.Based on the model of the damage function by Feng Jiabo, we obtained the damage and fracture evolution equation responsible for the shell of PELE.According to the damage evolution equation responsible for the shell of PELE, the fracture process parameters of PELE were calculated.Moreover, the relationship between shell fracture critical strain and velocity of the projectile was analysised, which is useful in engineering design of PELE.
- penetrator with enhanced lateral effect /
- shell /
- lateral effect /
- damage and fracture /
- critical strain

HTML全文

1. 引言

自1996年German-French Research Institute Saint Louis (ISL)实验室第一次提出横向效应增强型侵彻体(Penetrator with Enhanced Lateral Effect, PELE)概念以来, 国内外学者对PELE弹丸的作用过程进行了广泛研究。在PELE弹丸壳体断裂的机理方面, Kesberg等人^[1]认为壳体侵彻目标的内核因密度较低而被压缩并沿径向膨胀, 导致壳体内壁压力剧增至吉帕级, 弹丸穿透目标后能量瞬间释放, 导致壳体破裂成大量破片。Paulus等人^[2]结合Recht-Ipson模型^[3]和Mott模型^[4]计算出弹体的剩余速度、装填物的压力以及壳体破片的径向飞散速度, 并且用弱激波理论描述了PELE弹丸壳体的断裂过程。对于PELE弹丸壳体断裂的研究, 除了可从力学和能量的角度定性地解释PELE弹丸壳体断裂过程外, 还可以从损伤断裂的角度, 具体分析其在侵彻过程中的断裂机理。

在研究材料动态拉伸断裂方面有许多模型, Seaman、Curran和Shockey^[5]从实验出发, 基于微损伤的统计性分析结果, 提出了成核与长大模型(Nucleation and Growth, NAG)。但是NAG模型计算需要大量的实验参数, 实用性比较差。封加波等人^[6-7]在NAG模型的基础上利用单孔洞近似, 从能量平衡的角度出发, 提出了简单实用的损伤度函数模型。本研究基于损伤度模型, 结合PELE弹丸侵彻过程, 将PELE弹丸壳体的膨胀断裂过程分为加速膨胀和匀速膨胀两个阶段, 推导出这两个阶段PELE弹丸壳体的损伤断裂方程, 并根据损伤断裂方程分析影响PELE弹丸横向效应的内在机理。

2. 金属壳体动态损伤模型

2.1 金属壳体的动态本构关系

PELE弹丸壳体一般为高密度金属或合金。金属或合金材料在高应变率下的变形过程比较复杂, 理论上通常把动态变形过程划分为几个阶段, 如弹性阶段、塑性阶段和失效阶段, 对不同变形阶段需要用不同的本构关系表达式进行描述。动态塑性本构方程可以写为

$\sigma=\varphi\left(e^{\mathrm{p}}, \dot{e}^{\mathrm{p}}\right)$

(1)

式中:σ为材料的动态屈服应力, e^p为径向塑性自然应变, 为径向塑性自然应变率。

根据文献[7], 金属壳体的动态本构关系可以表示为

$\sigma=\sigma_{0}+K e^{\mathrm{p}}+\eta \dot{e}^{\mathrm{p}}$

(2)

式中:σ₀为静态屈服强度, K为材料强化系数, η为材料黏度系数。

对于柱壳结构有

$e^{\mathrm{p}}=\ln \left(\frac{R(t)}{R_{0}}\right)$

(3)

$\dot{e}^{\mathrm{p}}=u(t) / R(t)$

(4)

$\varepsilon^{\mathrm{p}}=\frac{R(t)-R_{0}}{R_{0}}$

(5)

式中:R₀为壳体初始半径, R(t)为壳体实时半径, R₀、R(t)均是壳体内径和外径的平均值, ε^p为径向塑性应变, u(t)为壳体径向膨胀速度。结合(3)式和(5)式可以得到e^p与ε^p的关系

$e^{\mathrm{p}}=\ln \left(1+\varepsilon^{\mathrm{p}}\right)$

(6)

将(6)式代入(2)式, 可以将动态本构关系改写成以下形式

$\sigma=\sigma_{0}+K \ln \left(1+\varepsilon^{\mathrm{P}}\right)+\eta \dot{e}^{\mathrm{p}}$

(7)

2.2 金属壳体的动态损伤模型

本研究所采用的断裂准则建立在封加波提出的损伤度模型的基础上。金属材料的损伤度包括在应力波作用下材料初始损伤缺陷及其发展, 以及新产生的损伤缺陷及其发展, 而且材料的损伤度具有累积效应。在PELE弹丸壳体动态断裂的过程中, 为了考虑材料的损伤累积效应, 引入损伤变量D(t), D(t)定义为材料某一截面上微孔洞所占的面积比。参照文献[6], 有如下形式的方程

$\frac{\mathrm{d} D}{\mathrm{d} t}=\frac{\left[(1-D)\left(\sigma-\sigma_{0}\right)\right]^{2}}{\eta K}$

(8)

求解方程(8)式需要知道σ(或ε^p和随时间变化的规律。从(4)式和(5)式看出, 需要知道壳体膨胀的实时半径R(t)和壳体径向膨胀速度u(t)的函数形式。在处理实际问题时, 很难求出解析表达式, 一般需要结合实验结果求解。

3. PELE弹丸壳体膨胀规律

3.1 PELE作用机理

PELE弹丸是一种基于物理效应、不需要装填炸药和引信的新概念弹药, 主要用于防空、反导、城市作战等领域。PELE弹丸由壳体和内核组成, 壳体一般为密度较大的金属材料, 内核是密度及强度比较低的金属或聚合物。高密度金属壳体对靶板具有良好的侵彻性能, 而内核材料在侵彻过程中被封闭压缩, 巨大的压力在内核中迅速积聚, 弹丸穿透靶板后能量瞬间释放导致外壳破裂解体。

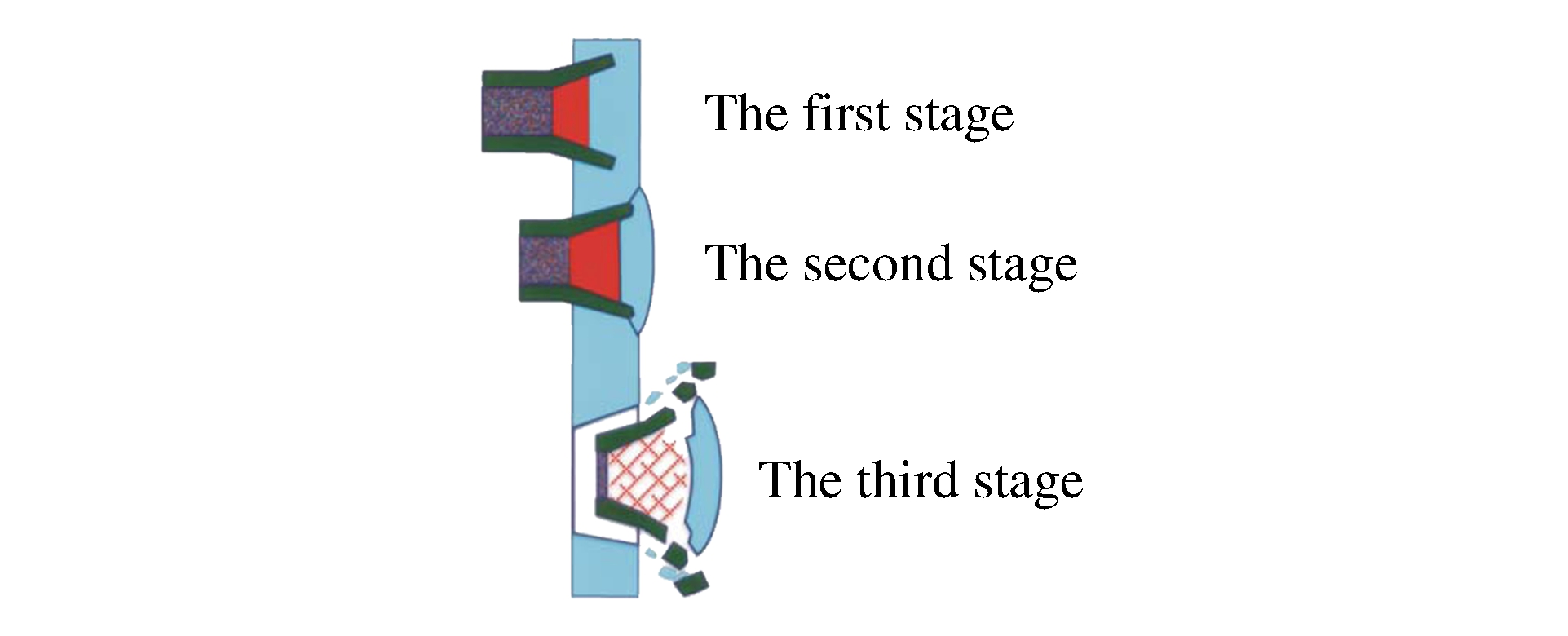
PELE的横向增强效应作用过程分为3个主要时段和一个后效作用时段^[1]。如图 1所示, 第1时段, 当弹丸击中目标后, 外层高密度壳体侵彻目标, 内核因材料强度低而无法侵彻, 将会在靶前停滞而被压缩; 第2时段, 封闭压缩过程中产生的高压将使内核材料沿径向膨胀, 导致壳体内壁压力急剧增加, 可达到数吉帕; 第3时段, 当应力应变达到壳体的破坏极限时, 出靶后的卸载应力波致使外层弹体破裂成大小不同的破片。后效作用时段则是壳体破片的径向飞散以及内核和塞块间继续相互作用的过程。

图 1 PELE的3个阶段

Figure 1. Three stages of penetration process of the PELE

下载: 全尺寸图片幻灯片

3.2 PELE侵彻过程数值计算

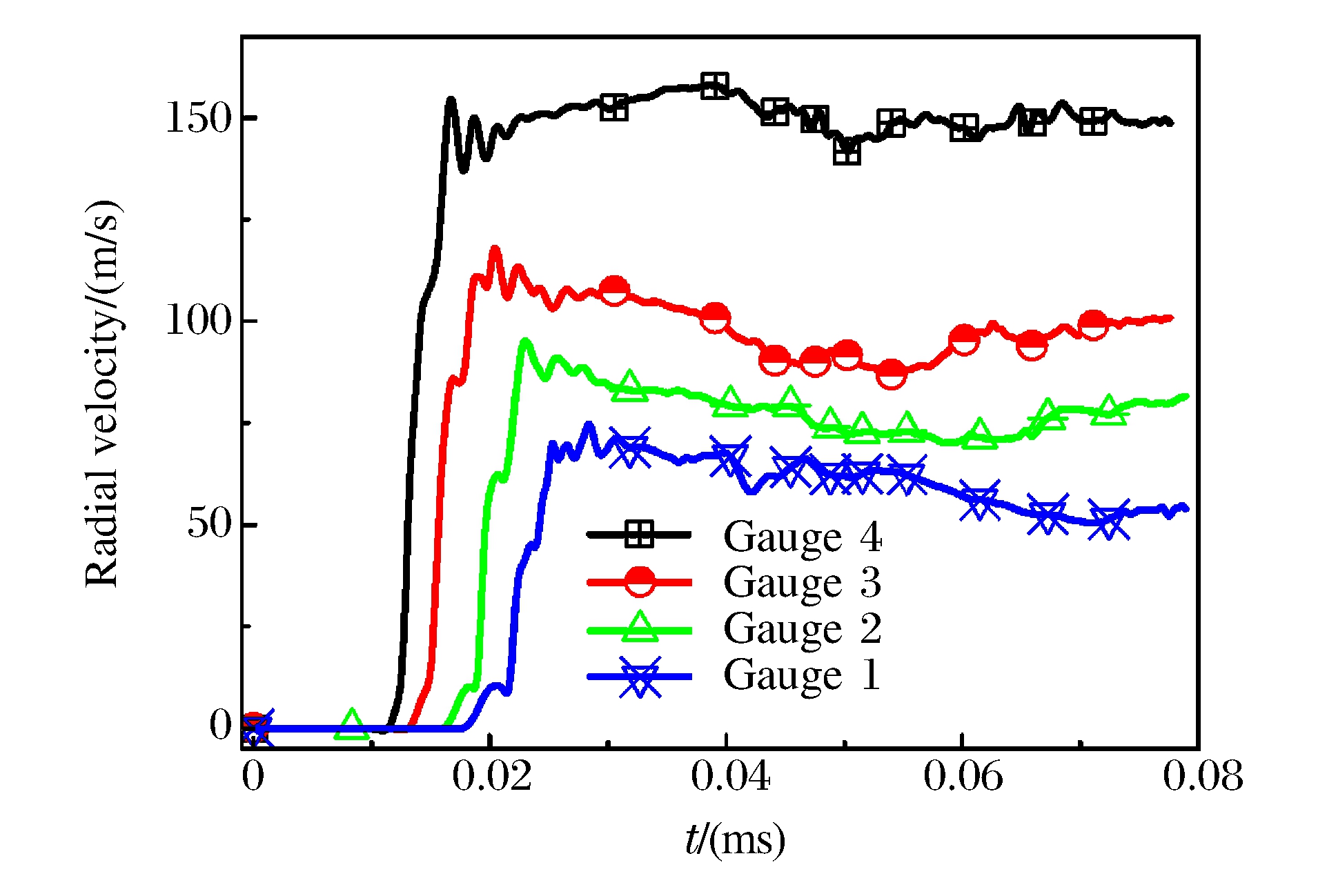
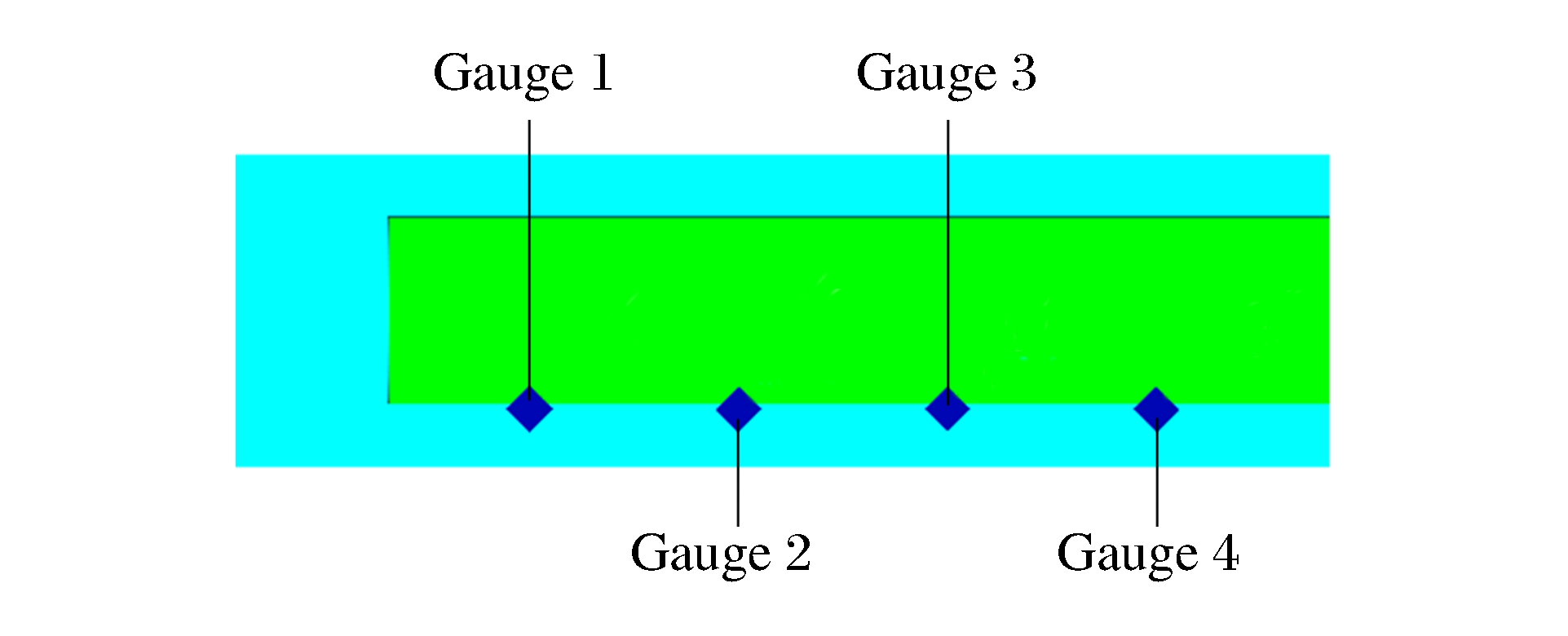
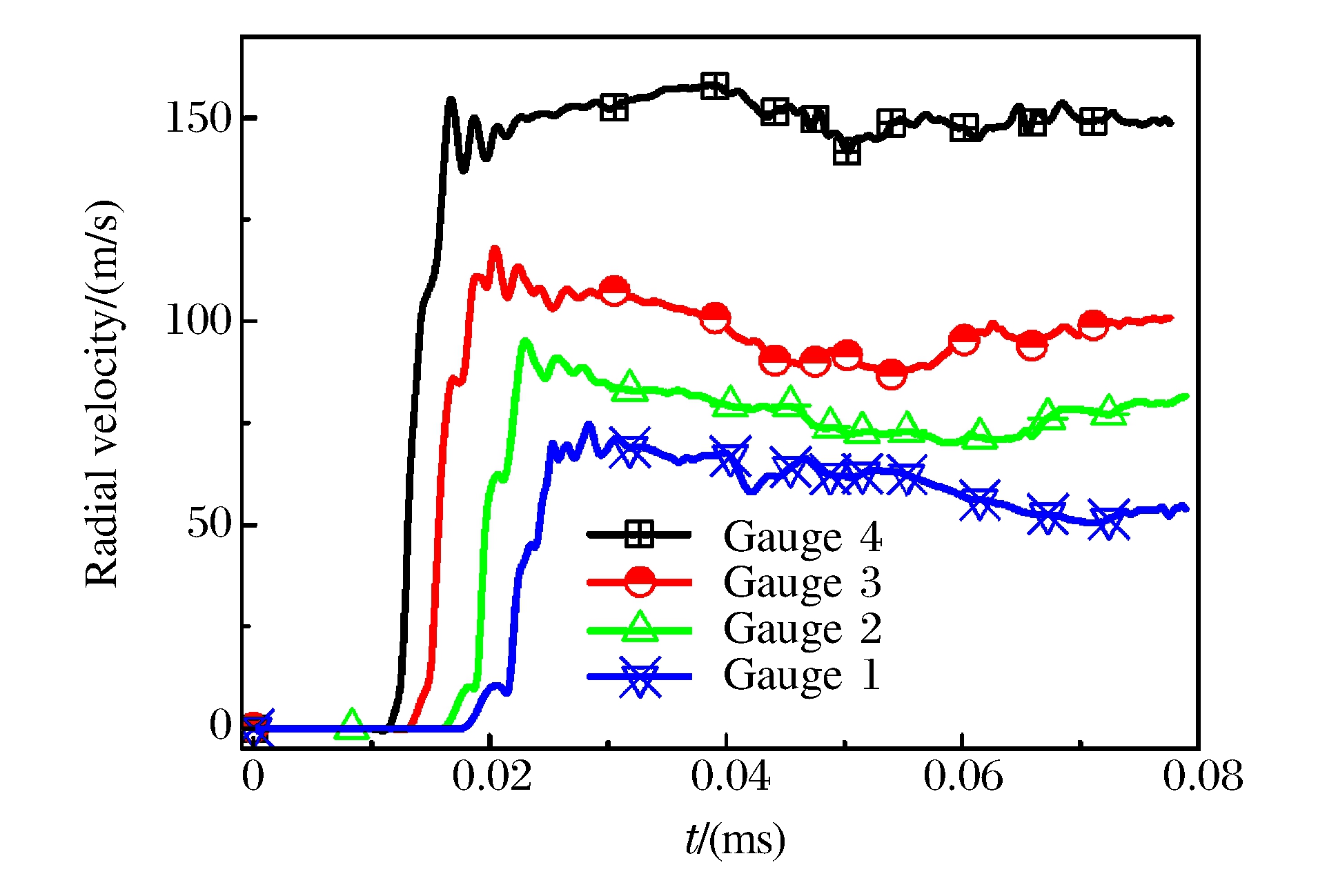
图 2给出了PELE弹丸计算模型, 其中壳体材料为35CrMnSi, 长度为105 mm, 外径为30 mm, 内径为18 mm, 弹底部厚为15 mm; 内核材料为聚乙烯, 长度为90 mm, 直径为18 mm; 靶板材料为装甲钢, 厚度为8 mm。网格平均尺寸为壳体1 mm, 内核1.2 mm, 靶板采用变步长网格(0.5~10 mm)以提高计算效率。为了获得侵彻过程中的时间历程参数, 在弹丸模型的壳体中心线沿轴向均匀分布4个观测点(Gauge点), 每个观测点间隔20 mm, 如图 2所示。

图 2 PELE弹丸计算模型

Figure 2. Calculation model of the PELE

下载: 全尺寸图片幻灯片

表 1、表 2分别为材料模型和材料参数。数值计算采用拉格朗日方法, 材料均采用侵蚀算法, 靶板采用材料应变失效模型, 壳体使用有效应力失效模型。采用Stochastic模型^[8]模拟壳体随机断裂, 其中材料弱化点的破坏概率在[0, 1]范围为

表 1 材料模型

Table 1. Material model

Component	Material species	Equation of state	Strength model	Invalidation model
Shell	35CrMnSi	Linear	Johnson-Cook	Principal stress
Core	Polyethylene	Shock	von-Mises	-
Target plate	RHA	Shock	von-Mises	Material strain

下载: 导出CSV

| 显示表格

表 2 材料参数

Table 2. Material parameters

Material	ρ/(g/cm³)	E/(GPa)	σ/(MPa)	G/(GPa)	ν
35CrMnSi	7.8	210	1 270	81	0.33
Polyethylene	0.94	1.5	0.26	0.55	0.45
RHA	7.8	171	1400	64.1	0.33

下载: 导出CSV

| 显示表格

$P=1-\exp \left(-c \mathrm{e}^{\gamma \varepsilon} / \gamma\right)$

(9)

式中:P为应变为ε时的网格破坏概率, c、γ取决于材料性质, 根据文献[8], 取c=0.467, γ=10。

PELE弹丸以700 m/s的着靶速度垂直侵彻8 mm厚的装甲钢靶板。壳体中Gauge点沿壳体径向速度变化曲线如图 3所示。从图 3中看出, PELE侵彻过程第2时段, 壳体径向先经历短暂加速膨胀阶段, 膨胀速度达到一个较大值; PELE侵彻过程第3时段, 壳体膨胀速度小幅震荡并趋于稳定。

图 3 PELE弹丸壳体Gauge点的径向速度

Figure 3. The radical velocity of gauge points in the PELE

下载: 全尺寸图片幻灯片

3.3 实验过程与结果

PELE实验弹丸参数:外径为30 mm, 内径为18 mm, 长度为105 mm; 壳体材料采用35CrMnSi合金钢, 内核为聚乙烯, 长度为90 mm, 靶板为装甲钢, 厚度为8 mm; 装配全弹质量为350 g。

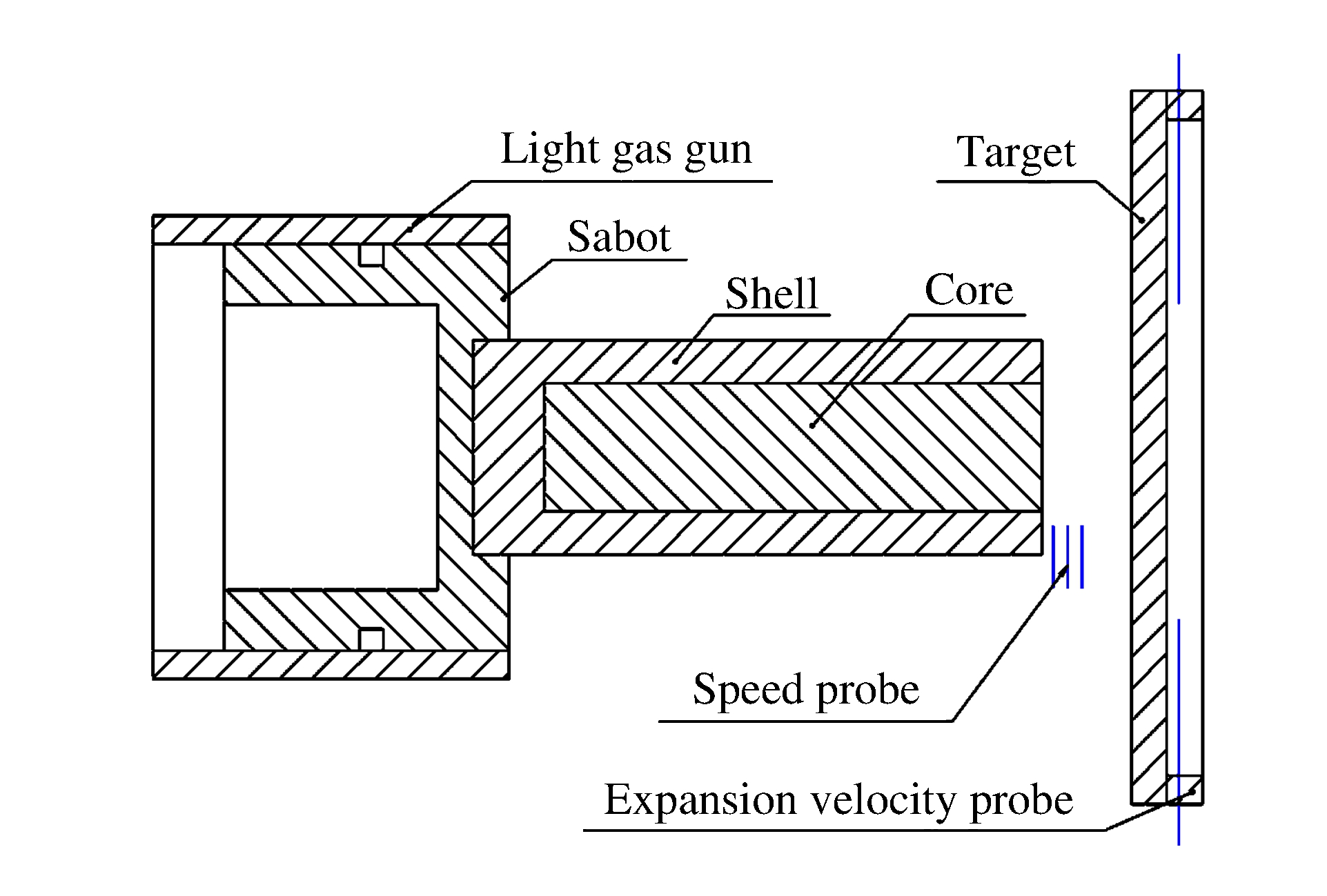
实验弹采用轻气炮发射。弹丸着靶和出靶分别设置了测速点探针, 以测量着靶速度和弹丸穿透靶板的时间。为了获得弹丸头部出靶时的膨胀速度, 设计了一套环形电探针测量装置。实验装置示意图如图 4所示, 实验装置各部分如图 5所示。

图 4 实验装置示意图

Figure 4. Experimental setup

下载: 全尺寸图片幻灯片

图 5 实验装置

Figure 5. Experimental device

下载: 全尺寸图片幻灯片

表 3分别统计了3发有效实验的弹丸着靶速度、弹丸头部从着靶到出靶的穿靶时间, 以及出靶时弹丸头部的径向速度。应该指出的是, 由于弹丸穿靶时间极短, 弹丸出靶时头部的径向速度比较大, 探针测试存在一定的误差。

表 3 着靶速度与穿靶时间统计

Table 3. Statistics of the impact velocity and the penetrating time

Experimental No.	Velocity/(m/s)	Time/(μs)	Radical velocity/(m/s)
1	643	8.4	127
2	694	7.2	142
3	762	6.5	153

下载: 导出CSV

| 显示表格

3.4 PELE侵彻过程壳体的膨胀规律

壳体膨胀断裂主要处于PELE侵彻过程的第2时段和第3时段。壳体动态断裂过程可以描述为:应力波从内核传入壳体内壁, 壳壁开始加速膨胀, 在应力波多次反射效应下膨胀速度振荡衰减, 直至最终趋于平稳。其衰减规律基本上按余弦函数变化^[9-10], 所以径向速度公式可以写为

$u(t)=\left\{\begin{array}{ll} C t & t_{0} \leqslant t \lt t_{1} \\ A \mathrm{e}^{-\lambda t} \cos (\psi t)+u_{0} & t_{1} \leqslant t \lt t_{c} \end{array}\right.$

(10)

式中:A、ψ、C、λ为与总体模型有关的参数, u₀为稳态时的径向速度值。t₀为应力波传到壳体外壁的时刻, t₁为壳体膨胀加速结束的时刻, t_c为壳体发生贯穿性断裂的时刻。

根据侵彻过程壳体的膨胀规律, 可以将PELE壳体断裂过程分为壳体加速膨胀阶段和壳体匀速膨胀阶段。调整数值模拟中弹丸的着靶速度, 使其工况与3发实验相吻合, 对比数值模拟结果与实验结果发现, PELE壳体加速膨胀的时间与壳体从着靶到出靶的时间相吻合。可以看出当壳体处于靶板内时, 壳体处于加速状态; 当壳体出靶后, 壳体匀速膨胀。

4. PELE弹丸壳体断裂过程求解

根据PELE侵彻过程壳体的膨胀规律, 将PELE壳体断裂过程分为两个阶段:壳体加速膨胀阶段和壳体匀速膨胀阶段。

第1阶段:壳体加速膨胀阶段。假定自然应变率可以近似看作常数

$\dot{e}^{\mathrm{p}}=u(t) / R(t)=c$

(11)

另外

$\mathrm{d} t=\mathrm{d} e^{\mathrm{p}} / \dot{e}^{\mathrm{p}}$

(12)

对(12)式积分得

$t_{1}-t_{0}=e_{1}^{\mathrm{p}} / \dot{e}^{\mathrm{p}}$

(13)

将(7)代入(8), 在[t₀, t₁]内积分得

$D_{1}=1-\frac{3 \omega_{1}}{\left(\omega_{1}+e_{1}^{\mathrm{p}}\right)^{3}+3 \omega_{1}-\omega_{1}^{3}}$

(14)

式中:D₁为t₁时刻的损伤度。(14)式中

$\omega_{1}=(K / \eta) \dot{e}^{\mathrm{p}}$

(15)

通过实验结果可以得到代入(13)式可以求出将代入(14)式求出D₁。

第2阶段:壳体匀速膨胀阶段。第1阶段结束时刻即为第2阶段初始时刻。依据PELE壳体膨胀规律, 给出描述壳体膨胀速度的变化规律为

$u(t)=A \mathrm{e}^{-\lambda t} \cos (\psi t)+u_{0}$

(16)

(16) 式反映应力波多次反射引起的衰减振荡, 代表了壳体膨胀速度的真实情况, 但直接代入损伤度方程难以求解。为了方便积分, 这里按照能量等效原理取均值, 假设柱壳膨胀速度u(t)等于常数

$u(t)=u_{0}$

(17)

由于

$\begin{aligned} \dot{e}^{\mathrm{p}} =u(t) / R(t) \end{aligned}$

(18)

$\begin{aligned} \dot{e}_{2}^{\mathrm{p}} & =u(t) / R_{2} \end{aligned}$

(19)

$\begin{aligned} \\ u(t) & =\mathrm{d} R(t) / \mathrm{d} t \end{aligned}$

(20)

将(5)式、(18)式、(19)式代入(20)式, 得

$\mathrm{d} t=\mathrm{d} R(t) / u(t)=\mathrm{d} \varepsilon^{\mathrm{p}} / \dot{e}_{2}^{\mathrm{p}}$

(21)

式中: 为第2阶段的初始径向塑性自然应变率, R₂为第2阶段壳体的初始半径。

将(7)式、(17)式、(21)式代入(8)式, 在[t₁, t_c]积分得

$\int_{D_{1}}^{D_{c}} \frac{\mathrm{d} D}{(1-D)^{2}}=\int_{\varepsilon_{1}^{\mathrm{p}}}^{\varepsilon_{\mathrm{c}}^{\mathrm{p}}} \frac{1}{\omega_{2}}\left[\ln \left(1+\varepsilon^{\mathrm{p}}\right)+\frac{\omega_{2}}{1+\varepsilon^{\mathrm{p}}}\right] \mathrm{d} \varepsilon^{\mathrm{p}}$

(22)

式中: 为壳体发生贯穿性破坏的损伤度。经过整理, 最终得

$\begin{array}{l} \frac{\varepsilon_{\mathrm{c}}^{\mathrm{p}}-\varepsilon_{1}^{\mathrm{p}}}{\left(1+\varepsilon_{\mathrm{c}}^{\mathrm{p}}\right)\left(1+\varepsilon_{1}^{\mathrm{p}}\right)} \omega_{2}^{2}+\left[\left(e_{\mathrm{c}}^{\mathrm{p}}\right)^{2}-\left(e_{1}^{\mathrm{p}}\right)^{2}-\frac{D_{\mathrm{c}}-D_{1}}{\left(1-D_{\mathrm{c}}\right)\left(1-D_{1}\right)}\right] \omega_{2}+ \\ \left(1+\varepsilon_{\mathrm{c}}^{\mathrm{p}}\right)\left[\left(e_{\mathrm{c}}^{\mathrm{p}}\right)^{2}-2 e_{\mathrm{c}}^{\mathrm{p}}+2\right]-\left(1+\varepsilon_{1}^{\mathrm{p}}\right)\left[\left(e_{1}^{\mathrm{p}}\right)^{2}-2 e_{1}^{\mathrm{p}}+2\right]=0 \end{array}$

(23)

式中: 为第一阶段壳体材料径向塑形应变。由(6)式知与满足以下关系式

$e_{1}^{\mathrm{p}}=\ln \left(1+\varepsilon_{1}^{\mathrm{p}}\right)$

(24)

(23) 式为PELE弹丸壳体的损伤断裂方程。第1阶段的自然应变率和第2阶段的初始半径R₂、径向速度u₀可以通过实验得到, 通过R₂和u₀可以求出而壳体材料参数σ₀、K、η和D_c均可以通过查找手册和文献获得, 最终可以得到一个确定的临界应变作为损伤断裂判据。

将(17)式、(19)式代入(21)式, 在[t₁, t_c]内积分可得壳体发生贯穿断裂的时刻t_c

$t_{\mathrm{c}}-t_{1}=R_{2}\left(\varepsilon_{\mathrm{c}}^{\mathrm{p}}-\varepsilon_{1}^{\mathrm{p}}\right) / u_{0}$

(25)

5. PELE壳体断裂实例

对于35CrMnSi, 参照文献[10], 壳体特征参数取η=-12 kPa·s, K=1.66 GPa, ω_λ=3.5 kJ/m², D₀=10^-5, D_c=0.2, σ₀=0.72 GPa。当初始半径R₀=15 mm的PELE弹丸以1 km/s速度着靶时, 结合实验数据, 得到第1阶段的自然应变率和第2阶段的初始半径R₂及径向膨胀速度u₀, 见表 4。

表 4 3个时刻膨胀断裂过程的参数

Table 4. Parameters of expansion and fracture at three time points

t/(μs)	$\dot{e}^{\mathrm{p}} /\left(10^{4} \mathrm{~s}^{-1}\right)$	R₂/(mm)	u₀/(m/s)
8.4	2.62	17.7	127
7.2	1.91	18.6	142
6.5	1.71	19.9	153

下载: 导出CSV

| 显示表格

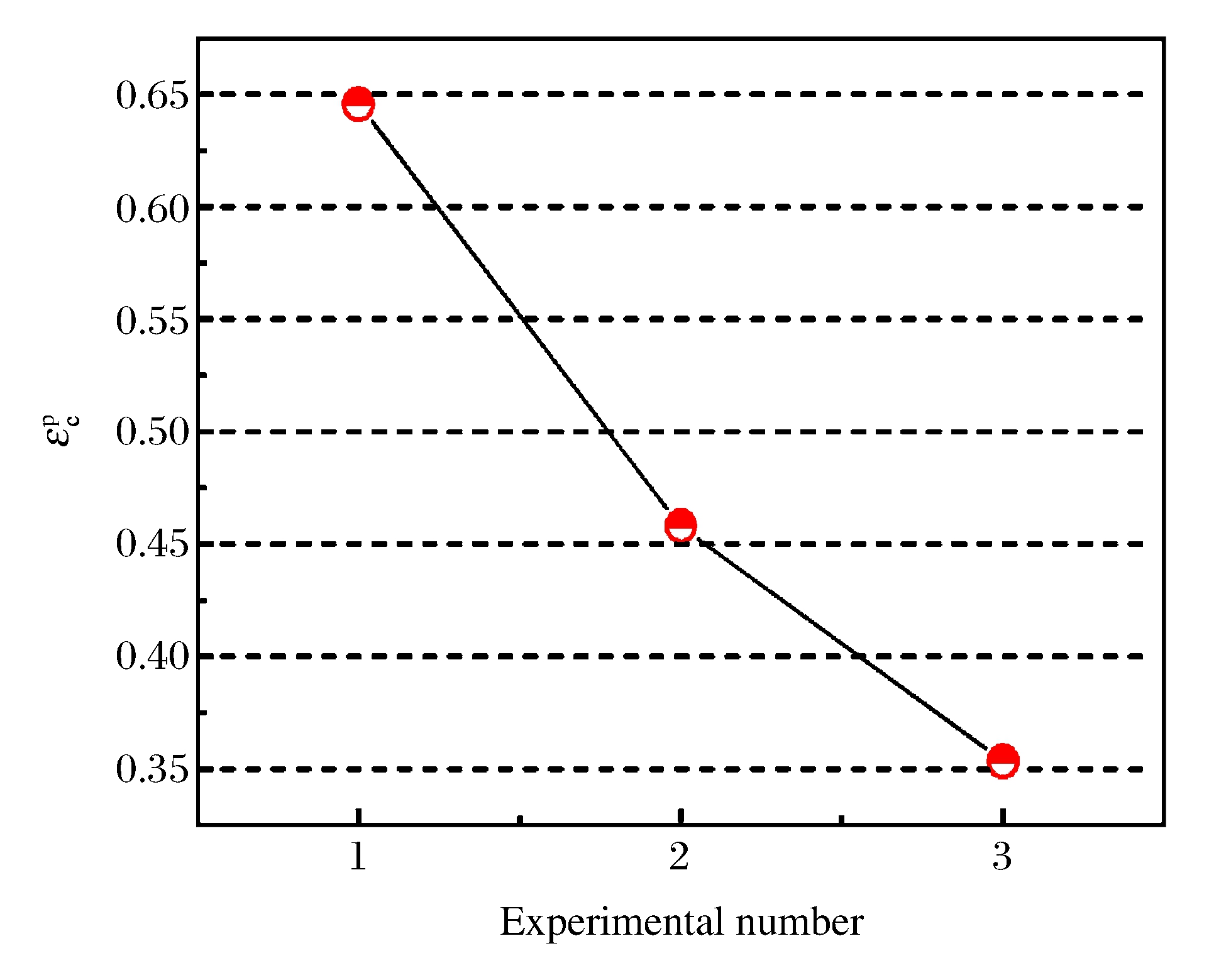
将第2阶段的初始半径R₂及径向膨胀速度u₀代入(19)式, 得到第2阶段的初始应变率将第一阶段代入(13)式可以求出将代入(14)式求出D₁; 同时将代入(24)式求出将代入(23)式, 得到3个典型时刻临界应变如图 6所示。从图 6中可以看出, 在一定速度范围内, 随着弹丸着靶速度的增加, 壳体断裂的临界应变明显降低。

图 6 PELE壳体断裂的临界应变

Figure 6. Critical strain of the PELE

下载: 全尺寸图片幻灯片

6. 结论

(1) PELE弹丸在侵彻过程中壳体膨胀断裂可以分为加速膨胀和匀速膨胀两个阶段, 在封加波提出的损伤度模型的基础上, 得到了PELE弹丸壳体的损伤断裂方程和断裂判据。

(2) 根据PELE弹丸壳体损伤断裂方程, 计算出PELE弹丸壳体膨胀断裂过程的参数, 分析了弹丸着靶速度与壳体断裂之间的关系, 可为PELE弹丸设计提供理论指导。

致谢: 感谢胡玉涛博士和曹雷博士在公式推导和实验方面给予的帮助。

图 1 PELE的3个阶段

Figure 1. Three stages of penetration process of the PELE

下载: 全尺寸图片幻灯片

图 2 PELE弹丸计算模型

Figure 2. Calculation model of the PELE

下载: 全尺寸图片幻灯片

图 3 PELE弹丸壳体Gauge点的径向速度

Figure 3. The radical velocity of gauge points in the PELE

下载: 全尺寸图片幻灯片

图 4 实验装置示意图

Figure 4. Experimental setup

下载: 全尺寸图片幻灯片

图 5 实验装置

Figure 5. Experimental device

下载: 全尺寸图片幻灯片

图 6 PELE壳体断裂的临界应变

Figure 6. Critical strain of the PELE

下载: 全尺寸图片幻灯片

表 1 材料模型

Table 1. Material model

Component	Material species	Equation of state	Strength model	Invalidation model
Shell	35CrMnSi	Linear	Johnson-Cook	Principal stress
Core	Polyethylene	Shock	von-Mises	-
Target plate	RHA	Shock	von-Mises	Material strain

下载: 导出CSV

表 2 材料参数

Table 2. Material parameters

Material	ρ/(g/cm³)	E/(GPa)	σ/(MPa)	G/(GPa)	ν
35CrMnSi	7.8	210	1 270	81	0.33
Polyethylene	0.94	1.5	0.26	0.55	0.45
RHA	7.8	171	1400	64.1	0.33

下载: 导出CSV

表 3 着靶速度与穿靶时间统计

Table 3. Statistics of the impact velocity and the penetrating time

Experimental No.	Velocity/(m/s)	Time/(μs)	Radical velocity/(m/s)
1	643	8.4	127
2	694	7.2	142
3	762	6.5	153

下载: 导出CSV

表 4 3个时刻膨胀断裂过程的参数

Table 4. Parameters of expansion and fracture at three time points

t/(μs)	$\dot{e}^{\mathrm{p}} /\left(10^{4} \mathrm{~s}^{-1}\right)$	R₂/(mm)	u₀/(m/s)
8.4	2.62	17.7	127
7.2	1.91	18.6	142
6.5	1.71	19.9	153

下载: 导出CSV

参考文献(11)

[1]	Kesberg G, Schirm V, Kerk S. PELE-the future ammunition concept[C]//21st international Symposium on Ballistics. Adelaide, Australia, 2004: 1134-1144.
[2]	Paulus G, Schirm V. Impact behavior of PELE projectiles perforating thin target plates[J]. Int J Impact Eng, 2006, 33(1): 1134-1144.
[3]	Recht R, Ipson T. Ballistic perforation dynamics[J]. J Appl Mech, 1963, 30(3): 384-390. doi: 10.1115/1.3636566
[4]	Mott N F. Fragmentation of shell casings and the theory of rupture in metals[M]//Fragmentation of Rings and Shells. Berlin/Heidelberg: Springer-Verlag, 2006: 295-325.
[5]	Seaman L, Curran D R, Shockey D A. Computational models for ductile and brittle fracture[J]. J Appl Phys, 1976, 47(11): 4814-4826. doi: 10.1063/1.322523
[6]	封加波, 经福谦, 苏林祥, 等.对薄层柱壳爆炸膨胀断裂过程的研究[J].高压物理学报, 1988, 2(2): 97-103. Feng J B, Jing F Q, Su L X, et al. Studies of the explosion expanding-fracture process of a thin cylindrical shell[J]. Chinese Journal of High Pressure Physics, 1988, 2(2): 97-103. (in Chinese)
[7]	Feng J, Jing F, Zhang G, et al. Dynamic ductile fragmentation and the damage function model[J]. J Appl Phys, 1997, 81(6): 2575-2578. doi: 10.1063/1.363921
[8]	蒋建伟, 张谋, 门建兵, 等. PELE弹侵彻过程壳体膨胀破裂的数值模拟[J].计算力学学报, 2009, 26(4): 568-572. Jiang J W, Zhang M, Men J B, et al. 3D simulation of expanding motion and fracture of ductile metal ring[J]. Chinese Journal of Computational Mechanics, 2009, 26(4): 568-572. (in Chinese)
[9]	Haghpanah Jahromi B, Vaziri A. Instability of cylindrical shells with single and multiple cracks under axial compression[J]. Thin-Walled Struct, 2012, 54: 35-43. doi: 10.1016/j.tws.2012.01.014
[10]	Fu J, To C W S. Bulging fractor and geometrically nonlinear responses of cracked shell structures under internal pressure[J]. Eng Struct, 2012, 41: 456-463. doi: 10.1016/j.engstruct.2012.04.001
[11]	荆秀芝, 陈文, 杨武明.金属材料应用手册[M].西安: 陕西科学技术出版社, 1989. Jing X Z, Chen W, Yang W M. Application Manal for Metal Material[M]. Xi'an: Shanxi Science and Technology Publishing House, 1989. (in Chinese)