Simulation of Expansion of High Pressure Bubble under Water in Complex Calculation Region using NGFM in Cartesian Coordinate System
-
摘要: 采用NGFM(New version of Ghost Fluid Method)处理复杂计算域的固壁边界，用RGFM(Real Ghost Fluid Method)求解气-水界面附近网格节点的状态参数，从而在直角坐标系下对复杂计算域的水下高压气泡膨胀问题进行数值模拟。流场控制方程选用Euler方程，用五阶WENO格式离散空间导数项，二阶Runge-Kutta法离散时间导数项；气-水界面追踪使用Level Set方法，对Level Set方程，用五阶HJ-WENO(Hamilton-Jacobi WENO)和三阶Runge-Kutta法求解。将计算结果与任意坐标系下的结果进行对比，验证了NGFM在笛卡尔网格中处理复杂形状固壁边界的可行性。得到了水下流场压力等值线图、高压气泡的演变过程以及特定点处的压力-时间曲线。计算结果表明，高压气泡在固壁反射激波的作用下，膨胀过程受到抑制；强激波在固壁的反射会导致固壁附近出现大范围的空化流动。
-
关键词:
- 高压气泡膨胀 /
- 任意坐标系 /
- 复杂计算域 /
- Level Set方法 /
- Ghost Fluid方法
Abstract: We adopted a new version of ghost fluid method (NGFM) to treat the wall boundary in a complex calculation region in Cartesian coordinate system, and real ghost fluid method (RGFM) to predict the flow states at grid nodes just next to the gas-liquid interface.Flow field was solved by Euler equation with 5th-order WENO spatial discretization and 2nd-order Runge-Kutta (R-K) time discretization.We used the level set method to keep track of gas-liquid interface.Level set function was discretized by 5th-order Hamilton-Jacobi WENO and 3rd-order R-K method.We verified that NGFM was easy to extend and could be applied to treat complex wall boundary in Cartesian grid by comparing with results in arbitrary coordinate system.We carried out pressure contours, the change process of bubble shape and pressure history at some given points.The numerical results demonstrate that the expansion of high pressure bubble is restricted by the reflected shock wave from the wall.It is also shown that the reflection of strong shock wave from wall can lead to extensive cavitation flow. -
1. 引言
水下高压气泡膨胀问题常见于水下爆炸研究。数值模拟此类问题时, 如何精确处理高压力比、高密度比的气-水界面一直是难点。Blake等人[1-2]采用边界元方法(Boundary Element Method, BEM)研究了水下爆炸气泡的演化过程; Liu等人[3-5]用光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)方法对水下爆炸高压气泡的演化进行了一维和二维数值模拟; Vernon等人[6-7]采用Laplace方程描述速度场, 研究气泡运动。Zhang等人[8]将SPH和BEM耦合, 对柱形装药的水下爆炸进行了数值模拟。
然而, 关于数值模拟复杂计算域中水下高压气泡膨胀问题的文献一直很少, 原因是笛卡尔网格不能很好地处理复杂计算域中的不规则边界。通过建立任意坐标系网格可以解决这个问题, 但是任意坐标系中的数值模拟对网格形状要求较高, 并且引入网格导数会增加计算误差。由Fedkiw提出的NGFM(New Version of Ghost Fluid Method)可以较好地处理流-固边界[9]。本研究将复杂计算域中的壁面拓展为一种固体物质, 以便应用NGFM处理固壁边界条件; 同时, 选用RGFM(Real Ghost Fluid Method)[10]处理气-水界面, 以二维90°弯头为例, 对复杂计算域中的水下高压气泡膨胀问题进行数值模拟, 以期指导工程和实验。
2. 控制方程和数值方法
2.1 Euler方程
流场控制方程采用欧拉方程
∂∂t(ρρuρvρE)+∂∂x[ρuρu2+pρuvu(ρE+p)]+∂∂y[ρvρvuρv2+pv(ρE+p)]=0 (1) 式中:ρ为流体密度; u, v分别为x, y方向的速度; p为流体压力; E为单位质量流体的总能, 且有E=e+(u2+v2)/2, 其中e为单位质量流体的内能。
2.2 状态方程
对于水, 当p≥psat(psat为饱和蒸汽压)时, 采用Tait方程[11]; 当p < psat时, 使用等熵空化流方程[12]
ρ={ρ0[(p+B−A)/B]1/Np⩾psatkρcav g+ρcav 1[(p+B−A)/(pcav +B−A)]−1/N+k(p/pcav )−1/np<psat (2) 式中:
分别为空化组分系数, 空化压力, 气相空化密度和液相空化密度; A=0.1 MPa, B=0.331 GPa, ρ0=1.0 g/cm3, N=7.15, n=1.33。
对于高压气体, 使用γ-Law状态方程(γ为气体绝热指数)
p=ρe(γ−1) (3) 2.3 Level Set方程
气-水界面追踪采用Level Set方程[13]
φt+v⋅∇φ=0 (4) 式中:φ为符号距离函数, v为速度矢量。对于水和高压气体, 需要分别求解φwater和φgas。在计算中固壁不发生移动, 故φwall不需要求解。由于数值方法的内在效应, Level Set方程中的φ在几个时间步的求解后, 就不再满足距离函数的定义, 此时需要用初始化方程对φ重新初始化, 详情可参考文献[14]。
2.4 RGFM
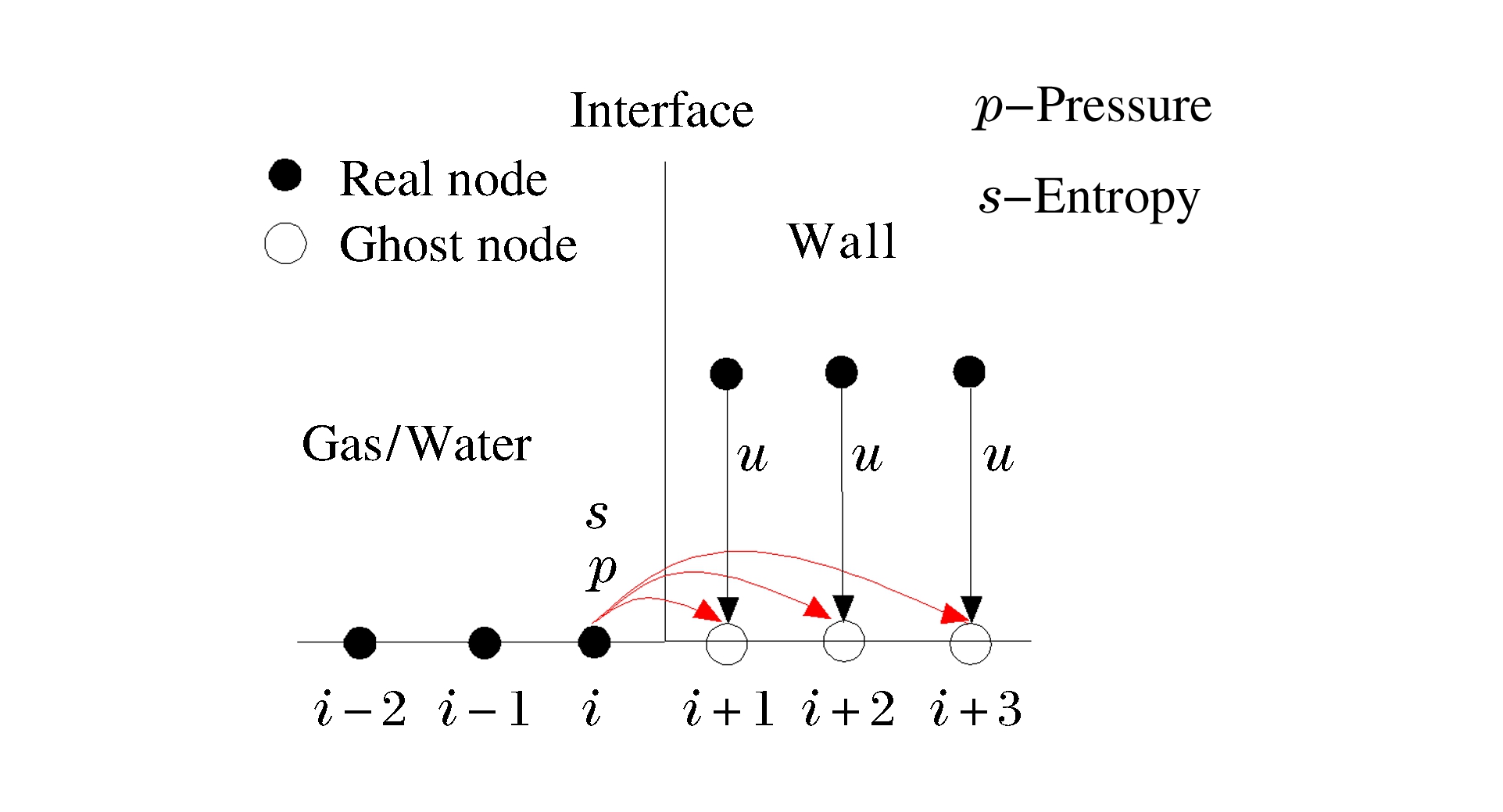
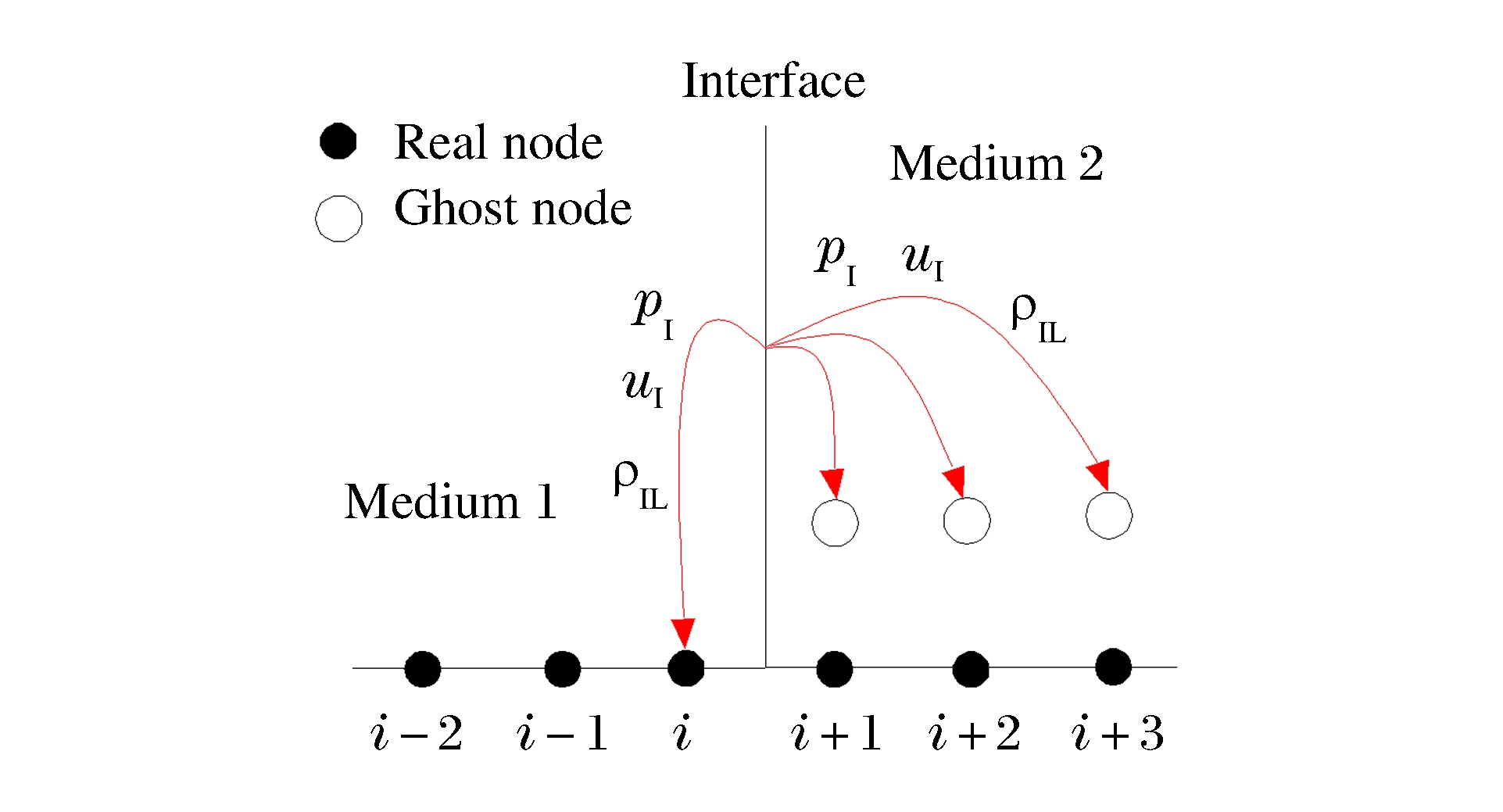
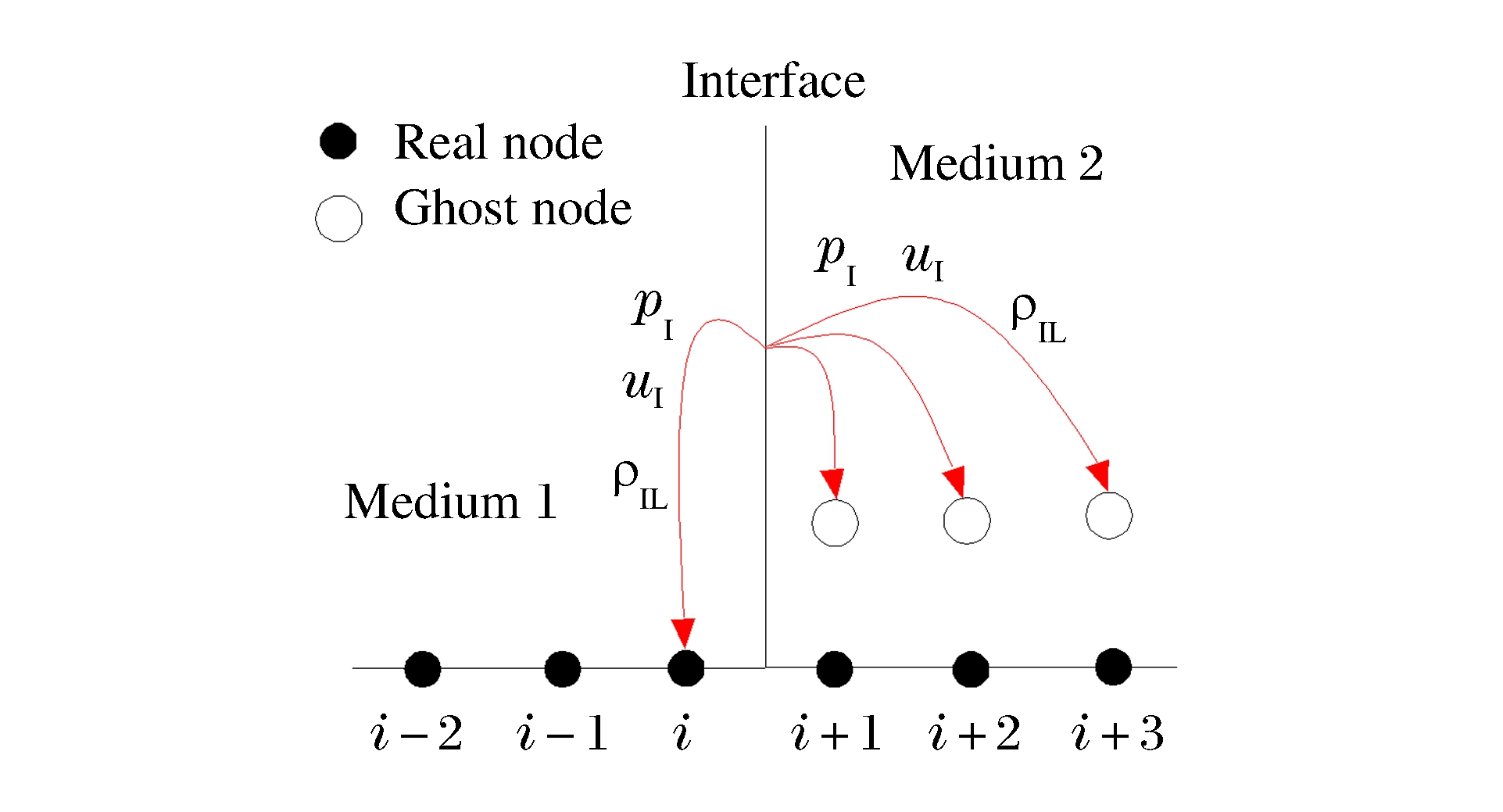
对于气-水界面的处理, 用RGFM法则。如图 1所示, 先用ARPS(Approximate Riemann Problem Solver)[15]求解界面参数, 包括界面压力pI、界面速度uI、界面左侧流体密度ρIL和界面右侧流体密度ρIR(下标“I”表示物质界面), 然后再对界面附近的网格节点用RGFM法则进行赋值。一维情况下, 将界面参数pI、uI、ρIL赋给真实节点i和虚拟节点(i+1)、(i+2)、(i+3)。二维情况下, 先将界面两侧法向偏转角度最小的两个节点代入一维模型求解界面参数, 然后对真实流体的节点进行赋值, 再外推到虚拟流体一侧的节点, 外推公式为
图 1 RGFM中气-水界面附近节点赋值示意图(一维模型)Figure 1. Updating the real and ghost nodes bordering the gas-liquid interface in RGFM (1D)∇φ⋅∇I=0 (5) 式中:I表示需要外推的变量, 具体可参考文献[16]。
2.5 NGFM
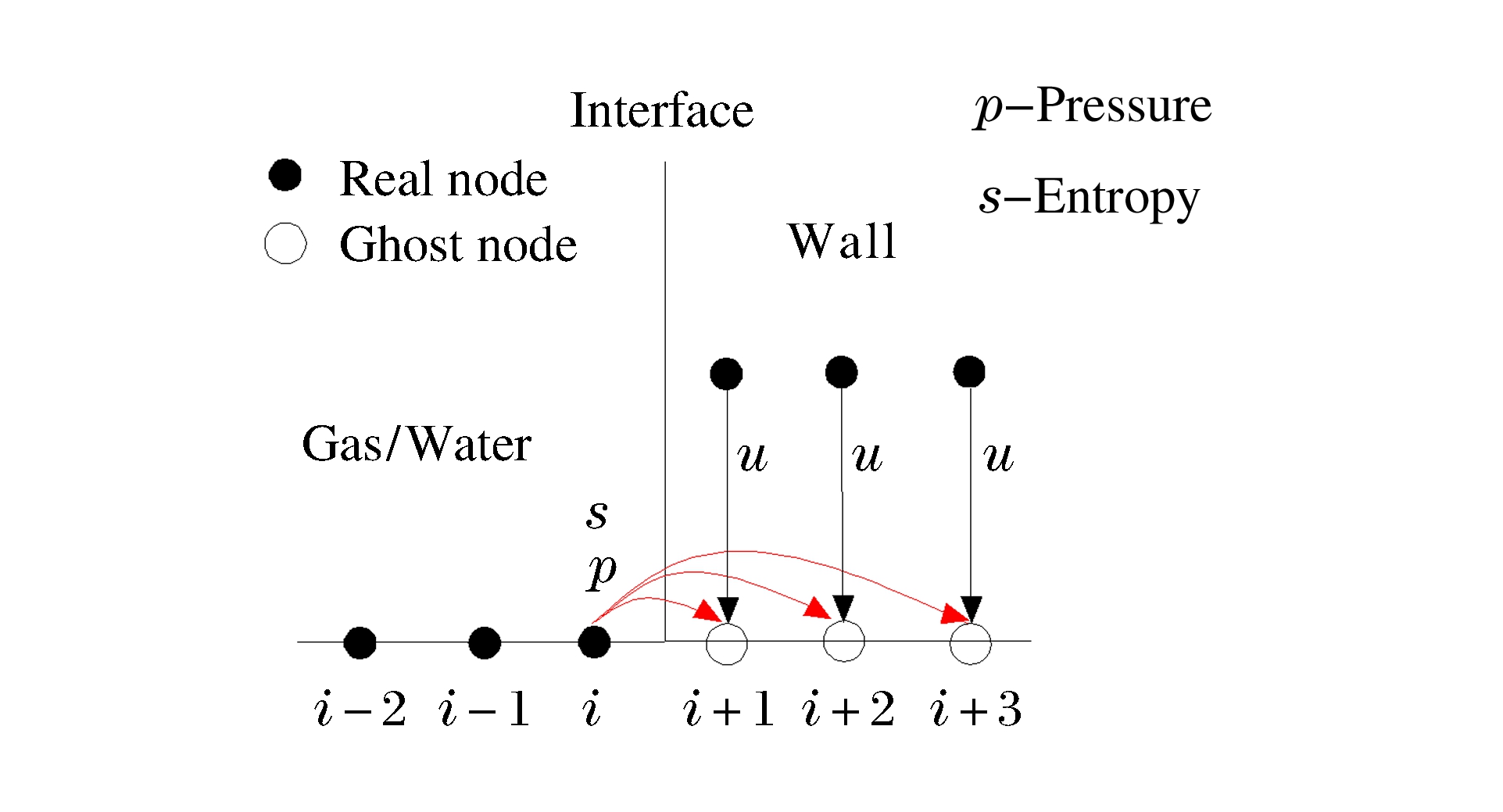
用NGFM处理固壁边界条件。如图 2所示, 将固壁边界拓展为一种物质, 将流体压力和熵越过边界外推到虚拟节点。虚拟节点的速度直接用当地速度, 本研究中认为固壁不移动, 即当地速度为零。对于二维数值计算, 固壁速度u、v均设为零, 并直接赋给虚拟节点。
图 2 NGFM中流-固界面附近节点赋值示意图(一维模型)Figure 2. Updating the real and ghost nodes next to the liquid-solid interface in NGFM (1D)2.6 状态方程
对于欧拉方程, 空间方向采用五阶WENO (Weighted Essentially Non-Oscillatory)格式[17]求解, 时间方向采用二阶Runge-Kutta (R-K)法求解; 对于Level Set方程, 空间方向采用HJ-WENO (Hamilton-Jacobi WENO)格式[18]求解, 时间方向采用三阶R-K法[19]求解。
3. 算例
3.1 一维考核算例
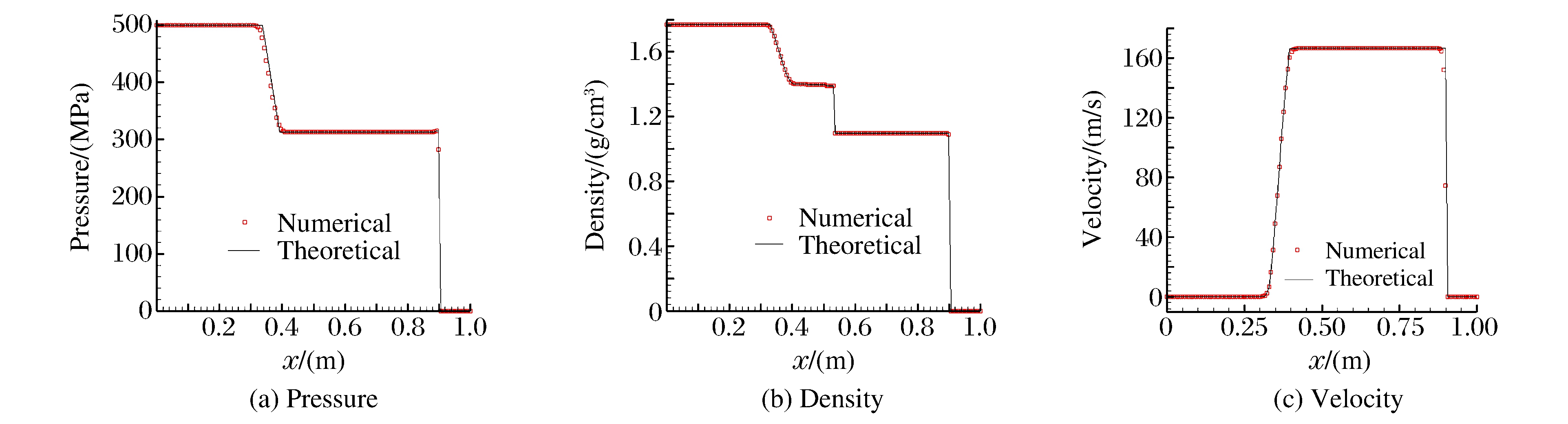
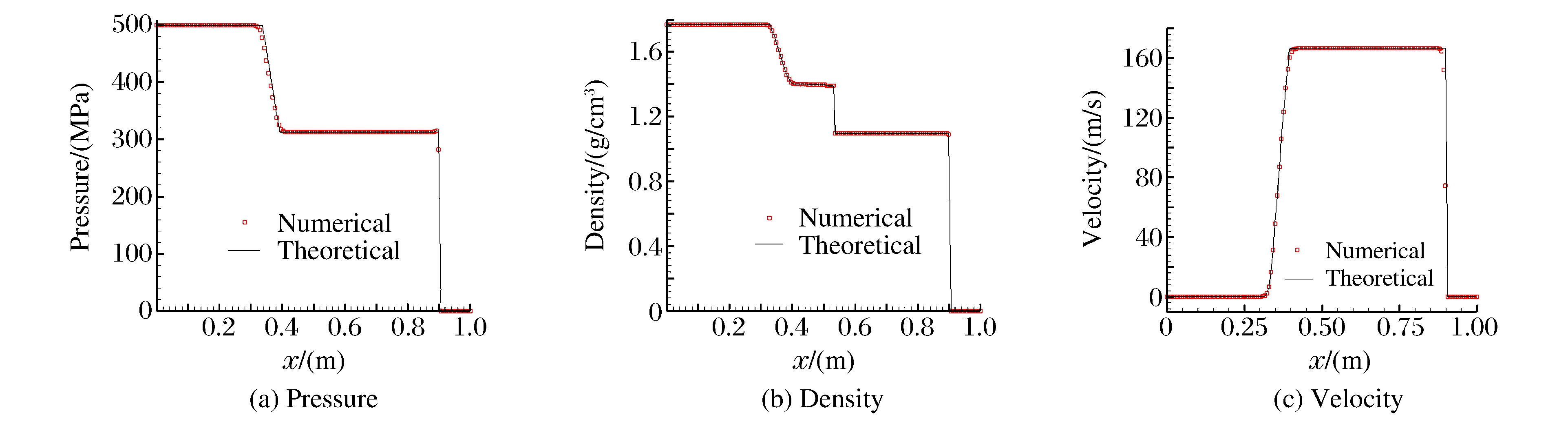
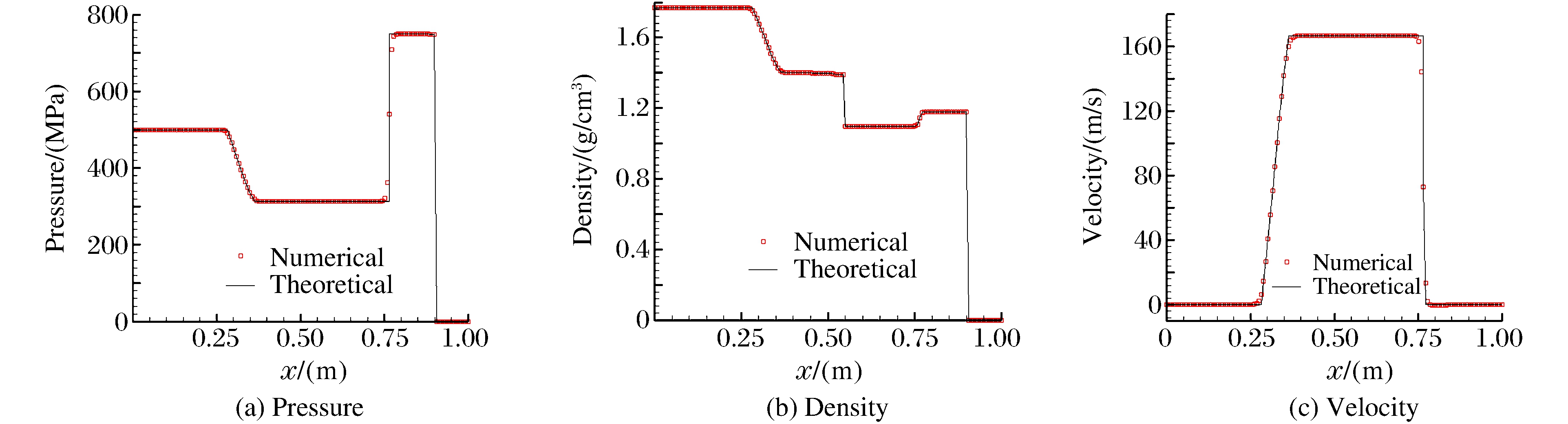
计算区域取x∈[0, 1], 初始时刻气-水界面位于x=0.5, 固壁边界位于x=0.9。区域[0, 0.5]为高压气体, 初始参数γg=2.0, pg=500 MPa, ρg=1.77 g/cm3; [0.5, 0.9]为水, 初始参数pL=0.1 MPa, ρL=1.0 g/cm3; [0.9, 1.0]为固壁。如图 3所示, t=0.210 ms时, 激波到达固壁边界, 并开始反射。图 4描述了在t=0.270 ms时激波从固壁反射的情况。图 3和图 4表明, 使用NGFM处理固壁边界条件的数值计算结果和理论计算结果吻合得很好。
图 3 t=0.210 ms时，用NGFM处理固壁边界的数值解和理论解的比较Figure 3. Comparison of results using NGFM to treat the wall boundary with the theoretical results at t=0.210 ms
图 4 t=0.270 ms时，用NGFM处理固壁边界的数值解和理论解的比较Figure 4. Comparison of the results using NGFM to treat the wall boundary with the theoretical results at t=0.270 ms3.2 二维复杂计算域的水下高压气泡膨胀
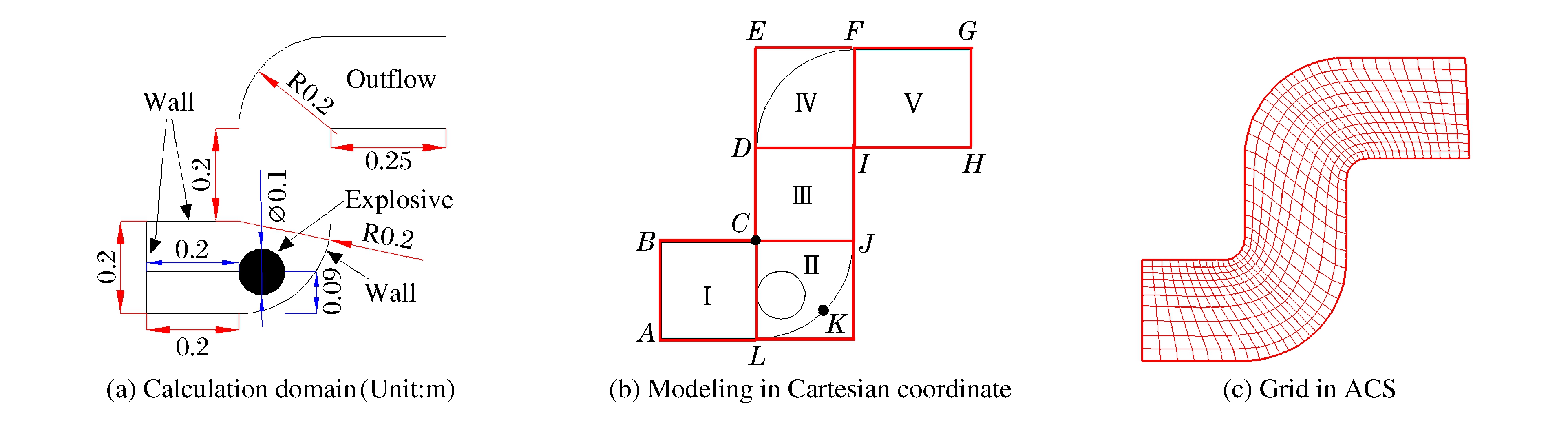
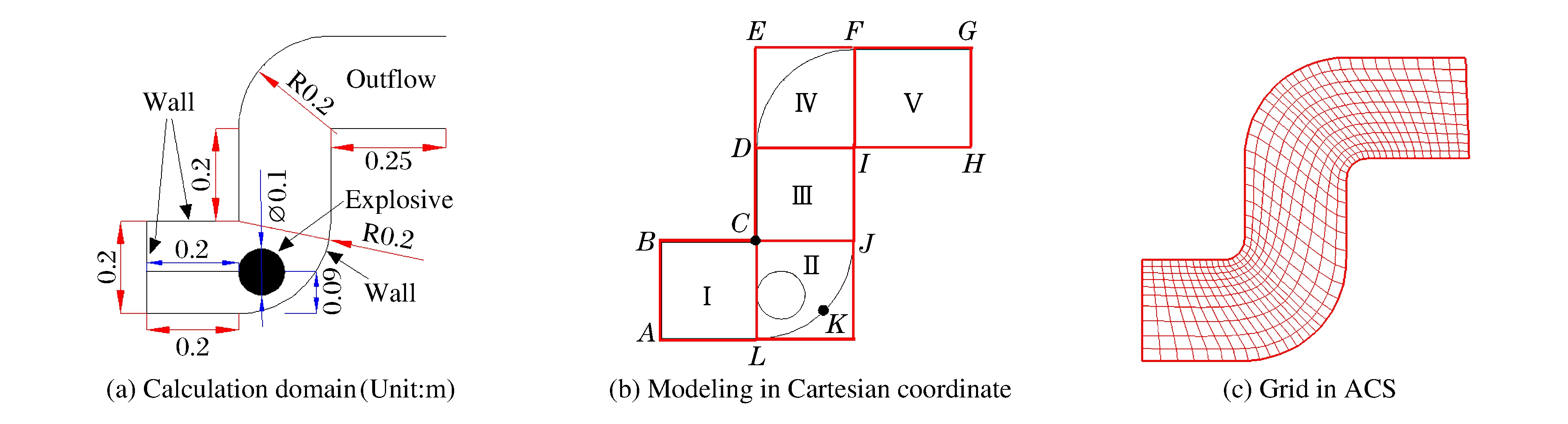
如图 5(a)所示, 高压气体的直径为0.1 m。如图 5(b)所示, 在直角坐标系下, 将计算区域划分成5块以减少计算网格。也可以不分块, 但是需要用一个较大的方形计算区域将整个复杂计算域包起来。分块后, 在每一块区域内划分笛卡尔网格进行计算, 取Δx=Δy=5 mm。图 5(b)中, C点是弯头的拐角, K点是弧形壁面
的中点, 计算中考察C点和K点的动态响应。在直角坐标系下, 固壁的Level Set界面上没有网格节点, 所以选取离C点和K点最近的网格节点输出p-t曲线。高压气体初始参数设为γg=2.0, pg=139 MPa, ρg=1.0 g/cm3; 水的初始参数为pl=0.1 MPa, ρl=1.0 g/cm3。本研究还提供任意坐标系(Arbitrary Coordinate System, ACS)下的结果作为对比。如图 5(c)所示, 在任意坐标系下, 对计算域划分合适的网格(实际网格数量为图中显示的16倍)。同时, 为了避免网格导数不连续, 对C点和I点两个拐角做近似光滑处理。任意坐标系下的Euler方程采用二阶TVD(Total Variation Diminishing)和二阶R-K离散, Level Set方程也需要进行坐标变换, 具体可参考文献[20]。
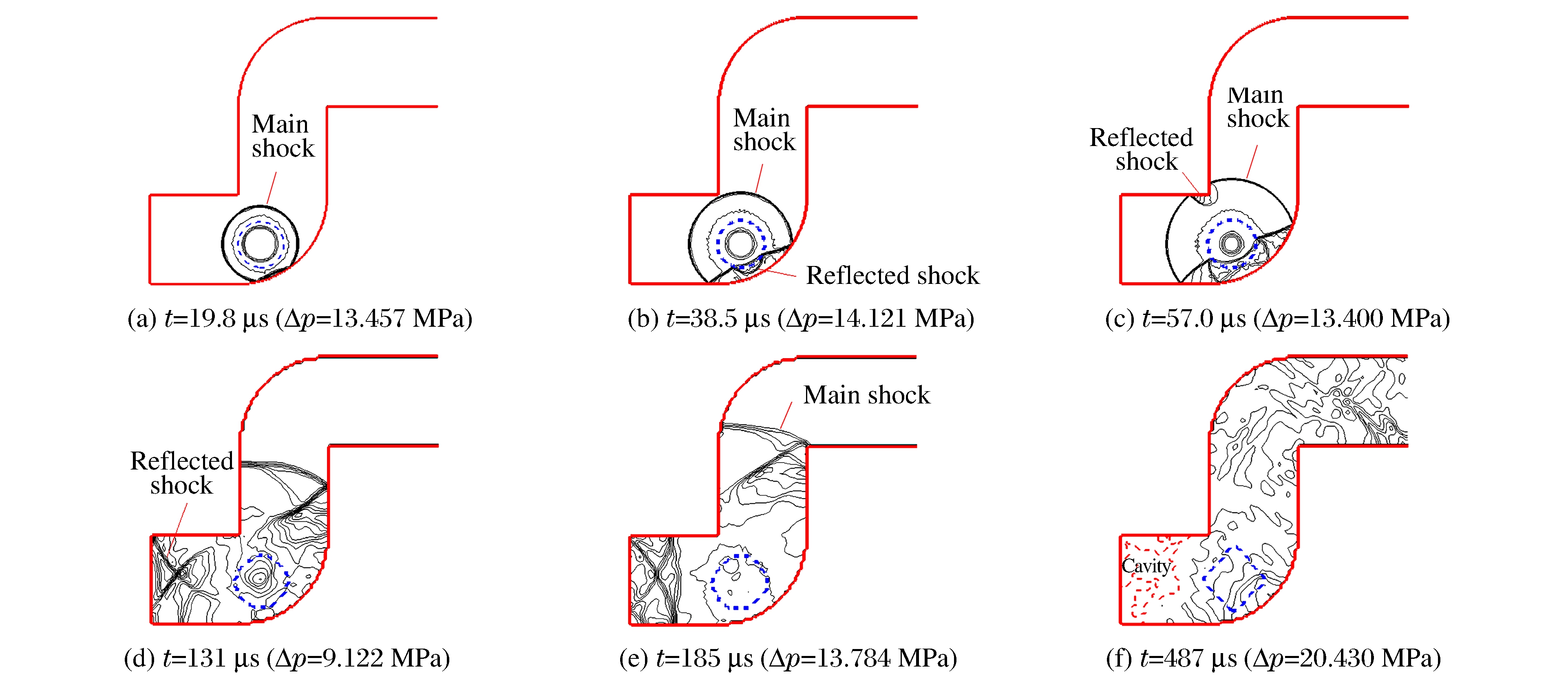
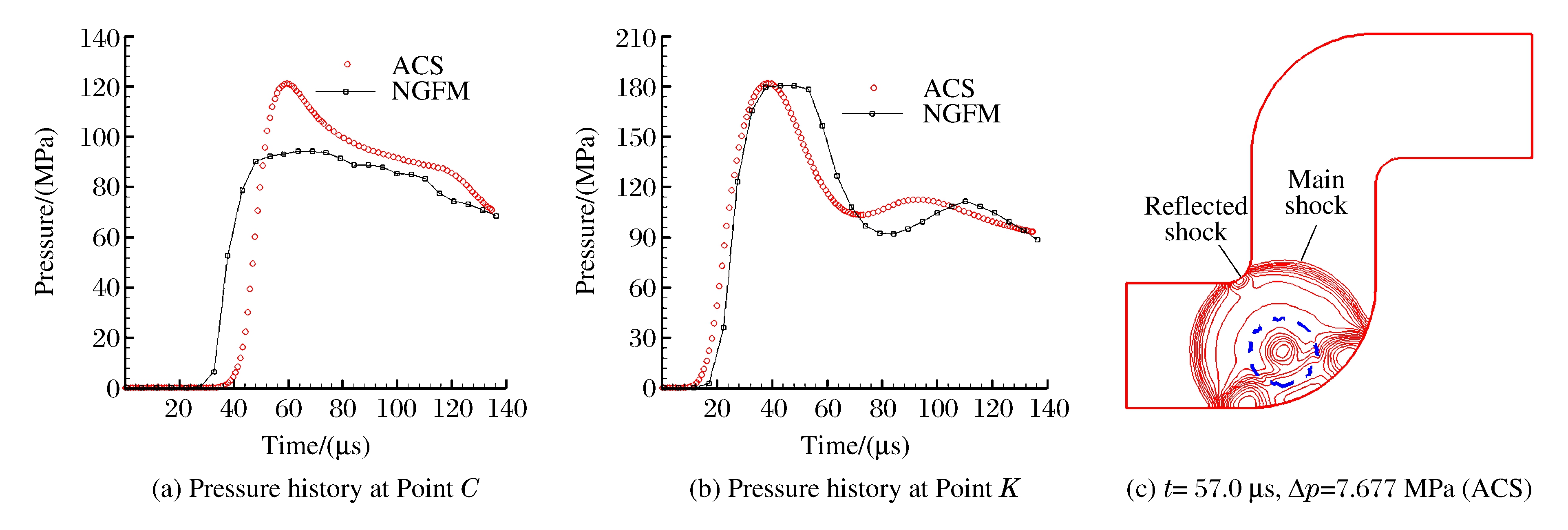
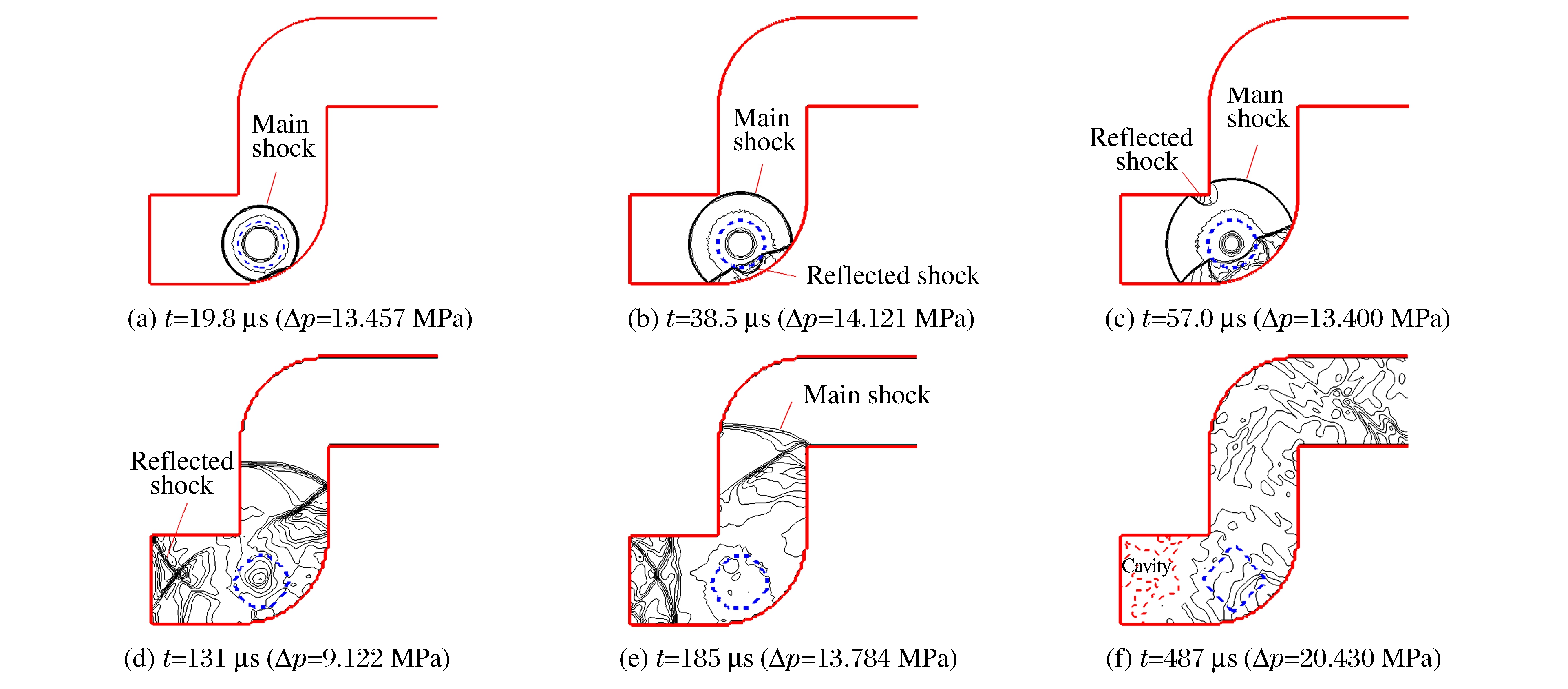
图 6(a)中, 大约t=19.8 μs时, 激波到达K点, 并产生反射波。图 6(b)中, t=38.5 μs时, 从
段反射的激波撞击高压气泡, 抑制高压气泡的膨胀, 并再次反射, 产生稀疏波; 该稀疏波将再次从
段反射, 并再次抑制高压气泡的膨胀。图 6(c)中, t=57.0 μs时, 激波到达计算域拐点C处, 并发生反射; 该反射波也将打向高压气泡, 从另一侧抑制高压气泡的膨胀。图 6(d)中, t=131 μs时, 来自固壁AB和固壁BC的反射波发生叠加。图 6(e)显示, 激波传播到计算域上部拐角I点处用时约185 μs。从图 6(f)中可以看出, 强激波从固壁的反射造成固壁附近大范围的空化。图 6(a)~图 6(f)也描述了高压气泡体积的变化过程, 在周围反射激波的作用下, 高压气泡的膨胀受到了强烈抑制。
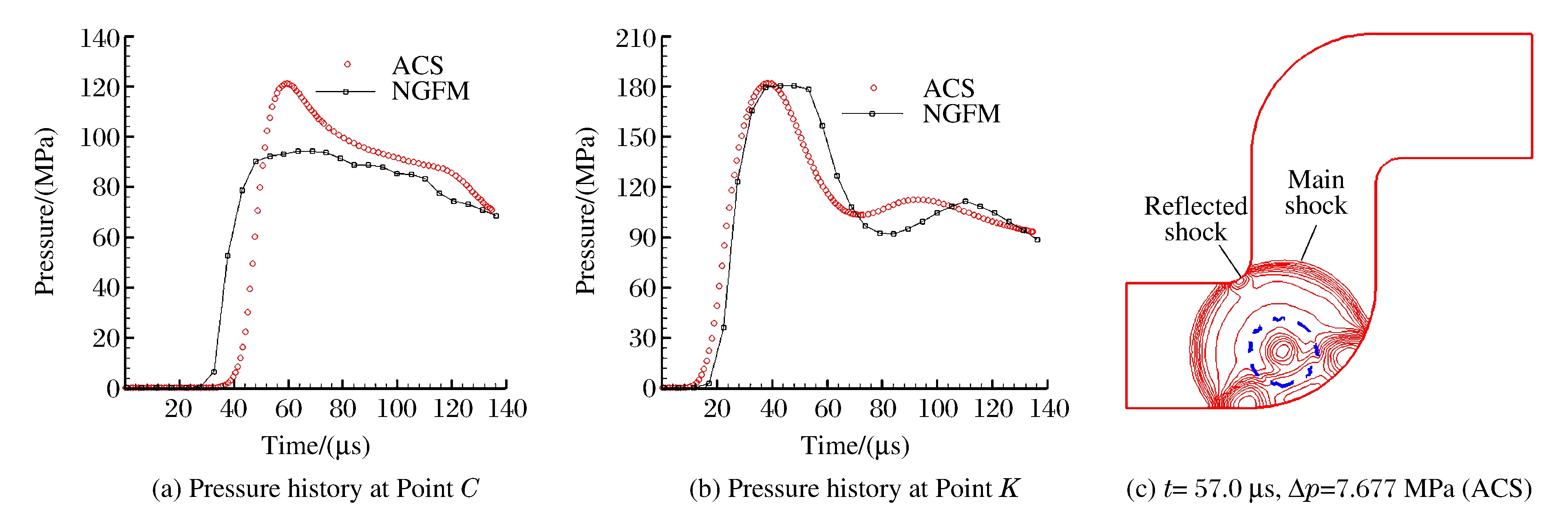
图 6 激波传播和高压气泡变化过程(蓝色虚线表示高压气泡，红色虚线表示空化区域；Δp为相邻压力等值线间的压差)Figure 6. Shock wave propagation and change process of high pressure bubble (Blue dashed line indicates high pressure bubble, red dashed line indicates cavitation region; Δp indicates the pressure difference between adjacent isolines)如图 7(a)所示, 由于对任意坐标系下的计算域拐角处做了近似光滑处理, 它与高压气泡的距离被人为地扩大, 所以任意坐标系下C点处, 压力开始上升的时间应比理论时间晚; 同时, 激波的能量在拐角处积累的时间也相应地延长, 故压力峰值也应高于真实值。如图 7(b)所示, 在直角坐标系下, 选择离K点最近的网格节点输出p-t曲线, 由于该节点在计算域内部, 所以压力上升时间迟于任意坐标下的压力上升时间, 下降时间也迟, 压力峰值略小, 但二者压力变化趋势是一致的。比较图 6(c)和图 7(c), NGFM的流场结果和任意坐标系的流场结果吻合。因为网格导数的引入, 任意坐标系的结果较直角坐标系下NGFM的结果略粗糙。以上对比和分析表明, 用NGFM计算的结果同理论情况一致。
图 7 NGFM计算结果和任意坐标系下计算结果的比较Figure 7. Comparison of the results using NGFM to treat wall boundary with the results in arbitrary coordinate system4. 结论
将复杂计算域的固壁边界拓展成一种物质, 用NGFM对拓展区域的虚拟网格节点赋值, 以二维90°弯头为例, 给出了水下高压气泡的膨胀过程、流场压力等值线以及两个指定点的p-t曲线。通过与任意坐标系下的计算结果进行对比, 验证了NGFM在直角坐标系下处理复杂形状固壁边界的可行性。计算结果表明, 高压气泡在固壁反射激波的作用下, 膨胀会受到强烈抑制; 强激波在固壁的反射会导致固壁附近出现大范围的空化流动。
致谢: 感谢中国科学技术大学多相流和化学反应流实验室的李应林博士, 帮助作者绘制3.2节中任意坐标系下的网格。 -
图 1 RGFM中气-水界面附近节点赋值示意图(一维模型)
Figure 1. Updating the real and ghost nodes bordering the gas-liquid interface in RGFM (1D)
图 2 NGFM中流-固界面附近节点赋值示意图(一维模型)
Figure 2. Updating the real and ghost nodes next to the liquid-solid interface in NGFM (1D)
图 3 t=0.210 ms时，用NGFM处理固壁边界的数值解和理论解的比较
Figure 3. Comparison of results using NGFM to treat the wall boundary with the theoretical results at t=0.210 ms
图 4 t=0.270 ms时，用NGFM处理固壁边界的数值解和理论解的比较
Figure 4. Comparison of the results using NGFM to treat the wall boundary with the theoretical results at t=0.270 ms
图 6 激波传播和高压气泡变化过程(蓝色虚线表示高压气泡，红色虚线表示空化区域；Δp为相邻压力等值线间的压差)
Figure 6. Shock wave propagation and change process of high pressure bubble (Blue dashed line indicates high pressure bubble, red dashed line indicates cavitation region; Δp indicates the pressure difference between adjacent isolines)
-
[1] Blake J R, Gibson D C. Growth and collapse of a vapour cavity near a free surface[J]. J Fluid Mech, 1981, 111: 123-140. doi: 10.1017/S0022112081002322 [2] Pearson A, Cox E, Blake J R, et al. Bubble interactions near a free surface[J]. Eng Anal Bound Elem, 2004, 28(4): 295-313. doi: 10.1016/S0955-7997(03)00079-1 [3] Liu M B, Liu C R, Lam K Y. A one dimensional mesh free particle formulation for simulating shock waves[J]. Shock Waves, 2003, 13: 201-211. doi: 10.1007/s00193-003-0207-0 [4] Liu M B, Liu C R, Zong Z, et al. Numerical simulation of underwater explosion by SPH[J]. Advan Comput Eng Sci, 2000: 1475-1480. [5] Liu M B, Liu C R, Zong Z, et al. Computer simulation of the high explosive explosion using smoothed particle hydrodynamics methodology[J]. Comput Fluids, 2003, 32(3): 305-322. http://www.sciencedirect.com/science/article/pii/S0045793001001050 [6] Vernon T A. Whipping response of ship hulls from underwater explosion bubble loading, AD-A178096[R]. Nova Scotia: Defence Research Establishment Atlantic Dartmouth, 1986. [7] Zong Z. A hydroplastic analysis of a free-free beam floating on water subjected to an underwater bubble[J]. J Fluid Struct, 2005, 20(3): 359-372. doi: 10.1016/j.jfluidstructs.2004.08.003 [8] Zhang A M, Yang W S, Huang C, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination[J]. Comput Fluids, 2013, 71: 169-178. doi: 10.1016/j.compfluid.2012.10.012 [9] Fedkiw R P. Coupling an Eulerian fluid calculation to a Lagrangian solid calculation with the ghost fluid method[J]. J Comput Phys, 2002, 175(1): 200-224. http://doi.ieeecomputersociety.org/resolve?ref_id=doi:10.1006/jcph.2001.6935&rfr_id=trans/tg/2009/03/ttg2009030493.htm [10] Wang C W, Liu T G, Khoo B C. A real ghost fluid method for the simulation of multimedium compressible flow[J]. J Sci Comput, 2005, 28(1): 278-302. http://dl.acm.org/citation.cfm?id=1122832 [11] Wardlaw A B Jr. Underwater explosion test cases, IHTR-2069[R]. Maryland: Naval Surface Warfare Center Indian Head Division, 1998. [12] Liu T G, Khoo B C, Xie W F. Isentropic one-fluid modelling of unsteady cavitating flow[J]. J Comput Phys, 2004, 201(1): 80-108. http://www.ams.org/mathscinet-getitem?mr=2098854 [13] Osher S, Sethian J A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. J Comput Phys, 1988, 79(1): 12-49. http://www.ams.org/mathscinet-getitem?mr=965860 [14] Sussman M, Smereka P, Osher S. A level set approach for computing solutions to incompressible two-phase flow[J]. J Comput Phys, 1994, 114(1): 146-159. [15] Liu T G, Khoo B C, Yeo K S. Ghost fluid method for strong shock impacting on material interface[J]. J Comput Phys, 2003, 190(2): 651-681. http://www.sciencedirect.com/science/article/pii/S0021999103003012 [16] Adalsteinsson D, Sethian J A. The fast construction of extension velocities in level set methods[J]. J Comput Phys, 1999, 148(1): 2-22. http://www.sciencedirect.com/science/article/pii/s0021999198960909 [17] Shu C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws, ICASE Report[R]. Rhode Island: Brown University, 1997. [18] Jiang G S, Peng D. Weighted ENO schemes for Hamilton Jacobi equations[J]. SIAM J Sci Comput, 2000, 21(6): 2126-2143. doi: 10.1137/S106482759732455X [19] Shu C W, Osher S. Efficient implementation of essentially non-oscillatory shock capturing schemes[J]. J Comput Phys, 1988, 77(2): 439-471. [20] 曹乐.利用Level set方法捕捉气、水界面的三维数值研究[D].合肥: 中国科学技术大学, 2009: 20-21.Cao L. Three-dimensional computations on capturing of gas-water interface by level set method[D]. Hefei: University of Science and Technology of China, 2009: 20-21. (in Chinese) -
下载:
下载:
点击查看大图
计量
- 文章访问数: 6812
- HTML全文浏览量: 2345
- PDF下载量: 255
