非饱和黏土平板撞击实验及状态方程的研究

丁育青; 汤文辉; 张若棋; 冉宪文; 张明建

doi:10.11858/gywlxb.2014.06.002

非饱和黏土平板撞击实验及状态方程的研究

doi: 10.11858/gywlxb.2014.06.002

丁育青^{1, 2,},
汤文辉^1,*, ,,
张若棋¹,
冉宪文¹,
张明建³

1.
国防科学技术大学理学院工程物理研究所，湖南长沙 410073
2.
第二炮兵装备研究院第二研究所, 北京 100085
3.
西南交通大学高压物理实验室，四川成都 610031

基金项目: 国家安全重大基础研究项目; 国家自然科学基金(11002162)

详细信息

作者简介:
丁育青(1985—), 男，博士，主要从事材料动态力学性能研究.E-mail:yqding_nudt@163.com

通讯作者:
汤文辉(1964—), 男，博士，教授，主要从事冲击波物理研究.E-mail:wenhuitang@163.com

中图分类号: O521.2; TU411.5
计量
- 文章访问数: 6835
- HTML全文浏览量: 2259
- PDF下载量: 193
出版历程
- 收稿日期: 2012-12-17
- 修回日期: 2013-03-06

Equation of State for Unsaturated Clay by Plate Impact Experiments

1.
Institute of Engineering Physics, College of Science, National University of Defense Technology, Changsha 410073, China
2.
The Second Institute of the Second Artillery Equiqment Academe, Beijing 100085
3.
Laboratory of High-Pressure Physics, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要: 利用口径为24 mm的二级轻气炮实验装置，结合磁测速和光纤探针动态测试技术，分别对含水率为0、8%和15%的3种非饱和黏土试样进行了平板撞击实验，试样的压力峰值区间为1.29~32.54 GPa。实验结果表明，含水率对非饱和黏土的冲击压缩特性影响明显。当非饱和黏土受到冲击压缩时，孔隙被进一步压实，滞留在黏土孔隙中的水和空气来不及排出，从而与黏土中的固体颗粒一起，共同支配非饱和黏土的冲击压缩特性；而由于水的相对不可压缩性，导致黏土的可压缩性随着含水率的升高而下降。提出一种修正的三相混合物状态方程，对3种含水率试样的压力-密度曲线进行了拟合，结果表明，该状态方程能够较好地描述不同含水率非饱和黏土的压力-密度关系。
- 非饱和黏土 /
- 含水率 /
- 二级轻气炮 /
- 平板撞击实验 /
- 状态方程
Abstract: Using a 24 mm bore two-stage light gas gun, plate impact experiments were performed on unsaturated clay at 3 moisture contents-0, 8% and 15%-to obtain its Hugoniot data.The shock wave motions in the samples were detected by fiber-optic pins, and the pressure in the sample ranged from 1.29 to 32.54 GPa.The experiment results indicate that the moisture content has a significant effect on the shock compression properties of unsaturated clay.While compressed, the gas and water in pores cannot escape promptly due to the transient loading time, thus they dominate the shock compression properties of unsaturated clay together with the solid grains.Since water is much stiffer than gas, the compressibility of unsaturated clay decreases as the moisture content increases.Besides, a modified three-phase equation of state is introduced to describe the pressure-density relationship of the unsaturated clay, which shows good agreement with the experimental data.
- unsaturated clay /
- moisture content /
- two-stage light gas gun /
- plate impact /
- equation of state

HTML全文

1. 引言

土是目前各类民用和国防工程中最常用的基层材料, 当上层构筑物承受爆炸、冲击等强动载荷时, 土的冲击特性与整体结构的抗冲击性能有密切关系; 因此, 研究强动载荷下土的冲击特性具有重要的实际意义。

一般认为, 土是由构成土骨架的固体颗粒、孔隙中的水和气体组成的三相介质^[1]。Tsembelis等人^[2]、Resnyansky等人^[3]、Chapman等人^[4-6]、Brown等人^[7]、Bragov等人^[8]及Arlery等人^[9]利用一级轻气炮实验装备, 应用锰铜压阻计或VISAR等测试技术, 分别对不同粒径分布、初始密度以及含水率的砂土试样进行了平板撞击实验, 试样的压力峰值均在10 GPa以下。结果表明, 粒径分布、初始密度及含水率等因素对砂土的冲击性能影响明显。目前, 针对黏土在高压下的平板撞击实验研究仍未见报道。在土的状态方程研究方面, Resnyansky等人^[3]提出了一种两相混合物状态方程, 方程基于混合物状态方程的思想, 当用于描述干砂土时, 它由气体和固体颗粒的状态方程组成; 当用于描述含水砂土时, 则由水和固体颗粒的状态方程组成。该模型忽略了孔隙气体对非饱和土冲击压缩性能的影响^[10]。Wang等人^[11-12]根据Kaudaur的设想, 将固体颗粒、水和气体按照各自比例混合在一起, 使用三相混合物状态方程开展相关动态过程的数值模拟^[1], 结果表明, 该模型能够较好地描述土在爆炸载荷下的动态行为。

本研究利用二级轻气炮实验装置, 对3种含水率的非饱和黏土试样进行平板撞击实验研究, 分析含水率对非饱和黏土冲击特性的影响规律, 研究并改进土的三相混合物状态方程。

2. 实验

2.1 实验准备

土具有很强的地域特征, 不同类别土的冲击特性差异很大。实验所用黏土取自洛阳地区, 采用密度计法进行土样的颗粒分析实验, 测得固体颗粒密度ρ_s=2.74 g/cm³, 颗粒分析结果如表 1所示。试样干密度ρ_d=1.70 g/cm³, 孔隙比e=0.61, 试样尺寸为∅16 mm×3 mm, 含水率w分别为0、8%和15%, 对应的饱和度S_r分别为0、35.9%和67.4%。

表 1 黏土试样颗粒分析结果

Table 1. Particle size distribution in the clay sample

Particle dimension/ (mm)	Mass proportion/ (%)
<0.005	28.6
0.005-0.075	71.4
>0.075	0

下载: 导出CSV

| 显示表格

2.2 实验方法

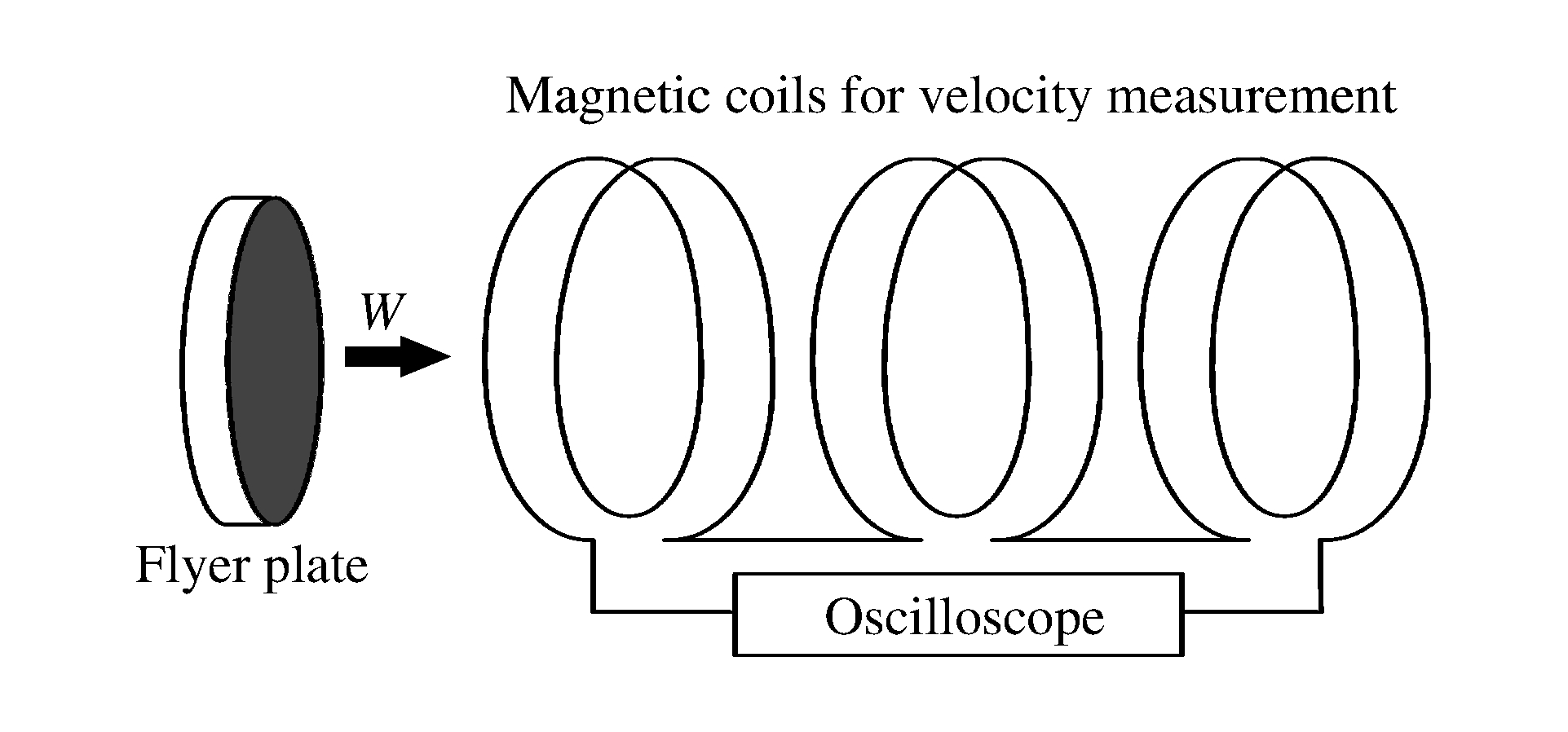
实验在西南交通大学高压物理实验室∅24 mm二级轻气炮上完成。飞片尺寸为∅24 mm×3 mm, 材料参数如表 2所示, 其中, λ为Hugoniot参数。利用磁测速系统测量飞片速度, 在飞片飞行途中的几个固定位置处放置磁环, 如图 1所示。当金属飞片在磁环产生的非均匀强磁场中运动时, 会在表面感应产生涡旋电流, 并在线圈中产生感应电动势。利用示波器记录这种感生电动势随时间的变化曲线, 在已知线圈间距的条件下, 再利用示波器读取间隔时间, 便可计算得到飞片速度W。

表 2 飞片材料参数

Table 2. Parameters of flyer plate materials

Material	Density/ (g/cm³)	Sound speed/ (km/s)	λ
Al alloy	2.785	5.328	1.338
Cu	8.93	3.940	1.489
Ta	16.656	3.437	1.19

下载: 导出CSV

| 显示表格

图 1 磁测速原理示意图

Figure 1. Schematic of magnetic measurement of velocity

下载: 全尺寸图片幻灯片

实验中采用光探针技术^[14]测量飞片和冲击波到达试样的时刻。试样碰撞面的外缘均匀布置4根光探针(编号A~D), 用于测量飞片撞击试样的时刻, 对角线上的2根光探针构成一组测量通道, 共两组测量通道, 对角布置的光探针还可修正碰撞过程中飞片倾斜的影响。同时, 在试样后界面中心位置布置一根光探针(编号E), 用于测量冲击波到达时刻。试样装配及测试原理如图 2所示。冲击波作用于光纤使其发光, 由此产生的光脉冲信号经光纤传输到光电探测器, 转换为电信号, 再由示波器记录, 通过判读可以确定飞片或冲击波到达光纤探针的时刻。

图 2 平板撞击实验示意图

Figure 2. Schematic of plate impact configuration before impact

下载: 全尺寸图片幻灯片

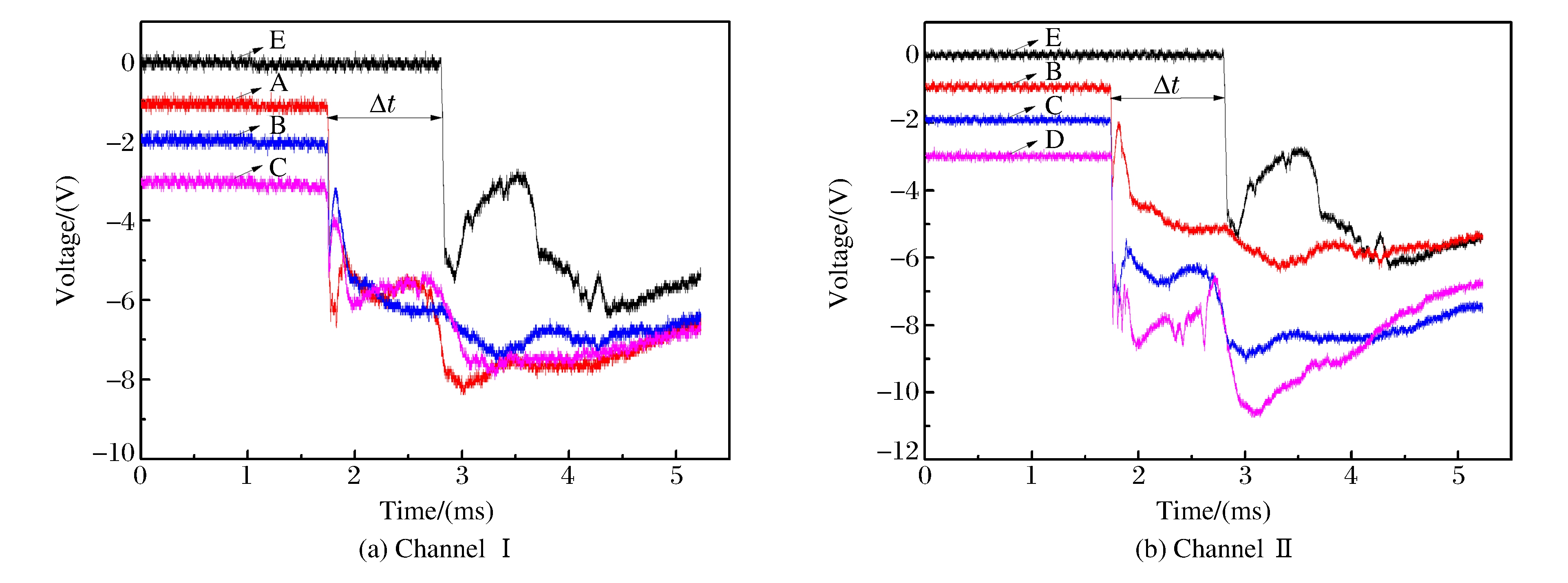
实验过程中, 两组测量通道测得的典型信号波形如图 3所示。图 3(a)中的信号分别由编号为E、A、B和C的4个光探针测得, 图 3(b)中的信号则分别由编号为E、B、C和D的4个光探针测得, 其中, 编号为E、B和C的3个探针的信号为重复测量。由图 3可以看出, A、B、C、D这4个光探针信号的起跳时刻基本吻合, 说明飞片撞靶时的平面性较好, 偏转角度较小。信号的第一个拐点指示了飞片或冲击波到达每根探针的时刻, 故试样中的冲击波速度D可由下式求出

图 3 实验测得的典型探针信号

Figure 3. Signal of fiber-optic pins measured in experiments

下载: 全尺寸图片幻灯片

$D=\Delta h / \Delta t$

(1)

式中:Δh为试样厚度, Δt为冲击波在试样中传播的时间。

对于大多数材料, 冲击波速度D与波后质点速度u呈线性关系, 即

$D=c_{0}+\lambda u$

(2)

式中:c₀为材料声速, λ为Hugoniot参数。

根据冲击阻抗匹配的压力平衡方程和界面连续方程

$\rho_{\mathrm{f}}\left[c_{\mathrm{f}}+\lambda_{\mathrm{f}}\left(W-u_{\mathrm{f}}\right)\right]\left(W-u_{\mathrm{f}}\right)=\rho_{\mathrm{s}} D u_{\mathrm{s}}$

(3)

$u_{\mathrm{f}}=u_{\mathrm{s}}$

(4)

可得试样的质点速度

$u_{\mathrm{s}}=\frac{\left(\rho_{\mathrm{f}} c_{\mathrm{f}}+2 \rho_{\mathrm{f}} \lambda_{\mathrm{f}} W+\rho_{\mathrm{s}} D\right)-\left[\left(\rho_{\mathrm{f}} c_{\mathrm{f}}+2 \rho_{\mathrm{f}} \lambda_{\mathrm{f}} W+\rho_{\mathrm{s}} D\right)^{2}-4 \rho_{\mathrm{f}} \lambda_{\mathrm{f}}\left(\rho_{\mathrm{f}} c_{\mathrm{f}} W+\rho_{\mathrm{f}} \lambda_{\mathrm{f}} W^{2}\right)\right]^{\frac{1}{2}}}{2 \rho_{\mathrm{f}} \lambda_{\mathrm{f}}}$

(5)

式中:W为撞击前飞片的运动速度, ρ_f、c_f、u_f、λ_f分别为飞片的密度、声速、质点速度和Hugoniot参数, ρ_s、u_s分别为试样的密度和质点速度。

2.3 实验结果

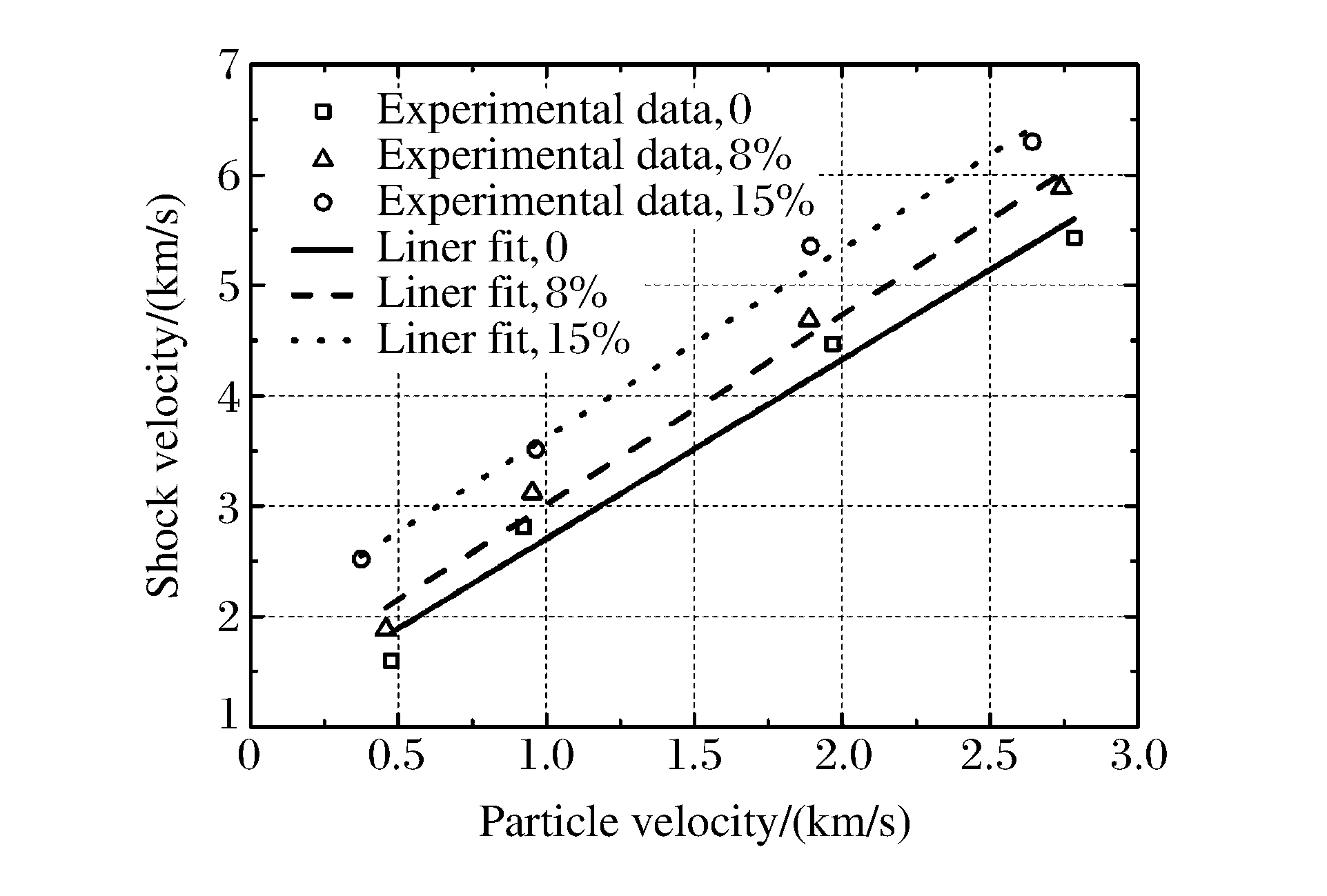
按照3种含水率的试样, 将实验分为3组, 每组4发实验, 各发实验情况如表 3所示。对黏土试样的D-u实验结果按照(2)式进行线性拟合, 结果如图 4所示。根据(2)式计算得到, 含水率为0的黏土试样c₀=1.078 km/s、λ=1.624, 含水率为8%的黏土试样c₀=1.913 km/s、λ=1.707, 含水率为15%的黏土试样c₀=1.289 km/s、λ=1.722。由此, 可得3种含水率试样的Hugoniot曲线, 如图 5所示。由图 5可以看出, 随着含水率的上升, 试样的可压缩性下降, 这是由于在高应变率和高压加载条件下, 滞留在试样孔隙中的水和空气不能排出, 它们与固体颗粒一起, 共同支配非饱和黏土的冲击压缩特性。而由于水的相对不可压缩性, 导致黏土的可压缩性随着含水率的升高而下降。

表 3 平板撞击实验结果

Table 3. Results of plate impact experiments

Sample condition	Flyer material	Flyer velocity/ (km/s)	Shock arrival time/ (ns)	Sample thickness/ (mm)	Particle velocity/ (km/s)	Shock velocity/ (km/s)	Longitudinal stress/ (GPa)
Dry clay	Al	0.561	1 868	2.98	0.48	1.60	1.29
	Cu	1.042	1 054	2.96	0.92	2.81	4.40
	Cu	2.340	658	2.94	1.97	4.47	14.95
	Ta	3.180	556	3.02	2.79	5.43	25.71
Wet clay (Moisture content=8%)	Al	0.563	1 564	2.94	0.46	1.88	1.58
	Cu	1.101	956	2.98	0.95	3.12	5.46
	Cu	2.290	640	3.00	1.89	4.69	16.26
	Ta	3.190	500	2.94	2.74	5.88	29.60
Wet clay (Moisture content=15%)	Al	0.495	1 192	3.00	0.37	2.52	1.84
	Cu	1.142	848	2.98	0.97	3.51	6.63
	Cu	2.370	538	2.88	1.89	5.35	19.81
	Ta	3.130	478	3.01	2.64	6.30	32.54

下载: 导出CSV

| 显示表格

图 4 黏土试样的D-u关系

Figure 4. The relationship between D and u of clay specimen at different moisture contents

下载: 全尺寸图片幻灯片

图 5 黏土试样的p-ρ Hugoniot曲线

Figure 5. The p-ρ Hogoniot curves of clay specimen at different moisture contents

下载: 全尺寸图片幻灯片

3. 三相混合物状态方程

如前所述, 土可看作是由固体颗粒、孔隙中的水和气体组成的三相介质。压缩前, 初始状态土的体密度为ρ₀, 记作

$\rho_{0}=\frac{m}{V_{0}}=\frac{m_{\mathrm{g}}+m_{\mathrm{w}}+m_{\mathrm{s}}}{V_{\mathrm{g} 0}+V_{\mathrm{w} 0}+V_{\mathrm{s} 0}}$

(6)

式中:m为土的质量, V₀为初始体积; 下标g、w、s分别表示气体、水和固体颗粒, 下同。

引入各相的初始相对体积α_g0、α_w0、α_s0

$\left\{\begin{aligned} \alpha_{\mathrm{g} 0} &=V_{\mathrm{g} 0} / V_{0} \\ \alpha_{\mathrm{w} 0} &=V_{\mathrm{w} 0} / V_{0} \\ \alpha_{\mathrm{s} 0} &=V_{\mathrm{s} 0} / V_{0} \end{aligned}\right.$

(7)

显然有

$\alpha_{\mathrm{g} 0}+\alpha_{\mathrm{w} 0}+\alpha_{\mathrm{s} 0}=1$

(8)

当土承受较大压力时, 土的压缩性质取决于各组分介质的体积压缩量。当土中压力为p时, 土各组分介质的相对体积分别为

$\left\{\begin{aligned} \alpha_{\mathrm{g} p} &=V_{\mathrm{g} \rho} / V_{0} \\ \alpha_{\mathrm{w} p} &=V_{\mathrm{w} p} / V_{0} \\ \alpha_{\mathrm{s} p} &=V_{\mathrm{s} p} / V_{0} \end{aligned}\right.$

(9)

因而有

$\alpha_{\mathrm{g}p}+\alpha_{\mathrm{w} p}+\alpha_{\mathrm{s} p}=V / V_{0}$

(10)

式中:V=V_gp+V_wp+V_sp, 是压力为p时土的体积。由质量守恒原理可得, 当压力为p时, 土的密度为

$\rho=\frac{m}{V}=\frac{\rho_{0}}{\alpha_{\mathrm{g} p}+\alpha_{\mathrm{w} p}+\alpha_{\mathrm{s} p}}$

(11)

(11) 式中, α_gp和α_wp可用气体和水的状态方程求出。对气体, 采用空气的状态方程描述^[1]

$p=p_{0}\left(\frac{\rho_{\mathrm{g}}}{\rho_{\mathrm{g} 0}}\right)^{k_{\mathrm{g}}}$

(12)

式中:p₀=101.3 kPa, 为大气压力; ρ_g0=1.225 5 kg/m³, k_g=1.4。对于水, 可用如下状态方程^[1]

$p=p_{0}+\frac{\rho_{\mathrm{w} 0} c_{\mathrm{w} 0}^{2}}{k_{\mathrm{w}}}\left[\left(\frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{w} 0}}\right)^{k_{\mathrm{w}}}-1\right]$

(13)

式中:ρ_w0=1.0 g/cm³, c_w0=1 415 m/s, k_w=3。

对于固体颗粒, Henrych提出形式与水相似的状态方程^[1]

$p=p_{0}+\frac{\rho_{\mathrm{s} 0} c_{\mathrm{s} 0}^{2}}{k_{\mathrm{s}}}\left[\left(\frac{\rho_{\mathrm{s}}}{\rho_{\mathrm{s} 0}}\right)^{k_{\mathrm{s}}}-1\right]$

(14)

式中:ρ_s0=2.74 g/cm³, c_s0=4 500 m/s, k_s=3。

将(12)式、(13)式和(14)式代入(11)式, 可得土的三相混合物状态方程为

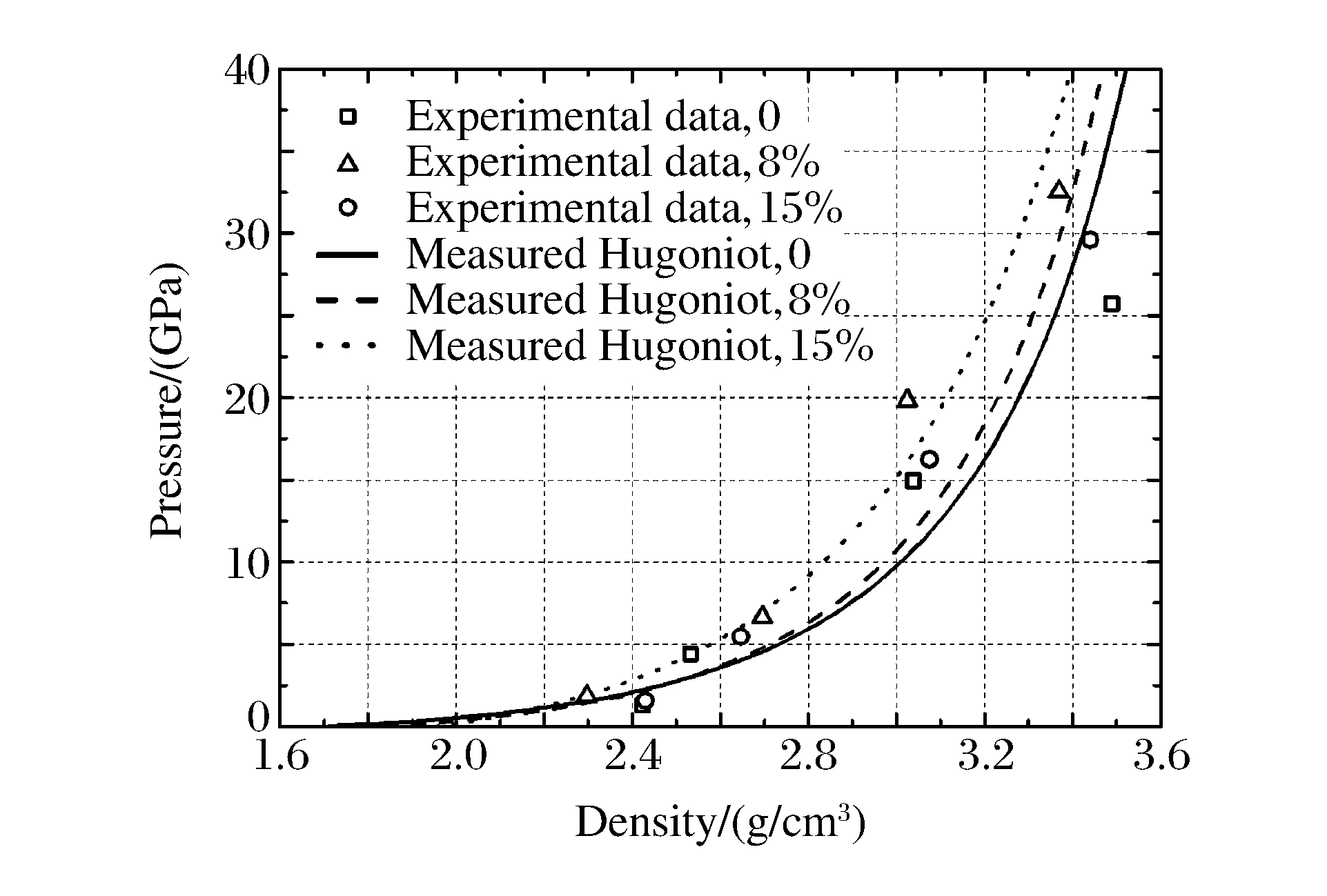
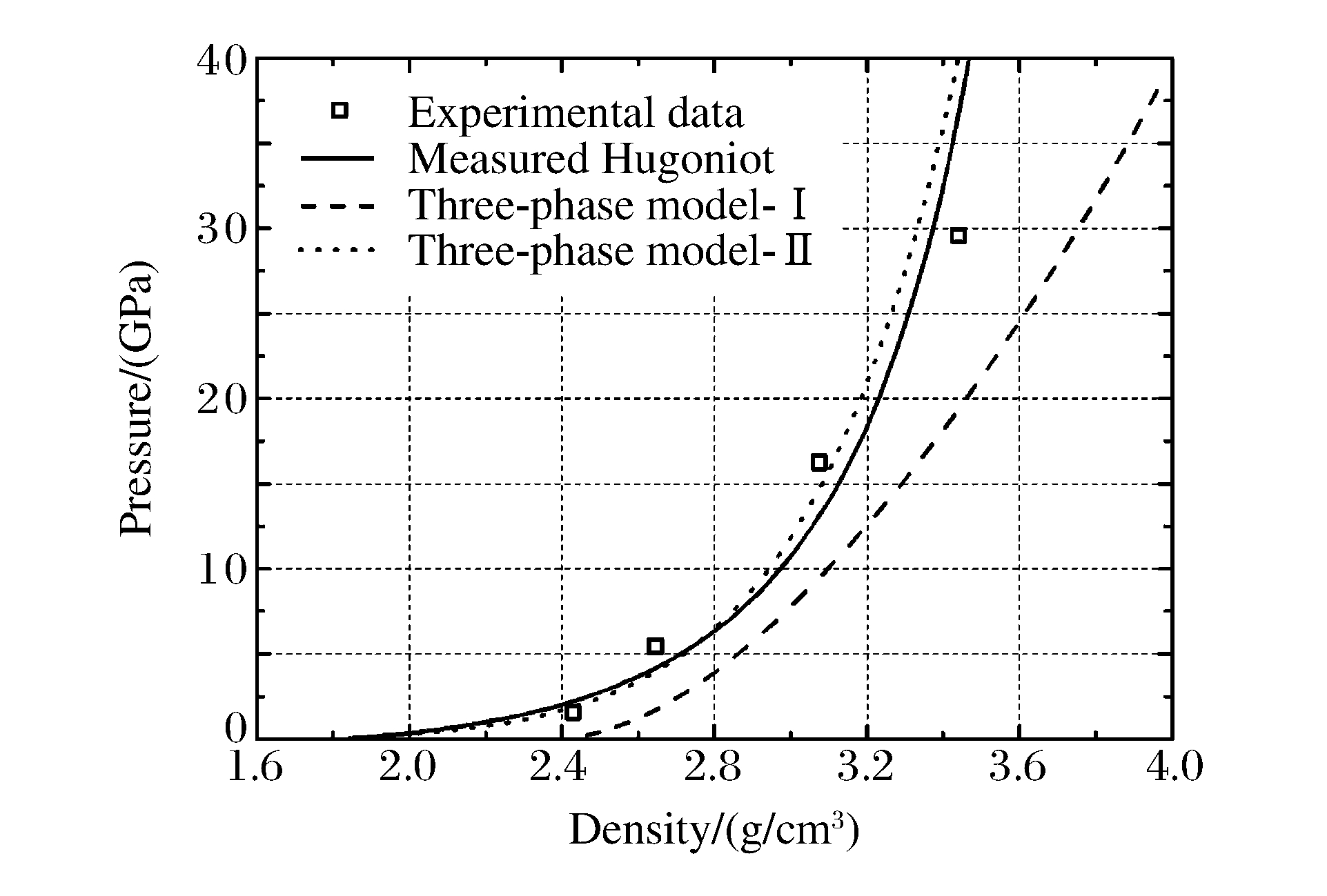
$\rho=\rho(p)=\frac{\rho_{0}}{\alpha_{\mathrm{g} 0}\left(\frac{p}{p_{0}}\right)^{-1 / k_{\mathrm{g}}}+\alpha_{\mathrm{w} 0}\left(\frac{p-p_{0}}{\rho_{\mathrm{w} 0} c_{\mathrm{w} 0}^{2}} k_{\mathrm{w}}+1\right)^{-1 / k_{\mathrm{w}}}+\alpha_{\mathrm{s} 0}\left(\frac{p-p_{0}}{\rho_{\mathrm{s} 0} c_{\mathrm{s} 0}^{2}} k_{\mathrm{s}}+1\right)^{-1 / k_{\mathrm{s}}}}$

(15)

通过与实验结果的比对发现, (15)式的描述并不准确, 与实验结果差别较大, 如图 6和图 7所示。图 6和图 7中, model-Ⅰ曲线代表(15)式描述结果, 可以看出, model-Ⅰ曲线明显低于根据实验数据拟合的曲线。故提出使用下式作为固体颗粒的状态方程

图 6 含水率为8%的试样的压力-密度关系比较

Figure 6. Comparison between experimental data and 2 three-phase EOS of clay specimen at 8% moisture content

下载: 全尺寸图片幻灯片

图 7 含水率为15%的试样的压力-密度关系比较

Figure 7. Comparison between experimental data and 2 three-phase EOS of clay specimen at 15% moisture content

下载: 全尺寸图片幻灯片

$p=p_{0}+A_{0}\left(\rho_{\mathrm{s}} / \rho_{\mathrm{s} 0}\right)^{n}$

(16)

式中:A₀=4.52 GPa, n=10.6, 是通过拟合实验数据得到的参数。

用(16)式取代(14)式, 可得修正后土的三相混合物状态方程为

(17)

将(17)式的计算结果与实验结果进行对比, 如图 6和图 7所示, 图中model-Ⅱ曲线代表修正后的状态方程。可以看出, 经过修正的三相混合物状态方程能够较好地描述黏土试样的压力-密度关系曲线, 并且能反映由含水率变化引起的非饱和黏土冲击压缩特性的变化。

4. 结论

(1) 采用二级轻气炮加载, 对3种含水率的非饱和黏土试样进行了平板撞击实验研究, 获得了3种含水率试样的冲击压缩数据。实验结果表明, 在本研究压力范围(1.29~32.54 GPa)内, 黏土试样中的冲击波速度D与波后质点速度u满足线性关系。

(2) 含水率对非饱和黏土的冲击特性影响显著, 分析表明, 在高应变率和高压力下, 滞留在黏土孔隙中的水、气体不能排出, 它们与固体颗粒组成三相介质, 共同支配着非饱和黏土的冲击压缩特性。而由于水的相对不可压缩性, 导致非饱和黏土的可压缩性随含水率的升高而下降。

(3) 针对非饱和黏土的组成特性, 提出使用三相混合物状态方程描述其压力-密度关系; 并通过与实验结果的对比分析, 提出了一种修正的固相状态方程。结果表明, 修正后的三相混合物状态方程能够更好地描述非饱和黏土的压力-密度关系。

图 1 磁测速原理示意图

Figure 1. Schematic of magnetic measurement of velocity

下载: 全尺寸图片幻灯片

图 2 平板撞击实验示意图

Figure 2. Schematic of plate impact configuration before impact

下载: 全尺寸图片幻灯片

图 3 实验测得的典型探针信号

Figure 3. Signal of fiber-optic pins measured in experiments

下载: 全尺寸图片幻灯片

图 4 黏土试样的D-u关系

Figure 4. The relationship between D and u of clay specimen at different moisture contents

下载: 全尺寸图片幻灯片

图 5 黏土试样的p-ρ Hugoniot曲线

Figure 5. The p-ρ Hogoniot curves of clay specimen at different moisture contents

下载: 全尺寸图片幻灯片

图 6 含水率为8%的试样的压力-密度关系比较

Figure 6. Comparison between experimental data and 2 three-phase EOS of clay specimen at 8% moisture content

下载: 全尺寸图片幻灯片

图 7 含水率为15%的试样的压力-密度关系比较

Figure 7. Comparison between experimental data and 2 three-phase EOS of clay specimen at 15% moisture content

下载: 全尺寸图片幻灯片

表 1 黏土试样颗粒分析结果

Table 1. Particle size distribution in the clay sample

Particle dimension/ (mm)	Mass proportion/ (%)
<0.005	28.6
0.005-0.075	71.4
>0.075	0

下载: 导出CSV

表 2 飞片材料参数

Table 2. Parameters of flyer plate materials

Material	Density/ (g/cm³)	Sound speed/ (km/s)	λ
Al alloy	2.785	5.328	1.338
Cu	8.93	3.940	1.489
Ta	16.656	3.437	1.19

下载: 导出CSV

表 3 平板撞击实验结果

Table 3. Results of plate impact experiments

Sample condition	Flyer material	Flyer velocity/ (km/s)	Shock arrival time/ (ns)	Sample thickness/ (mm)	Particle velocity/ (km/s)	Shock velocity/ (km/s)	Longitudinal stress/ (GPa)
Dry clay	Al	0.561	1 868	2.98	0.48	1.60	1.29
	Cu	1.042	1 054	2.96	0.92	2.81	4.40
	Cu	2.340	658	2.94	1.97	4.47	14.95
	Ta	3.180	556	3.02	2.79	5.43	25.71
Wet clay (Moisture content=8%)	Al	0.563	1 564	2.94	0.46	1.88	1.58
	Cu	1.101	956	2.98	0.95	3.12	5.46
	Cu	2.290	640	3.00	1.89	4.69	16.26
	Ta	3.190	500	2.94	2.74	5.88	29.60
Wet clay (Moisture content=15%)	Al	0.495	1 192	3.00	0.37	2.52	1.84
	Cu	1.142	848	2.98	0.97	3.51	6.63
	Cu	2.370	538	2.88	1.89	5.35	19.81
	Ta	3.130	478	3.01	2.64	6.30	32.54

下载: 导出CSV

参考文献(14)

[1]	Henrych J.爆炸动力学及其应用[M].熊建国, 译.北京: 科学出版社, 1987: 161-170. Henrych J. The Dynamics of Explosion and Its Application[M]. Translated by Xiong J G. Beijing: Science Press, 1987: 161-170. (in Chinese)
[2]	Tsembelis K, Proud W G, Vaughan B A M. The behavior of sand under shock wave loading: Experiments and simulations[C]//Benitez F G. Proceedings of the 14th DYMAT Technical Meeting on Behavior of Materials at High Strain Rates: Numerical Modeling. Sevilla, 2002: 193-203.
[3]	Resnyansky A D, Bourne N K. Shock compression of dry and hydrated sand[C]//Furnish M D. Shock Compression of Condensed Matter-2003. New York: American Institute of Physics, 2004: 1474-1477.
[4]	Chapman D J, Tsembelis K, Proud W G. The behaviour of dry sand under shock-loading[C]//Furnish M D. Shock Compression of Condensed Matter-2005. New York: American Institute of Physics, 2006: 1445-1448.
[5]	Chapman D J, Tsembelis K, Proud W G. The behavior of water saturated sand under shock-loading[C]//O'Brien E. Proceedings of the 2006 SEM Annual Conference and Exposition on Experimental and Applied Mechanics. Saint Louis: The Society for Experimental Mechanics, 2006: 834-840.
[6]	Chapman D J, Braithwaite C H, Proud W G. Shock-loading of statically compacted soil[C]//Elert M, Furnish M D, Cliau R, et al. Shock Compression of Condensed Matter-2007. New York: American Institute of Physics, 2007: 1367-1370.
[7]	Brown J L, Vogler T J, Chhabildaz L C, et al. Shock response of dry sand, SAND2007-3524[R]. USA: Sandia National Laboratories, 2007.
[8]	Bragov A M, Lomunov A K, Sergeichev I V, et al. Determination of physicomechanical properties of soft soils from medium to high strain rates[J]. Int J Impact Eng, 2008, 35(9): 967-976. doi: 10.1016/j.ijimpeng.2007.07.004
[9]	Arlery M, Gardou M, Fleureau J, et al. Dynamic behaviour of dry and water-saturated sand under planar shock conditions[J]. Int J Impact Eng, 2010, 37(1): 1-10. doi: 10.1016/j.ijimpeng.2009.07.009
[10]	钱七虎, 王明洋.岩土中的冲击爆炸效应[M].北京: 国防工业出版社, 2010: 205-213. Qian Q H, Wang M Y. Impact and Explosion Effects in Rock and Soil[M]. Beijing: National Defence Industry Press, 2010: 205-213. (in Chinese)
[11]	Wang Z, Lu Y. Numerical analysis on dynamic deformation mechanism of soils under blast loading[J]. Soil Dyn Earthq Eng, 2003, 23(8): 705-714. doi: 10.1016/S0267-7261(03)00076-9
[12]	Wang Z, Hao H, Lu Y. A three-phase soil model for simulating stress wave propagation due to blast loading[J]. Int J Numer Anal Met, 2004, 28(1): 33-56.
[13]	汤文辉, 张若棋.物态方程理论及计算概论[M].第2版.北京: 高等教育出版社, 2008: 293-295. Tang W H, Zhang R Q. Introduction to Theory and Computation of Equations of State[M]. 2nd ed. Beijing: Higher Education Press, 2008: 293-295. (in Chinese)
[14]	王荣波, 田建华, 何莉华, 等.石英光纤探针在非金属材料冲击实验中的应用[J].爆炸与冲击, 2006, 26(3): 284-287. Wang R B, Tian J H, He L H, et al. Application of fiber-optic pin to nonmetallic shock experiments[J]. Explosion and Shock Waves, 2006, 26(3): 284-287. (in Chinese)