Experimental Research of Deflagration to Detonation Transition of Epoxypropane-Aluminum-Air Mixtures in Large-Scale Tube
-
摘要: 在长为32.4 m、内径为0.199 m的大型长直水平管道中,对环氧丙烷-空气两相流云雾及环氧丙烷-铝粉-空气三相流云雾的爆燃转爆轰(DDT)过程进行了实验研究。对弱点火条件下多相混和物DDT过程的不同阶段特征进行了分析,对比研究了不同浓度时混和物的燃爆情况。结果表明:浓度为513 g/m3的环氧丙烷-空气混和物及浓度为237和643 g/m3的环氧丙烷-铝粉-空气混和物均能在管道中完成爆燃向爆轰的转变,进入自持爆轰阶段,其胞格尺寸分别为0.28和0.50 m。Abstract: Motivated by the current interest in the mechanism of the deflagration to detonation transition (DDT), the DDT experiments of epoxypropane-air mixture and epoxypropane-aluminum-air mixture are carried out by a large-scale tube (32.4 m long and 0.199 inner diameter). The processes of DDT in multi-phase clouds are analyzed, and the mixtures with different concentrations are compared. The self-sustained detonation waves are formed in the epoxypropane-air mixture with epoxypropane concentration of 513 g/m3 and epoxypropane-aluminum-air mixture with epoxypropane and aluminum concentrations of 237 and 643 g/m3, and moreover the cell size of the detonation are 0.28 and 0.5 m, respectively.
-
Key words:
- deflagration to detonation transition /
- weak ignition /
- epoxypropane /
- aluminum /
- self-sustained
-
现代化国防军工和航空航天等国家战略领域的发展与先进材料的进步密不可分。在轻量化、高性能等要求下,陶瓷材料扮演着十分重要的角色。陶瓷材料通常具有高熔点、高硬度、高比强度、高耐磨性和耐氧化等优异的物理和力学特性,在恶劣的服役环境中,如航空航天设备、空间站设备、卫星器件、车辆装甲乃至单兵盔甲防护等领域[1-3],具有得天独厚的优势,拥有广阔的发展前景。与此同时,极端服役环境中常见的高温、高压、高应变率现象也催生了对重要工程材料在动态荷载下的物理和力学性能研究。事实上,材料或结构的冲击动力学行为研究自第二次世界大战以来空前活跃,相关研究也日益深入。发展至今,人们对许多材料在动荷载下的响应研究都形成了一定的积累。然而,这些研究受各时期社会工业技术水平、实验技术手段、计算模拟方法以及高性能计算机发展等的限制而存在一定的不足。随着人类在地表活动范围的扩大以及向外太空探索能力的提高,对地球内核、外太空星系物质以及未来能源的研究更加迫切,对极端高温高压和高应变率现象的研究兴趣与日俱增。(超)高速碰撞行为、(超)高应变率现象广泛存在,例如高速行驶汽车及高铁的碰撞、装甲的侵彻、航空航天飞行设备的碰撞、星际物质的碰撞以及各种类型的爆炸[4-6]等。冲击或碰撞速度可达每秒数百米甚至数千米,在太空环境中更高,能够达到10 km/s以上[5-6];服役环境温度可从数百摄氏度增加到上千摄氏度甚至更高。实现极端条件(如高压、高温、高应变率或高速率)的加载方式包括多级轻气炮[7-8]、磁驱动装置[9]、激光驱动发射装置[10-13]等,例如:美国圣地亚国家实验室的磁驱动Z机器[14]、中国工程物理研究院的磁驱动装置CQ系列[15]、美国国家点火装置(NIF)[16]以及中国工程物理研究院的“聚龙一号”[17]和“神光Ⅲ”[12]等装置。其中:霍普金森压杆装置和轻气炮驱动的平板冲击装置是最常见的动态加载实验设备,可实现每秒数十米至数千米的高速发射,常用于研究应变率为106 s−1以下的问题;而激光脉冲加载装置可实现107 s−1以上的高应变率加载。在这些极端高速加载或高温高压和高应变率荷载作用下,材料的物理和力学性质往往会发生显著改变[18-19]。利用不同的动态实验设备可实现材料在动态压缩下的弹性、塑性以及相变研究。这些压缩变形行为又对材料的损伤演化和破坏行为特征产生深远影响,尤其是冲击与爆炸荷载在材料内部产生的应力波效应,使得整个动态物理力学过程变得更加复杂。
外部加载条件影响着材料的动态响应,材料本身的微观结构则从根本上决定了材料的物理和力学特性。碳化硅(SiC)晶体由碳、硅两种原子有序排列组成,由于原子层不同的堆积方式,形成了超过250种SiC多型[20]。常见的六方(Hexagonal)SiC包括2H、4H以及6H多型等,被称为α-SiC;3C-SiC作为唯一的立方(Cubic)多型,也被称为β-SiC。6H-SiC是工业生产中应用最广泛的晶型。众所周知,材料的变形、损伤和破坏是典型的跨尺度物理和力学问题。变形与破坏起源于纳观尺度下原子的移动和原子间化学键的断裂。损伤破坏过程中,随着点缺陷的形成和发展,逐渐形成纳米孔洞或纳米裂纹,而这些纳米孔洞或裂纹的进一步生长和扩展最终形成宏观破坏,导致材料失效。对晶体材料而言,完美的晶体材料如单晶体可充分体现物质本身的特性,而含缺陷的晶体材料如多晶体则表现出微纳米缺陷结构对材料宏观物理和力学性质不可忽略的影响。陶瓷材料中晶体的结构和键合方式决定了其具有很高的抗压强度和硬度,但缺陷的存在导致其抗拉和抗剪切强度显著降低,并常常表现出明显的脆性,特别是传统工程陶瓷,由于工艺限制往往含有大量缺陷及不同程度的杂质,包括主晶相、玻璃相和气相,使其组织结构十分复杂。这在很大程度上限制了主晶相陶瓷材料性能的发挥,也是传统工程陶瓷材料的实际强度与理论强度跨量级差异的主要原因。随着工艺和技术的发展,被视为先进材料的硬质单晶及纳米陶瓷和具有特殊微结构的新型陶瓷逐渐兴起,相比传统工程陶瓷,具有更优异的物理和力学性能。根据结构是否存在晶界,材料可分为单晶和多晶SiC,其中硬质单晶是指整体晶面空间取向完全一致的陶瓷晶体,原子结构排列长程有序;而纳米多晶陶瓷则是指陶瓷材料的显微结构中,晶粒、晶界以及两者之间的结合都处在纳米水平。纳米结构有望使材料的强度、韧性和超塑性等显著提高,并对材料的电学、热学、磁学和光学等性能产生重要影响,可以弥补传统工程陶瓷的诸多不足。
材料动态行为研究中加载条件的多样性与陶瓷材料微结构的复杂性共同决定了陶瓷材料动力学问题的复杂程度和面临的诸多挑战。因此,陶瓷材料的动力学问题是涉及多因素影响且多因素高度耦合的跨多个时间和空间尺度的复杂科学问题。
由于陶瓷材料种类繁多,且各种陶瓷材料的动力学行为研究工作量庞大[21-27],本文仅以SiC的动态响应和微结构对变形与破坏机理的影响为主线,结合相关材料的物理和力学性质以及本课题组近些年开展的SiC相关研究工作,从不同研究手段和时空尺度对不同加载条件和微结构下SiC的变形、损伤和破坏研究进展进行回顾、梳理和总结,并对后续研究进行展望,以期为相关领域的研究人员提供一定的参考。
1. SiC动态力学性能实验
SiC等陶瓷材料的动力学研究历史丰富,时间跨度大,为便于分析和总结,以实验手段为主线梳理相关研究进展,突出不同动态实验装置的特点及时空尺度研究范畴。
1.1 抗弹性能和动态破碎实验
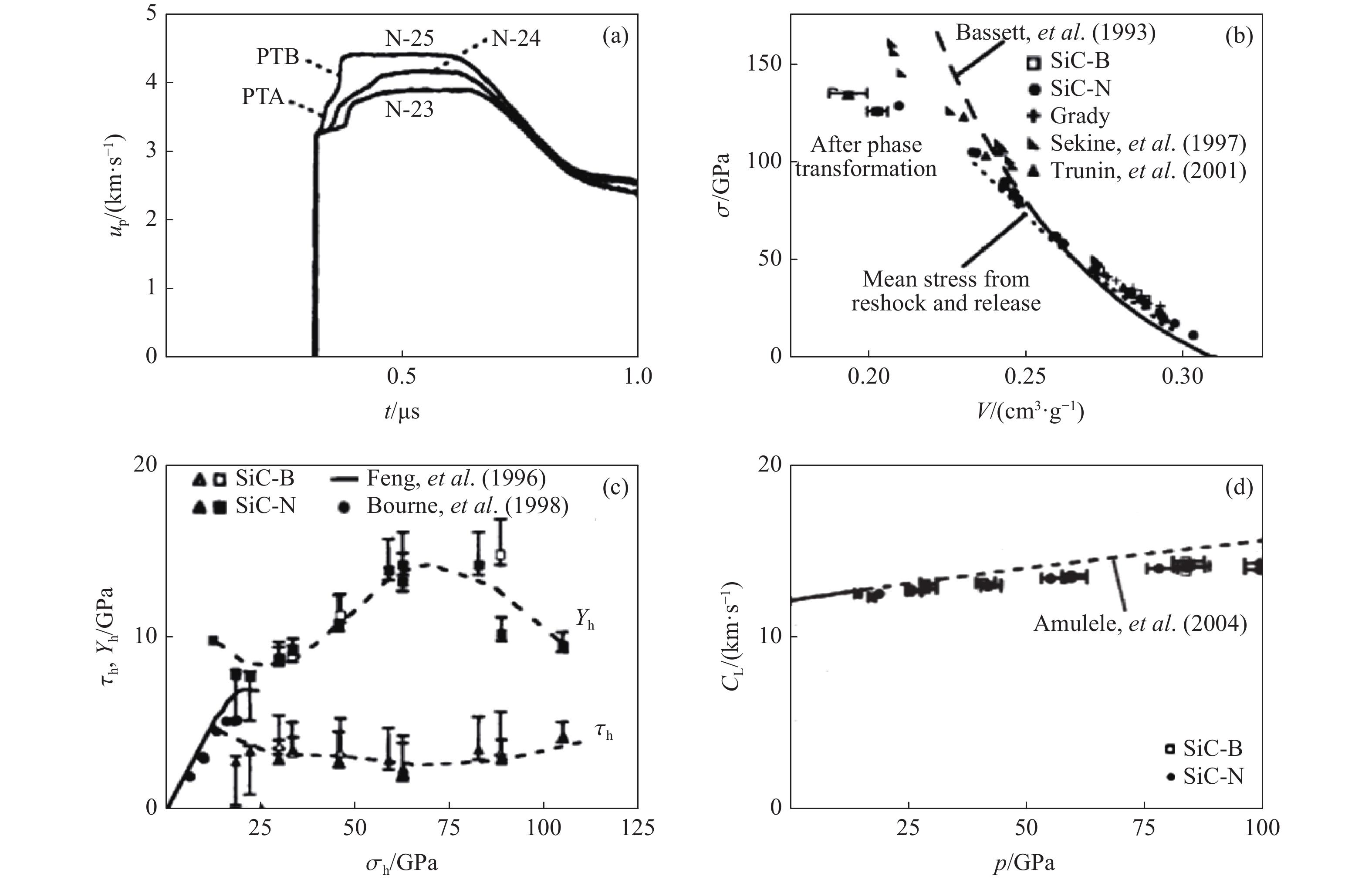
陶瓷类材料具有硬度高、密度小的优点,对子弹头和破碎弹片等具有很强的防御和抗侵彻性能。大量文献阐述了陶瓷及其复合材料的弹道破坏和抗侵彻机理[28-31]。王长利等[32]进行了爆炸成型弹丸对氧化铝、SiC及碳化硼装甲陶瓷材料的侵彻深度实验,得到了装甲陶瓷材料在3 km/s侵彻速度下的质量防护因数和差分防护因数。Subhash等[33]发表了陶瓷压痕和冲击损伤分析模型的研究综述,并对B4C、ZrB2-SiC、SiC陶瓷在动态压痕及高速冲击下的变形及断裂演化进行比较,证实了动态压痕研究可以捕获陶瓷材料在弹道冲击下发生的结构相变。Normandia[34]通过碳化钨球体冲击热压和烧结的SiC靶板,研究了冲击速度为1.7 km/s的SiC弹道响应过程,其中SiC的弹道响应曲线表现出与金属相似的特征。高于穿透发生速度和低于穿透器变形的球体冲击数据代表了实验的临界区域。随着冲击速度提升,靶板依次表现出无宏观变形、形成弹坑、弹坑逐渐扩大以及弹道响应曲线形状改变。Li等[35]通过实验和数值方法研究了碳纤维增强SiC复合材料(C/SiC)在低速(150 m/s)侵彻过程中的动态响应和断裂机制。实验观察到,当弹丸接触目标靶板时,周围孔洞由于应力集中产生裂缝,并伴随整个侵彻过程,且在穿透过程中,弹丸的强烈振动会产生额外的应变率。王鹏[36]通过SiC陶瓷抗穿甲模拟弹试验,研究了SiC陶瓷与均质装甲钢组成的复合结构的几种抗弹效应,发现其防护性能优于相同面密度下的均质钢靶板和氧化铝钢复合靶板。Zinszner等[37]通过垂直面板冲击和边沿冲击两种方式研究了SiC的动态破碎行为。Forquin等[38]对4种不同工艺制备的存在微结构差异的SiC开展了动态破碎行为研究,重点分析了微结构在破碎过程中的主要影响因素,并指出陶瓷的冲击响应主要取决于微结构中散布的缺陷数量(见图1)。冲击后的试样中大量由环向拉应力引起的径向裂纹与环向裂纹正交连接。可以看出,SiC具有良好的抗弹性能,但其动态破碎行为受到材料微结构的影响显著(见图2)。
1.2 基于霍普金森压杆的动态实验
分离式霍普金森压杆(SHPB)是材料动态研究中最常见的装置之一,应变率范围多在103~104 s−1之间,可开展材料在一维应力状态下的动态响应研究[39]。早期SHPB多用于测试可产生较大塑性变形的金属,以研究动态力学行为及本构关系[40-41]。针对脆性材料的霍普金森杆实验技术面临的诸多问题,人们对霍普金森杆技术进行了改良[42]。Ravichandran等[43]对使用SHPB测试硬度较大的陶瓷材料的试验技术给出了修改建议,并指出陶瓷样品使用SHPB加载获得的最大应变率受到样品长度以及材料失效应变的限制。Shih等[44]基于SHPB对两种热压烧结α-SiC(B掺杂SiC和Al掺杂SiC)的动态变形与损伤演化进行了研究,发现两种SiC的失效模式差异显著,前者为穿晶断裂,后者为晶间断裂并伴随更高的断裂韧性,同时观测到堆叠层错和位错形式的塑性变形证据,但位错仅在Al掺杂SiC中存在。Shih等[44]讨论了材料初始失效的若干机理:晶界脱粘、孔洞、位错堆积引起应力集中产生的萌生裂纹、堆叠层错和晶体多形体引起的晶界应力集中以及弹性各向异性引起的膨胀裂纹。Sarva等[45]利用SHPB研究了SiC的动态抗压强度,发现压缩强度在应变率大于102 s−1时显著增大,但失效模式仍相似,均为破碎失效。Bourne等[46]和Pickup等[47]利用SHPB实验研究了具有相似密度和晶粒尺寸但材料制备工艺不同(反应烧结、热压烧结、无压烧结)的3种SiC材料的动态响应,其应变率为103 s−1,伴随的压应力脉冲约为200 μs。结果显示,3种SiC材料的动态力学行为差异明显,与准静态相比,材料的压缩强度在高应变率下增大,但不同材料的应变率敏感度不同,制备方法不仅导致材料抗冲击强度的差异显著,还改变了材料的失效形态。这说明不同制备工艺引入的微结构差异对SiC的力学特性具有重要的影响。Wang等[48]使用SHPB装置研究了热压SiC的动态强度和碎裂,测量了加载速率对单轴压缩强度的影响,如图3所示,压缩失效强度在高加载速率时显著增强。热压SiC陶瓷中的裂纹在应力强度因子达到某临界值之前通常表现出亚临界裂纹扩展特征,即在达到临界外荷载作用下裂纹起裂并在失稳前稳定扩展。热压SiC材料的亚临界扩展过程较短,在裂纹起裂后荷载的增加即刻引起失稳扩展,从而导致材料失效。因此,在较低的加载速率下,这种亚临界裂纹扩展成为了SiC陶瓷压缩强度不存在率效应的原因。当加载速率较高时,动态增长裂纹的惯性效应对微裂纹的传播起到抑制作用,因而可承受更高荷载,从而提高了陶瓷的动态抗压强度。研究还发现,低加载速率下的抗压强度指数与基于断裂力学所得的亚临界裂纹增长对应的应力强度指数相近,表明亚临界裂纹扩展主导了低加载速率对压缩强度的影响,而惯性效应是高加载速率下产生率效应的主要原因。
靳晓庆[49]对包括SiC在内的陶瓷材料开展了基于SHPB装置的冲击压缩荷载作用下的动态破碎实验研究。结果显示,材料强度的应变率相关性显著,即加载应变率越大,试样的抗压强度越高,但试样的密实度对强度的影响极大。同时,材料的破坏机理也随着加载条件不同发生变化,分析认为动态破坏中试样的破坏是内部微裂纹多处起裂扩展汇聚引起的。孙红婵等[50]基于SHPB系统对钨丝掺杂SiC和SiC材料进行了高速冲击力学性能试验,观察到钨丝的塑性促进了SiC材料的塑性变形。高远飞[51]也对包括SiC在内的陶瓷材料开展了SHPB压缩强度测试。Wang等[52]基于SHPB研究了热压烧结SiC在动态压缩下的非弹性变形和最终的穿晶断裂,并利用SEM和透射电镜(TEM)观测回收碎片,发现宏观的非弹性行为是由位错运动和局部无定形化主控的,如图4所示。Li等[53]利用SHPB研究了遭受热冲击后的SiC的动态力学行为,结果表明:加热温度为100 ℃时,材料的压缩强度基本没有变化;加热温度高于200 ℃时,压缩强度明显降低。
综合以上基于SHPB装置开展的SiC动态力学行为研究发现,SiC陶瓷的动态抗压强度受到应变率的影响,一般在高于102 s−1时随着应变率的增加而增大,但抗压强度对微结构变化极为敏感,同时也一定程度受到高温的削弱作用。
1.3 基于轻气炮的平板冲击实验
轻气炮是重要的动态加载实验装置,可以开展材料在一维应变状态下的动力学特性研究,实现比SHPB更高的压力和应变率加载,应变率范围主要集中在104~106 s−1,在材料的高压和高应变率研究中发挥了重要作用。
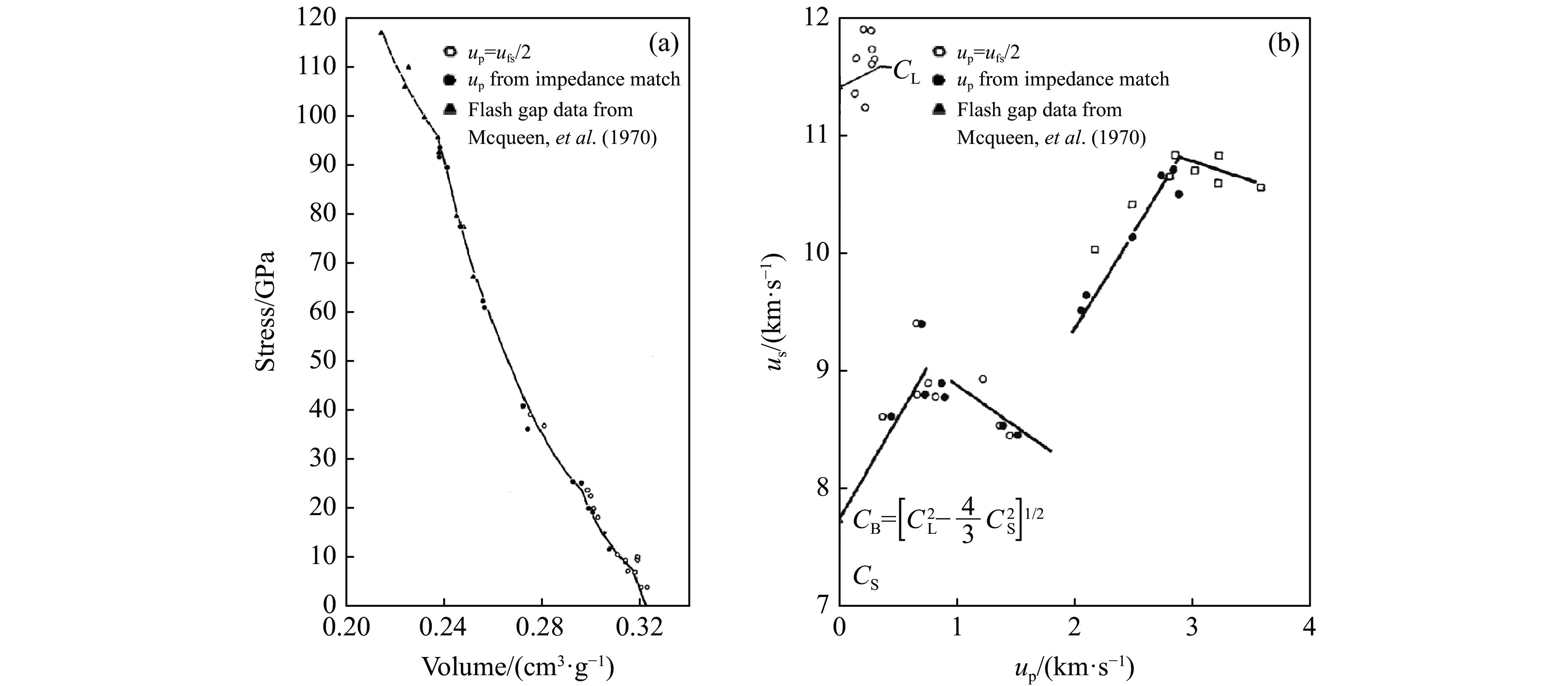
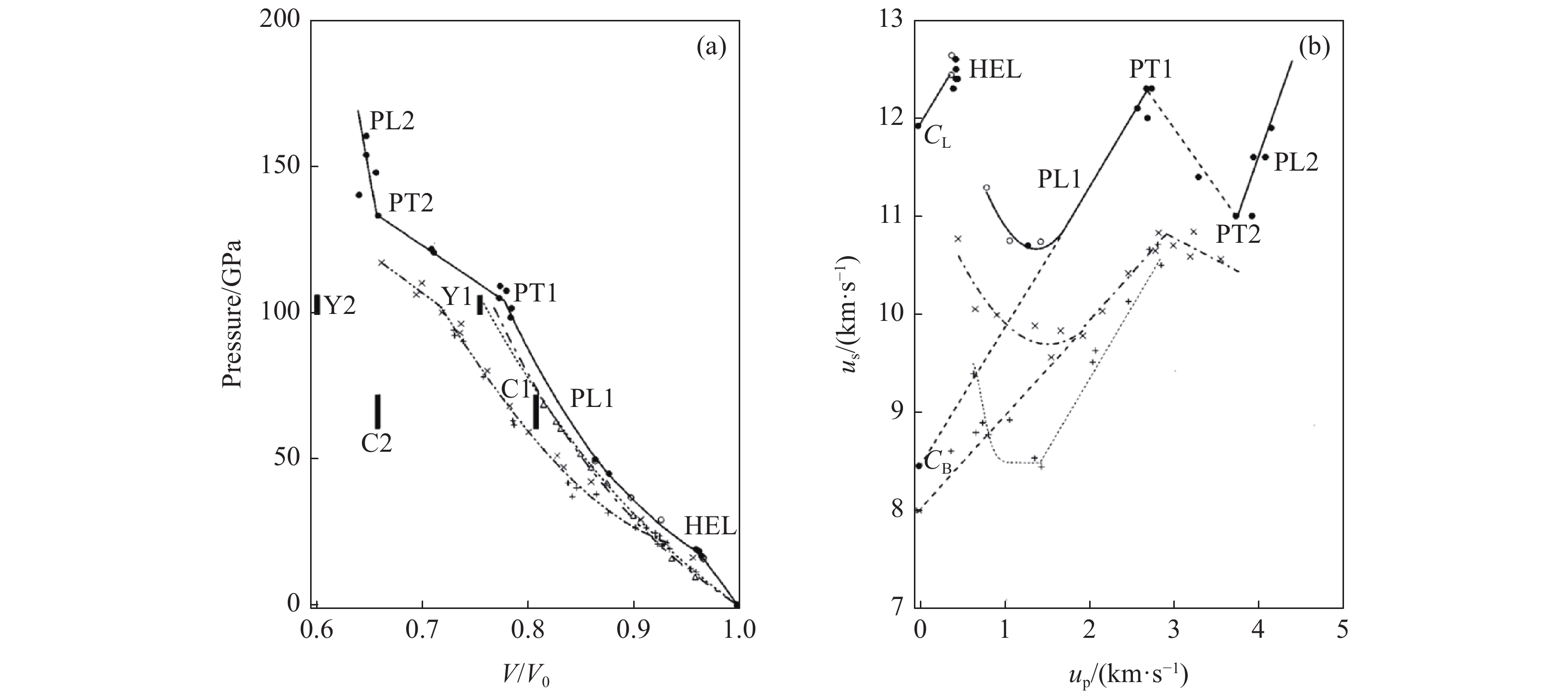
脆性固体材料的冲击波问题研究可追溯至早期对岩石、矿物[54]和陶瓷材料[55-58]的研究。通过这些工作,人们获得了大量材料的压缩强度信息,包括弹性雨贡纽极限(Hugoniot elastic limit,HEL)和Hugoniot曲线等。其中,Gust等[56]根据测得的Hugoniot曲线的不连续性,计算得到SiC的HEL为8 GPa,并判断在24和96 GPa下SiC存在两种相变,如图5所示。图中:us为冲击波速度,u
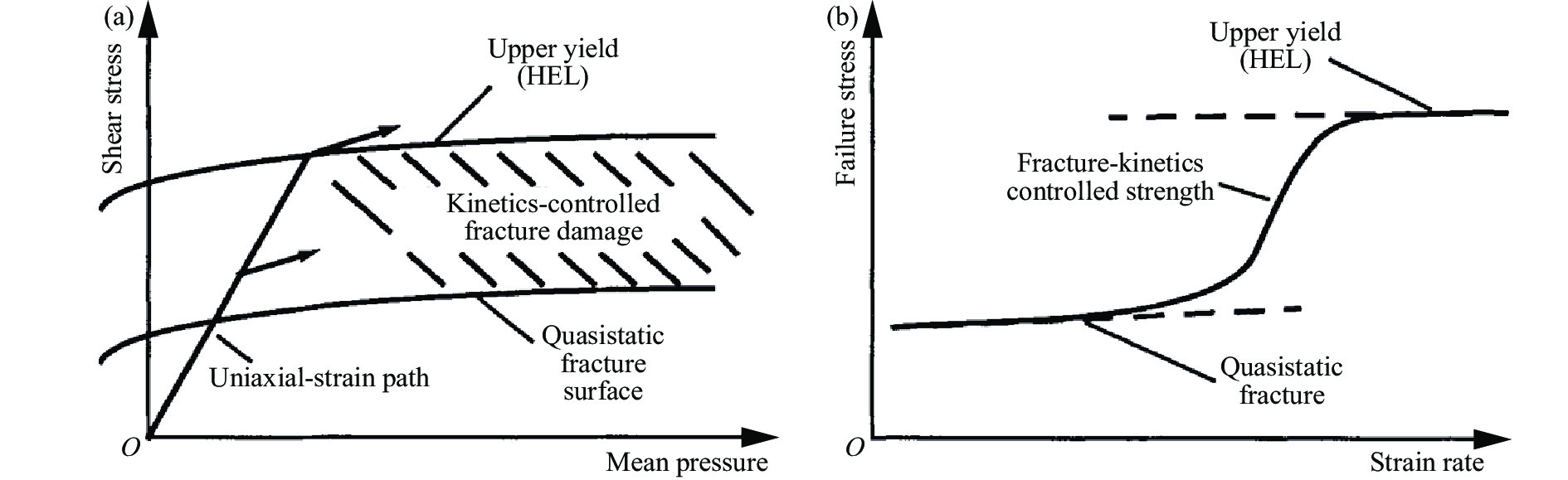
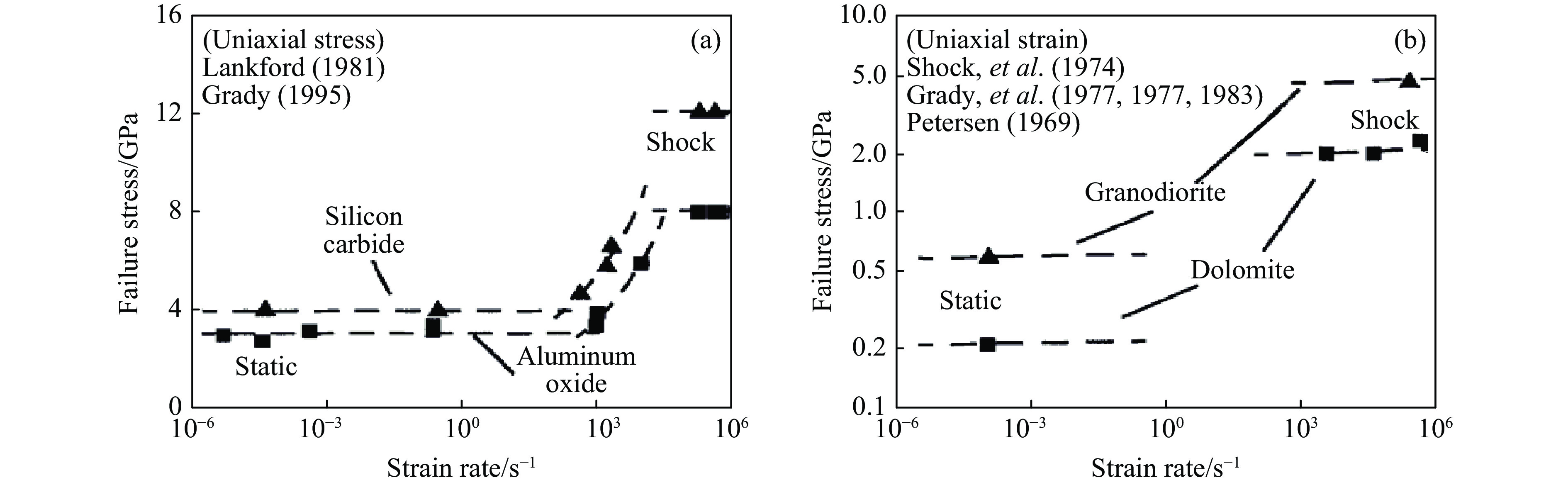
p为粒子速度,u fs为自由面速度,CL为纵波波速,CS为剪切速度,CB为平均速度。Gust等[56]认为,获得的SiC Hugoniot曲线和冲击波速-粒子速度曲线拐点预示着相变的发生,低压相变点对应于晶体硅类似的相变。 然而,Grady[59]在实验中采用平面冲击方法和速度干涉测量诊断技术获得了SiC陶瓷等脆性材料的高分辨率冲击剖面数据,测得SiC的HEL为15 GPa,但并没有SiC在较低应力下的相变报道。Grady[59]基于多项冲击波的历史数据判断SiC等脆性材料存在失效波,并指出在这些材料的动态失效过程中,晶体塑性和脆性断裂扮演着重要角色并相互关联,如图6所示。图6(a)显示了剪应力与压力的关系,可见其中有两种完全不同的失效平面,下平面是准静态断裂极限,上平面为冲击压缩屈服平面(HEL)。图6(b)则给出了材料失效强度与压缩应变率的关系。当压缩应变率很低时,强度主要由断裂控制;在中压缩应变率区间,强度则由热激活的亚临界裂纹生长控制;而在高压缩应变率下,则激活了另一种损伤失效。这种趋势被解读为压缩应变率相关的脆性到延性转变失效机理。图7展示了损伤动力学控制的材料失效强度的临界压缩应变率以及更高压缩应变率区间应变率不敏感的失效机理。
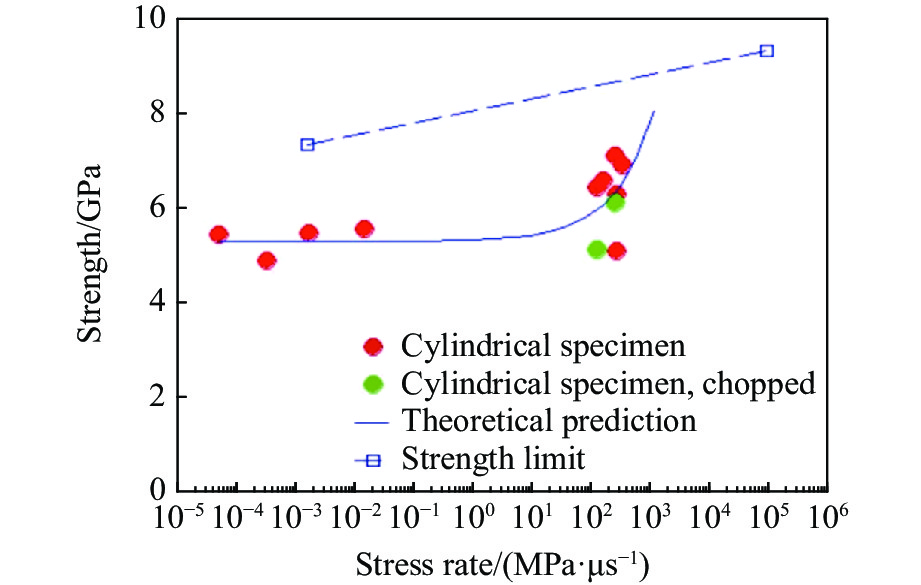
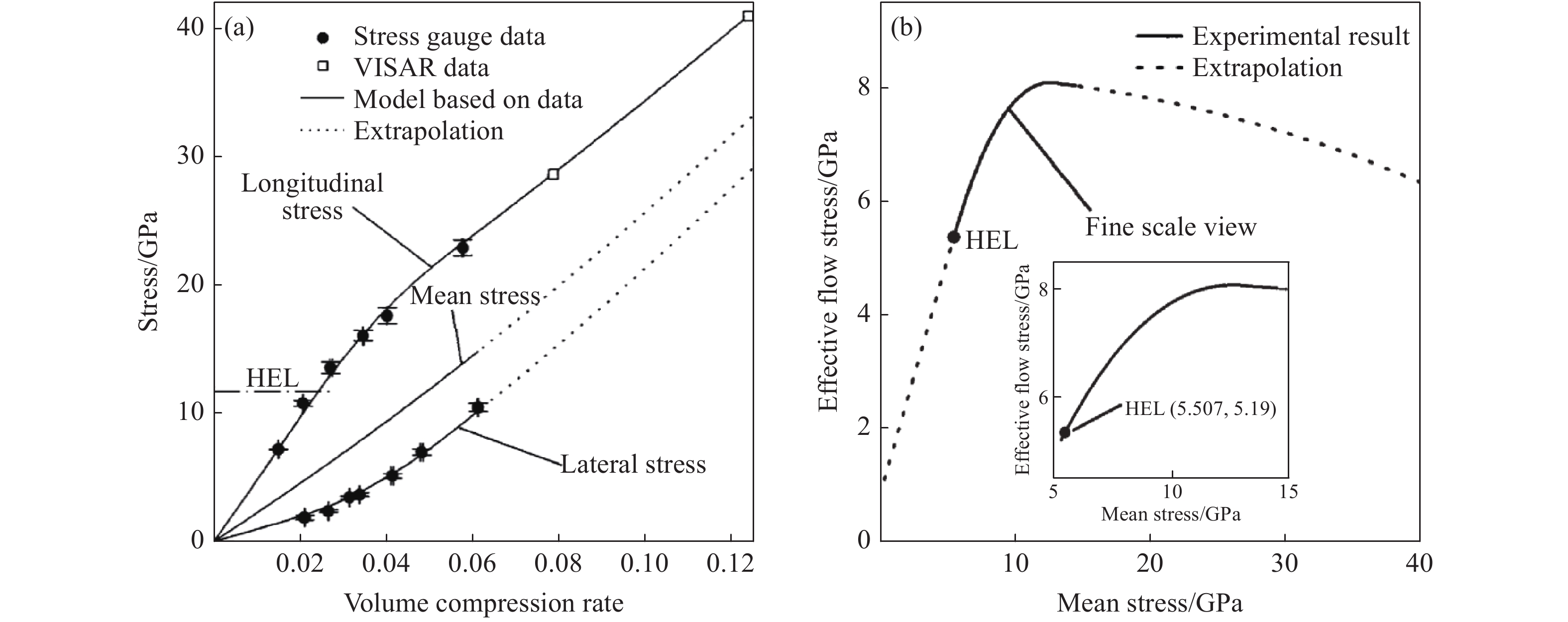
Feng等[60]研究了多晶SiC在7.3~23.0 GPa冲击压力范围的冲击响应,发现当HEL超过11.7 GPa时,SiC呈现伴随分散波阵面的非弹性响应,并且指出由于HEL测量数据的离散性,HEL可能不是评价材料在冲击状态下强度的最合适参量,但可能是描述材料从孤立的微观损伤向宏观屈服或失效过渡的指标。在该研究组另一项多晶SiC的冲击研究[61]中,加载应力在10~24 GPa范围内,如图8所示,研究结果表明:冲击载荷下SiC具有极高的强度,最大剪切应力可以从HEL(11.5 GPa)时的4.5 GPa增加到两倍HEL应力时的7.0 GPa,压力高于两倍的HEL后,材料逐渐软化。冲击作用下SiC中的弹性-非弹性过渡并不明显。超过HEL时的材料强度演化既不像由大量裂纹引起的崩塌式失效,也不像典型的塑性响应。他们认为,该结果是晶粒间微弹性和高度约束下微裂纹的非均匀变形造成的。值得一提的是,该工作没有发现Bourne等[46]报道的失效波现象,并指出失效波的发生可能与材料制备工艺有关,即与材料微结构的差异相关。Yuan等[62]在冲击压剪实验中发现:在弹性响应区间,SiC材料的泊松比从0.161增加至HEL压力时的0.192;高于弹性极限时,SiC的最大剪切应力从4.5 GPa增加到6.4 GPa,对应的冲击荷载峰值应力为18 GPa。
可以看出,尽管这些研究均基于轻气炮的平板冲击实验,但是不同学者获得的SiC HEL存在显著差异(差异范围在8~15 GPa之间),反映了不同SiC试验材料的微结构存在差异。通常而言,材料的HEL与其微结构特征(如纯度或杂质比例、密实度、孔隙率等)密切相关。以上研究采用的SiC试样的生产年份跨度大,供应商和工艺水平也有所不同,导致材料的HEL存在差异。此外,大部分SiC冲击响应实验的加载压力有限,仅Sekine等[63]采用两级轻气炮和光学方法直接测量得到冲击压力高达160 GPa下的6H-SiC的冲击波速度和粒子速度,如图9所示。在他们的研究中,SiC的HEL为17~19 GPa,探测到的冲击相变压力在(105 ± 4) GPa水平,相变对应的体积减少约(15 ± 3)%。该体积变化预示着高压相具有六阶配位数,并且极可能是岩盐结构。Zhu等[64]基于一级轻气炮回收实验对立方SiC的冲击相变进行了研究,通过X射线诊断回收试样,发现了3C、6H和15R等不同晶体结构之间的相变:随着冲击压力和温度的增加,
α -SiC的15R结构增加而6H结构减少;与此同时,小部分的α -SiC转变为3C结构,而β-SiC则转变为15R结构。从两种SiC的冲击相变结果上看,似乎是冲击下更倾向变化为15R结构。他们进一步对冲击压力和温度以及不同结构相变的非均匀分布进行了详细讨论,分析指出这些不同结构相变归因于SiC原子层堆叠序列的变化,但后续没有进一步研究报道。如图10所示,Vogler等[65]基于一系列时间分辨平板冲击实验,研究了两种工艺制备的六方SiC在冲击应力高达140 GPa时的冲击响应,获得了Hugoniot曲线,利用再冲击和卸载装置研究了再加载和卸载响应,为量化SiC材料的剪切应力和测量Hugoniot状态下的强度提供了一种方法。该研究发现:立方SiC的冲击相变压力约为104 GPa,伴随着约9%的体积改变;在低于此压力情况下,初始卸载过程中依旧呈现弹性响应,再加载时也遵循该路径,该力学行为完全不同于碳化硼和氧化铝等陶瓷材料;随着冲击压力逐渐接近相变阈值,在50~75 GPa的压力区间,SiC的强度增加了约50%,随后下降。与Feng等[60-61]的研究工作不同的是,该研究中当冲击压力高于HEL时,剪应力趋于稳定而非增加。平板冲击下SiC的强度变化一定程度上表现出与金属类似的特征。
Paris等[66]的研究发现SiC的动态压缩失效具有两种机制:当横向应力低于某临界应力(1.5 GPa)时,压缩失效压力阈值与横向应力具有较强的关联性;而当横向应力高于该临界值时,则表现为明显较弱的相关性。研究指出,在该临界值附近,低横向应力时主导非弹性变形的脆性纹裂将让步于一定程度的延性屈服,说明侧限对材料的影响显著。横向应力增加可为材料失效从脆性向延性转变创造条件。SiC的这种特性与其他陶瓷如碳化硼等完全不同。Gautam等[67]使用平板冲击方法测定了SiC等轻质陶瓷的冲击状态方程,压力范围为20~100 GPa,并测得SiC样品的HEL为13.27 GPa。他们在报告中也提到了陶瓷材料在冲击载荷下的延迟失效现象。Bourne等[46]和Millett等[68]对不同技术生产的3种等级的SiC进行了平板冲击实验,发现当平板冲击达到最大应力后,受冲击的SiC也存在延迟失效现象。
传统工程陶瓷的冲击压缩研究表现了其高抗压强度,而断裂破坏研究则反映出其抗拉伸性能的不足。冲击层裂是陶瓷材料动态断裂研究的重要问题。Winkler等[69]研究了SiC等多种陶瓷在平面冲击实验中的层裂行为,发现当冲击压力低于HEL(13.0~14.7 GPa)时,随着冲击压力增大,SiC的层裂强度首先从0.58 GPa增大至1.07 GPa,然后降低至0.48 GPa(对应的冲击压力为12.1 GPa);当冲击压力超过HEL时,层裂强度再次增加至0.7 GPa(对应的冲击压力为19.6 GPa)。与Winkler的结论不同,Bartkowski等[70]对两种SiC陶瓷(热压和烧结制备)开展了冲击层裂实验,冲击压力低于HEL(约12 GPa),实验结果显示,两种SiC陶瓷具有相似的变化趋势:在冲击应力从1.6 GPa增加到3.7 GPa的过程中,层裂强度逐渐增大;而冲击应力达到3.7 GPa以上时,层裂强度开始变小。不同工艺制备的两种SiC的层裂强度也有所不同,热压SiC的层裂强度为0.83~1.30 GPa,而烧结SiC的层裂强度仅为0.27~0.97 GPa。这主要归因于工艺不同引起的微结构差异,热压SiC具有更高的密度,平均晶粒尺寸为1.9~2.2 μm,而烧结SiC的密度相对更低,平均晶粒尺寸为15 μm。Dandekar等[71]在平面冲击实验中(最大冲击应力为17 GPa),对5种不同类型的SiC材料的拉伸强度进行了测量,对比发现,不论材料制备工艺如何,都存在一个临界冲击压力,使得冲击荷载低于该临界压力时层裂强度随着冲击压力的增加而增大,高于该临界压力时则开始减小。Dandekar[72]还研究了压缩和压剪冲击波载荷下SiC的层裂强度,结果表明:烧结和热压SiC的层裂强度仅在0.24~1.23 GPa范围内,且层裂强度的变化存在两个阶段,即冲击应力小于4 GPa时呈增大趋势,而冲击应力大于6 GPa时呈减小趋势。这种不寻常的趋势被认为是局部塑性发展和裂缝的产生和扩展两种机制竞争作用的结果。上述研究结果均表明影响SiC层裂的因素很多。在低压缩应力下,放电等离子烧结(SPS)工艺处理的SiC层裂强度几乎是恒定的[73],仅在1.4~1.5 GPa区间出现微小变化,对应的峰值冲击压力从2 GPa增大至5 GPa,但是在冲击应力为21.5 GPa时,该SiC材料的层裂强度单调降低至约0.34 GPa。Savinykh等[74]研究了不同厚度(0.5~8.3 mm)SiC试样的冲击波传播特性,从自由面粒子速度时程曲线中并未发现弹性前驱波衰减现象。在较薄的试样中,由于冲击后表面的卸载波比压缩波再反射到达的时间晚,实验中并没有观察到层裂现象。而当样品厚度为8.32 mm时,层裂强度为0.62 GPa;样品厚度为3.81 mm时,层裂强度为0.5 GPa。在该研究中,SiC陶瓷的HEL仅为8.72 GPa,且样品厚度对其没有直接影响,其较低的HEL主要是密度低(仅为3.065 g/cm3)引起的。统计发现,HEL受样品密度的影响很大,当密度在3.06~3.24 g/cm3范围内变化时,SiC的HEL在8~16 GPa区间变化。Garkushin等[75]研究了3种反应烧结SiC陶瓷在3~19 GPa冲击应力范围内的动态强度,发现层裂强度在冲击应力为HEL的一半时达到最大,随后在接近HEL时显著降低甚至下降至零,然而当冲击压力进一步提升后却观测到层裂强度增大。对比以上学者的研究结果可见,该结果既呈现了与Bartkowski等[70]和Dandekar等[71]类似的现象,即层裂强度在低于HEL的某个冲击压力时达到最大而后降低,还观测到与Winkler等[69]相似的结果,即冲击压力高于HEL时SiC的层裂强度不为零。压缩应力接近HEL时层裂强度的急剧下降可能是由材料孔隙附近的微裂纹、孔隙以及材料中的低模量杂质导致的。
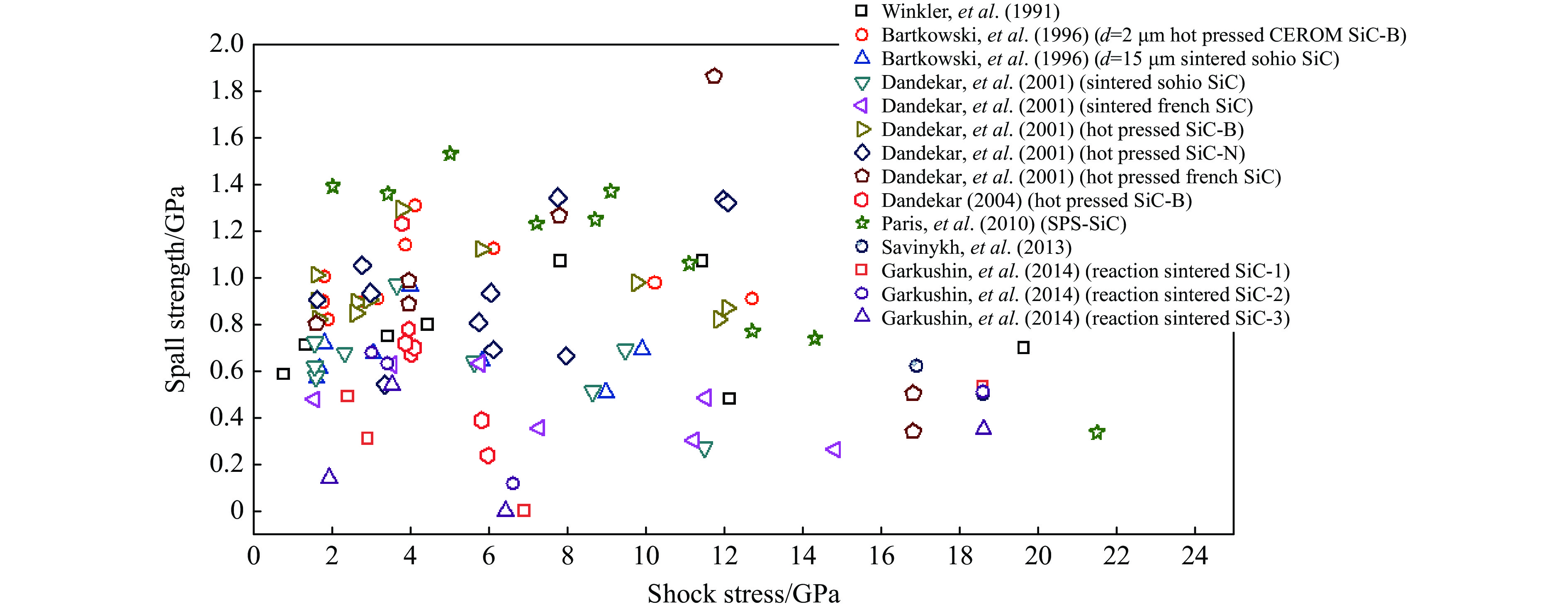
因此,从层裂实验中可以看出,SiC陶瓷的动态抗拉强度差异显著,且强度均相对较低,与制备工艺差异引起的SiC样品纯度、密度和微结构不同密切相关。图11给出了上述研究中的层裂强度与冲击应力的关系。可以看出,SiC的层裂强度受SiC类型、制造工艺以及晶粒尺寸的影响显著。在上述冲击条件下,所有传统的SiC陶瓷的层裂强度均低于2 GPa。尽管如此,对于大多数实验而言,同一种SiC试样的层裂强度随着冲击应力的增加呈先增大后减小的趋势。
1.4 基于激光驱动的脉冲加载实验
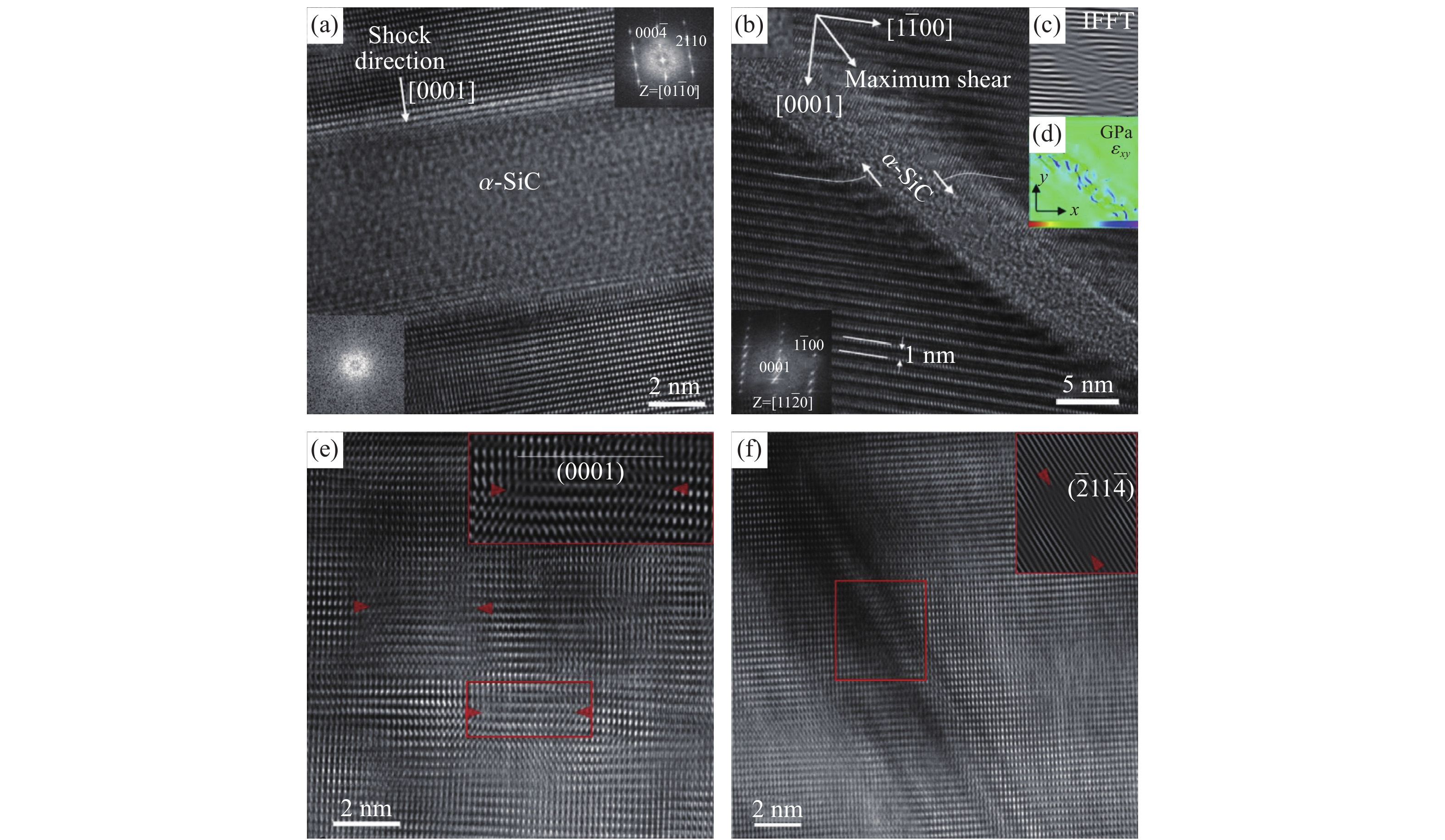
采用近年来发展起来的激光驱动加载技术,激光驱动冲击实验可实现107 s−1以上的超高应变率、纳秒甚至皮秒的超短应力脉冲加载[76-78],已成功应用于脆性固体材料的动态力学行为研究[79-81]。Zhao等[82]通过激光烧蚀驱动,对4H-SiC进行了冲击压缩研究,压力峰值为50 GPa,冲击回收装置如图12所示。激光烧蚀Al片产生高压驱动冲击波进入SiC靶板,采用金属铜腔和动量阻碍区域捕获反射的拉伸应力波,由于金属铜与SiC的阻抗接近,该装置可以减少非必要的拉伸反射,从而保证试件的成块特性。Zhao等[82]详细讨论了冲击引起的局部非晶化,研究表明非晶相是SiC的一种高密度存在形式,增强了其在高压下的热力学稳定性以及冲击压缩中单轴应变状态产生的剪切应力。图13为高分辨率ETM观察到的厚度达5 nm的局部无定形带,这些无定形带或垂直或偏向冲击波传播方向分布。偏向冲击加载方向的无定形带附近的一些晶格发生了偏转,意味着该区域经历了剧烈的剪切变形,相分析进一步证实了这些面内剪切应变的局域化特征。但是,研究发现垂直于冲击的无定形带是意料之外,因为基面上并没有剪切应力,Zhao等[82]猜想这与无定形带的交叉区域有关。除了以上两种无定形带之外,实验中也观察到了层错现象,并认为这是无定形化的前奏。
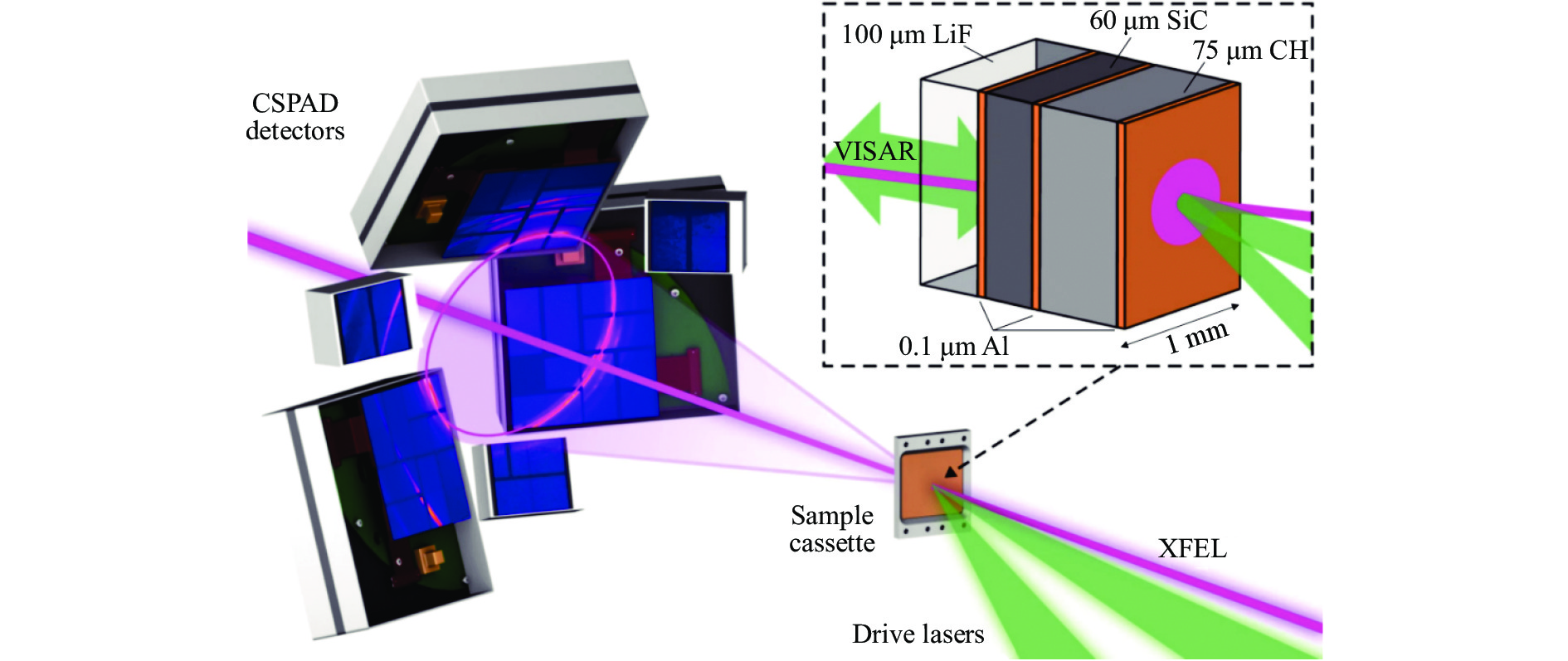
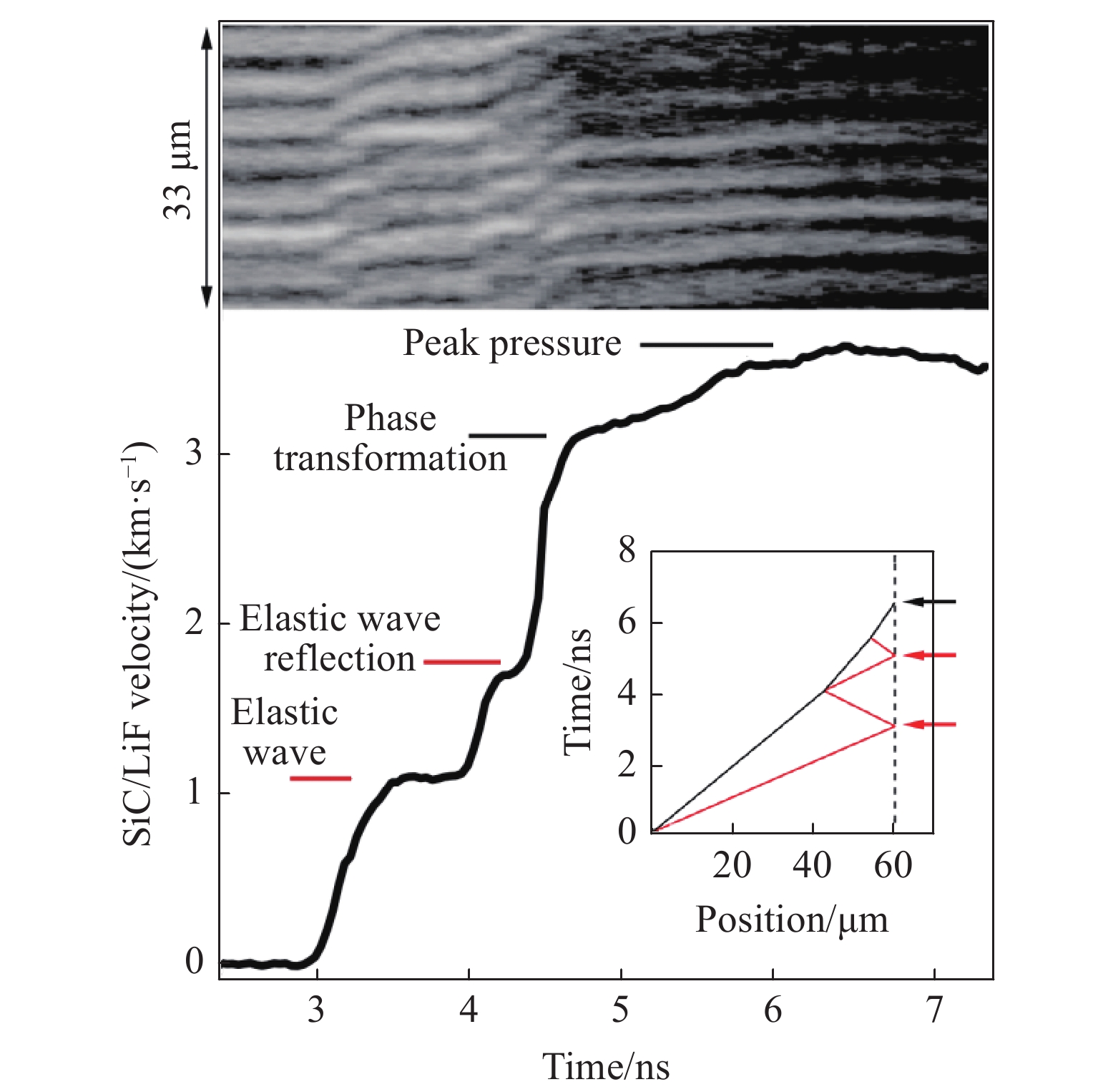
Tracy等[83]利用激光冲击对单晶4H-SiC和多晶3C-SiC进行了冲击相变研究,冲击压力高达206 GPa。实验表明,单晶和多晶SiC从低压四面体相转变为高压岩盐型结构,低压相和高压相在混合相区共存,在200 GPa以上完全转变为岩盐型结构。图14为激光驱动冲击压缩实验装置示意图。样品安装在盒子中,X射线束的入射方向相对于试件法向呈约15°角,两个纳秒激光臂则呈6°和25°角,X射线衍射(XRD)结果记录在CSPAD探测仪中,试件组装包含烧蚀剂、SiC样品和氟化锂窗口,VISAR系统垂直于试样聚焦在试样-窗口界面。图15为VISAR系统记录的典型粒子速度时程曲线。可见,弹性前驱波显著,伴随着相变的界面粒子速度平台发生在约3.1 km/s处,对应的压力约为100 GPa。1.6 km/s处的拐点与反射的弹性波和传播的塑性波相互作用有关。
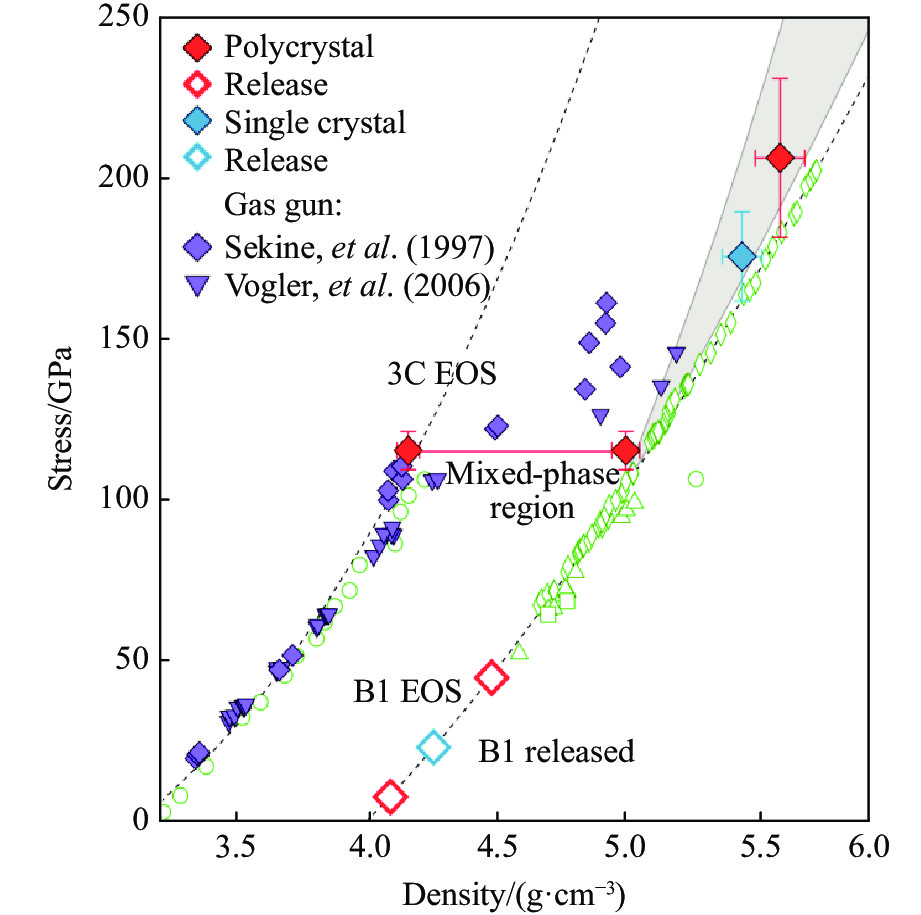
在该激光冲击实验中,通过图15中的弹性波阶段测量的Hugoniot弹性极限在26~29 GPa之间,高于轻气炮实验研究中的11.5~18.9 GPa范围[46, 61, 63, 84]。弹性极限增强是由于高应变率加载引起的,与其他材料的高应变率激光驱动加载实验报道的高弹性极限一致[85-86]。图16是SiC的Hugoniot状态曲线,其中包含一条基于Mie-Grüneisen状态方程计算的岩盐型结构相的理论Hugoniot曲线。该工作中岩盐型结构相的实验值与理论计算值基本一致。对于206和175 GPa的情况,XRD数据获得的岩盐型结构相密度与计算的Hugoniot值较吻合;但是114 GPa下观测到了压缩的3C相和新相B1相共存现象。通过比较卸载下的密度变化发现,岩盐型结构相保持至5 GPa,意味着岩盐型结构相在卸载时体积大幅膨胀。Tracy等在高压冲击实验中观察到了卸载过程中高达38%的岩盐型结构相的体积膨胀,在纳秒时间尺度直接观测到岩盐型结构相的转变,但没有直接的证据证明存在中间相。实验结果预示了任何经过中间相的相变路径应该发生在亚纳秒时间尺度,与第一性原理分子动力学(MD)模拟结果相符合。因此,若在实验层面探测中间结构,需要飞秒时间分辨率的XRD技术。
综上所述,目前关于SiC动态力学行为和性质的研究是多方面、多层次的,包括抗弹性能和动态破碎[37, 87-88],基于霍普金森压杆设备、轻气炮以及激光驱动装置等宽应变率和宽压力范围的材料动力学研究极大地丰富了SiC陶瓷冲击响应的研究内容,从多个研究角度提供了有益参考。同时,也应注意到目前SiC陶瓷的实验研究仍主要基于平面冲击和霍普金森压杆动态实验,其应变率通常在102~106 s−1(大多数低于105 s−1)之间,而近些年激光冲击加载则越来越广泛地应用到材料高应变率行为研究中[19]。
2. SiC动力学行为模拟和高压相变理论计算
随着高性能计算机的快速发展,理论计算和数值模拟已然成为了极其重要的研究方式,与实验研究相辅相成,既对实验前期有重要的指导作用,也对实验后期有重要的补充作用,许多受限于实验诊断技术的现象和机理在计算和模拟中得到解决。SiC材料的理论计算和模拟研究主要包括基于连续介质的模拟和基于原子尺度的模拟。
2.1 基于连续介质的宏观尺度模拟
在冲击载荷下,陶瓷材料的变形和损伤可分为弹性、塑性和微裂纹等。考虑到实验中大多情况下难以对所需的物理参数进行直接无损测量,采用连续介质模拟等计算手段可以在基于良好陶瓷材料本构模型的情况下,对陶瓷材料中各种可能的变形和破坏模式进行探讨。这类方法的突出优点是模拟材料样本可以是真实的宏观尺度,可以直接与常规实验进行比较,缺点是本构模型中的许多参数为经验值,适用范围有限,导致其可预测性一直受到质疑,此外,模型在准确描述裂纹扩展方面仍然存在不足[89]。另一方面,连续介质模拟强烈依赖于包含多参数的材料本构方程,而这些参数又与实验数据相关,因此该方法难以确保参数的独立性。对于采用不同工艺制备的实验样品,其实验参数也可能随之改变。目前的陶瓷材料本构模型大多是唯象的,尚无法反映SiC材料在高压下的塑性变形和结构相变等重要的材料性质。
2.1.1 陶瓷类材料的本构模型和状态方程
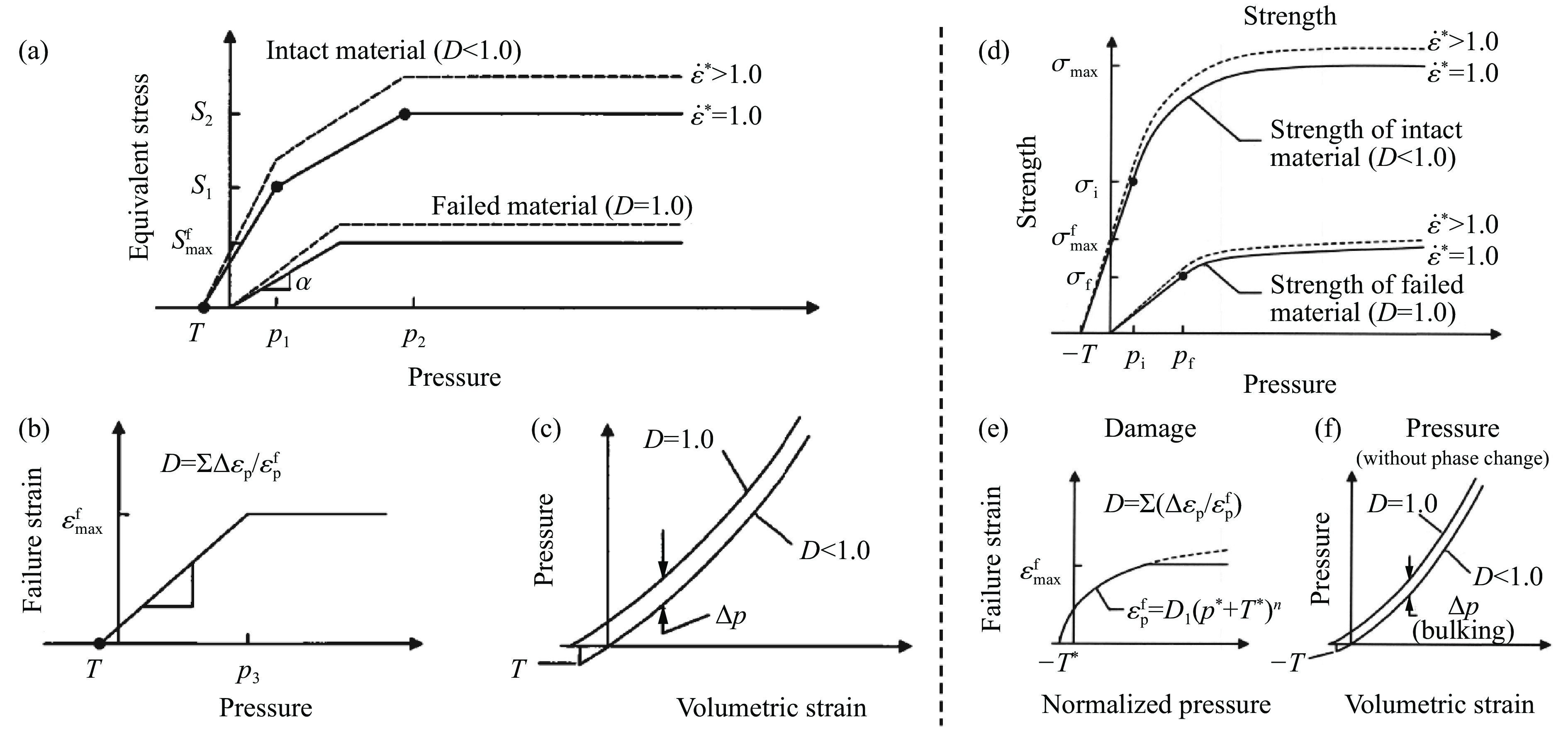
陶瓷材料动态力学行为数值模拟的准确性很大程度上取决于动态本构模型和状态方程,目前已提出了多种状态方程和本构模型[90-98]。例如,Fahrenthold[90]提出了带损伤的动态本构模型,以研究氧化铝陶瓷的侵彻问题,其中用Weibull分布描述微裂纹等缺陷尺寸对损伤率的影响。在Rajendran等[99]的研究模型中,材料强度是率相关的,基于弹塑性开裂准则,模拟了AD85陶瓷的非弹性变形。任会兰等[100]运用细观损伤力学理论,从陶瓷材料内翼型裂纹的产生和扩展损伤机理出发,忽略不同荷载下损伤机制的差异,建立了陶瓷材料的弹脆性动态损伤本构模型,成功用于冲击载荷下AD90陶瓷的动态应力-应变曲线计算,模拟结果与实验相符。目前,使用最广泛的陶瓷材料本构模型仍然是Johnson-Holmquist(JH)模型,如图17所示,包括JH-1、JH-2和JH-B(Johnson-Holmquist-Beissel)等具体形式[101-102]。其中,S1和S2为完整材料强度,
Sfmax 为最大失效强度,D为损伤因子。JH-2模型是在JH-1的基础上发展起来的,它基于两个压力相关的屈服面,分别为无缺陷和失效后的材料强度。最近,唐瑞涛等[103]提出了基于多项式形式的状态方程,其强度模型考虑了压力硬化、应变率、剪切损伤和拉伸软化等各种效应。更多有关陶瓷的动态损伤本构模型可参考Rajendran等[99]、Anderson等[104]及Walley[105](装甲应用相关的陶瓷冲击特性历史与相关模型研究)的综述。2.1.2 SiC等陶瓷类材料的连续介质模拟
在连续介质模拟研究中,Rajendran等[99]基于实验或理论分析提出了本构模型,研究了SiC等陶瓷材料的冲击和高应变率行为,基于实验对陶瓷模型参数进行了系统评估。该模型在很大程度上再现了平板冲击实验中的粒子速度剖面,计算得到的应力-应变曲线显示SiC的HEL约为18 GPa,大于参照实验的15 GPa,他们将其解释为受连续介质模型中应变率依赖关系的影响。Holmquist等[101]的一系列连续介质模拟研究是具有代表性的工作之一。他们使用JH-1本构模型分析了SiC的高速冲击响应,并模拟了各种冲击问题,如平板冲击、抗侵彻测试等,计算结果与参照实验较为吻合。随后Holmquist等[102]在后续工作中基于更准确的JH-B脆性材料本构模型,对SiC的高速冲击响应进行了模拟研究,如图18所示,其中:L为弹体长度,D为直径。Anderson[104]则对包含SiC在内的陶瓷材料装甲计算模型进行了综述。
Zhu[106]利用平板冲击实验数据研究了多晶氧化铝陶瓷在冲击压缩下的非弹性变形和有效强度。该模型分为两步:第1步与动态有限元分析类似,通过将波剖面速度与实验测量数据相匹配,验证或优化宏观均匀材料模型参数;第2步采用Voronoi多晶方法,从介观尺度分析验证或优化多晶材料的模型参数。Levy等[107]使用黏结域模型的有限元方法,研究了陶瓷的动态碎裂。易洪昇等[108]通过霍普金森压杆开展了动态单轴压缩试验和有限元模拟,研究了不同加载速度下脆性颗粒的破坏特性,按照加载速度的不同,将材料破坏分为拉伸破坏、过度破坏以及剪切破坏。易荣成等[109]则以复合陶瓷为弹体,利用有限元建模,模拟了陶瓷易碎弹对铝板的冲击。在陶瓷的冲击损伤过程中,裂纹扩展会导致场变量不连续,由于计算域的连续要求,基于网格的有限元法在许多材料分离的场景下应用有限。Chakraborty等[110]则采用基于粒子的光滑粒子流体动力学(SPH)计算框架作为一种替代方法,基于JH-1的本构模型,用改进后的SPH方法对脆性陶瓷的损伤演化进行了模拟。Cooper等[111]则使用推导的本构模型进行预测,结果发现,冲击压力低于HEL时的层裂强度降低是由速率相关的损伤演变引起的,这种演变与非弹性变形和多孔扩张的有效速率相关联,其计算的层裂强度与之前的实验非常一致。最近,Merzhievskii[112]对强动态荷载下的变形模型进行了综述,包括连续介质模型、微观结构模型和原子分子动力学模型。Chi等[113]模拟了长杆弹丸撞击预应力约束的陶瓷靶,通过比较弹道性能结果,验证了模型的有效性,由此对具有不同预应力条件(径向应力、轴向应力、静水压力、无预应力)的受限陶瓷进行了冲击模拟,探讨了其对陶瓷弹道性能的影响。Tang等[114]也使用解析模型研究了陶瓷的弹丸冲击行为,他们假设弹丸在冲击过程中的动能通过弹丸变形和侵蚀、压缩碎裂和剪切失效而耗散,计算结果与实验结果比较接近。Zhang等[115]采用JH-2模型模拟了SHPB实验,并根据实验结果进行了参数标定,基于非线性应力-应变响应的发展和位错演化,得出6H-SiC在高加载速率下可以发生塑性变形的结论。
2.2 基于原子模拟的微纳观尺度模拟
基于MD方法的原子模拟在材料的物理力学性能研究中应用广泛,特别是高温高压以及高应变率等极端条件下的材料行为。原子模拟可以直接提供原子尺度的变形细节,从而有助于理解损伤的起始和演变过程。与实验研究相比,原子模拟方法可以直接获得多个关键物理量。数百万至数十亿原子的大规模MD模拟已经获得越来越多的应用[116-119]。原子间的相互作用势通常是基于第一性原理计算或半经验的函数模型,其参数具有较明确的物理含义,可较好地再现材料在平衡态的关键性质特征。基于可靠的原子间势能函数,通过MD模拟,可以对材料的动力学过程进行由表及里的全方位、全时段观测。尽管对陶瓷类材料在微纳米尺度的研究需求很大,但目前基于MD模拟对陶瓷类材料的研究体量远小于金属材料,其重要原因之一是适用于陶瓷材料大变形研究的原子间相互作用势发展滞后。
2.2.1 SiC原子间相互作用势能
MD模拟中,原子之间的相互作用体现在对应的势函数中。材料或结构的物理力学行为从根本上取决于势函数的形式和相关参数,而这些参数通常可以从量子力学计算中获得,也可以通过实验的方法得到。从某种意义上说,势函数就是微纳米层面原子分子体系中的“本构方程”。目前,有关SiC材料的原子间相互作用势主要包括Tersoff势函数[120-123]和Vashishta势函数[124]。经典的Tersoff势表示为[120]
{E=∑iEi=12∑i≠jVijVij=fC(rij)[fR(rij)+bijfA(rij)]fR(rij)=Aijexp(−λijrij)fA(rij)=Bijexp(−μijrij) (1) 式中:E为系统能量;
Vij 为两体势;fC 、fA 、fR 分别为截断能电势、吸引对电势和排斥对电势;rij 为原子i到原子j的距离;bij 为键阶的一个度量,现假设为原子i和原子j配位的单调递减函数;Aij 、Bij 、λij 和μij 仅依赖于原子类型[120]。Erhart-Albe对Tersoff势函数进行了修正,黏结能量为各键能之和E=∑i>jfC(rij)[pR(rij)−bij+bji2pA(rij)] (2) 式中:
p R为排斥力,pA 为吸引力。成对的牵引力和排斥力分别为pR(r)=D0S−1exp[−γ√2S(r−r0)] (3) pA(r)=SD0S−1exp[−γ√2/S(r−r0)] (4) 式中:r为原子间距离,D0和r0分别为二聚体的能量和键长,γ根据二聚体的基态振荡频率确定,S为鲍林图的斜率。
Vashishta势函数则考虑了库伦屏蔽(Screened Coulomb)、电荷偶极子(Charge-dipole)、范德华(van der Waals)、空间排斥(Steric repulsion)以及三体相互作用(Three-body interactions)等多个效应。该势函数包含了二体和三体项
E=∑i<jV(2)ij(rij)+∑i;j<kV(3)jik(rij,rik,cosθjik) (5) 式中:
V(2)ij(rij) 为二体项;V(3)jik(rij,rik,cosθjik) 为三体项;rij=|rij| ,rij=ri−rj ;cosθjik=rij⋅rik/rijrik 。二体项具体形式为V(2)ij(r)=Hijrηij+keZiZjre−r/λ−keDij2r4e−r/ξ−Wijr6 (6) 式中:
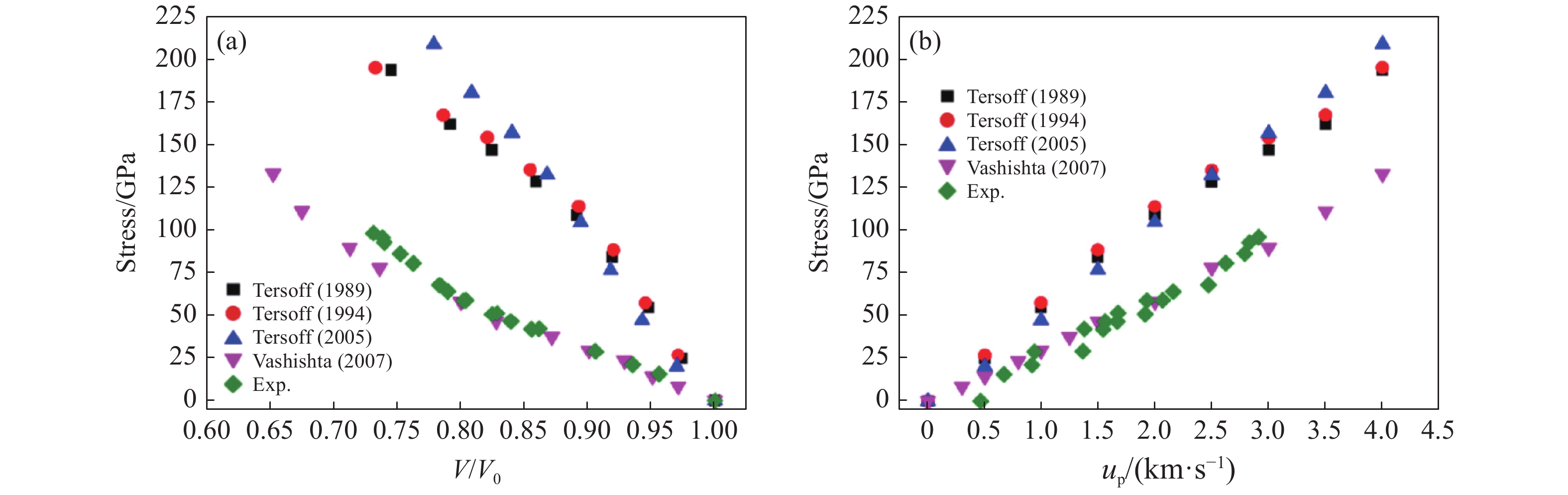
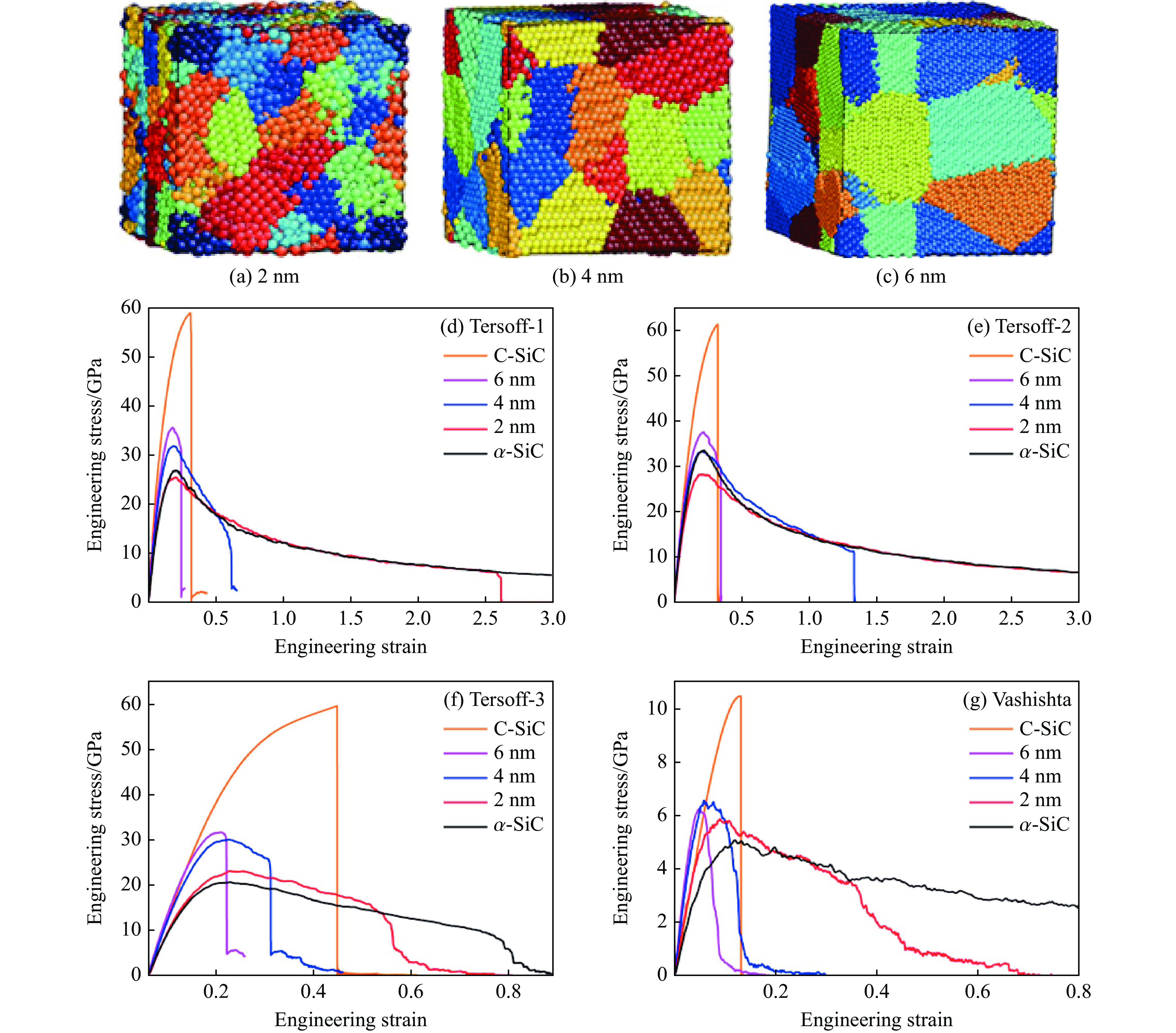
Hij 为排斥力强度,Zi 、Zj 为有效电荷,Dij 为电荷偶吸引力强度,Wij 为范德华力强度,ηij 为排斥力项指数,ke 为库伦常数,λ 和ξ 分别为库仑和电荷偶项系数。利用MD方法开展材料或结构的物理力学行为研究之前,需要对势函数的合理性、适用性、准确性进行分析和验证。只有建立在可靠的势能函数基础上,MD计算模拟的结果才有意义和价值。据此,Li等[125]分别对Tersoff (1989)[120]、Tersoff (1994)[122]、Erhart等 (2005)[123]和Vashishta(2007)[124]等4种具体的原子间相互作用势进行了分析比较,通过超大规模MD模拟研究了这些势函数在SiC平面中的冲击问题。如图19所示,该工作证明了Vashishta势函数是目前描述冲击载荷下SiC陶瓷最合适的势函数。该势函数已被成功应用于多种陶瓷材料的冲击响应研究,包括AlN[126-128]、Al2O3[129-132]和SiC[133-137]等。对SiC而言,该势函数的最大优势是能够准确反映3C-SiC在高压下的结构相变[124, 138],并能够准确预测与实验测量值高度一致的陶瓷材料熔点[124]。与传统的Tersoff势函数[120-123]相比,Vashishta势函数适用于SiC陶瓷材料的冲击响应模拟[125],模拟所得的Hugoniot曲线与实验数据非常接近。
2.2.2 SiC等陶瓷类材料动力学问题的原子模拟
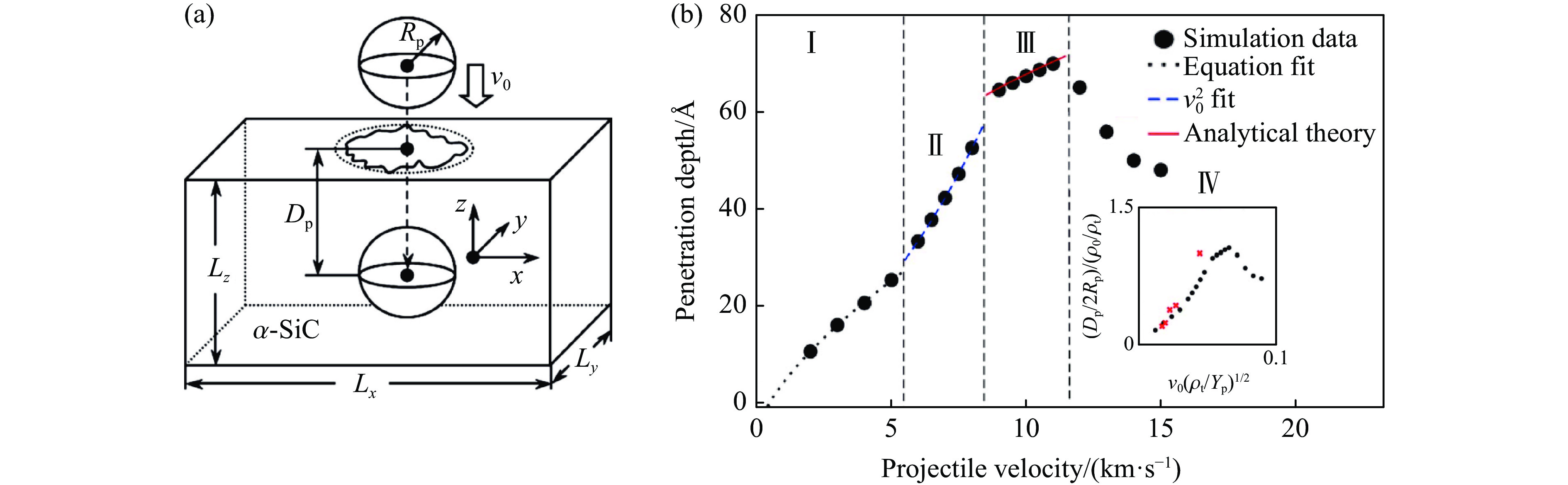
Makeev等[139]则通过基于Tersoff势的MD模拟,研究了在金刚石弹丸的高超声速冲击下非晶SiC靶的动态损伤响应,如图20所示。研究结果表明,在侵彻深度中发现了4种不同的损伤状态:浅坑形成、深入靶板、深度穿透与靶板的局部熔化以及入射弹体完全崩解。Makeev等[140-141]也通过模拟比较了非晶SiC及其碳纳米管增强材料在冲击载荷下的响应,如图21所示。Branicio等[133]模拟研究了刚性弹丸以15 km/s超高速碰撞SiC靶板的情况,其模型包含3亿个原子,是迄今为止最大规模的SiC陶瓷材料MD模拟,如图22所示。研究结果表明,撞击时产生的巨大压力和温度梯度会引起局部熔化甚至汽化,并产生强烈的冲击波,冲击峰值应力达150 GPa,冲击波速度最高可达24 km/s。当冲击压力达到89 GPa以上时,可观察到SiC中从闪锌矿结构到盐岩结构的相变。该模拟揭示了由单个位错核心参与的纳米延性诱导的裂纹成核机制,如图23所示。原子损伤机制涉及从冲击引起的结构转变到塑性变形再到脆性断裂的动态转变。压缩过程中剪切应力高达45 GPa,压缩冲击波在自由表面反射后,局部拉应力可达20 GPa。Zhang等[134]采用MD方法初步研究了SiC的Hugoniot性质,发现SiC中冲击引起的塑性变形主要以变形孪晶的形式存在。他们还采用平面冲击方法研究了具有不同晶体取向的单晶SiC和晶粒尺寸分别为5 nm和10 nm的纳米晶体样品[135-136],获得的Hugoniot数据和压缩强度与实验吻合较好。
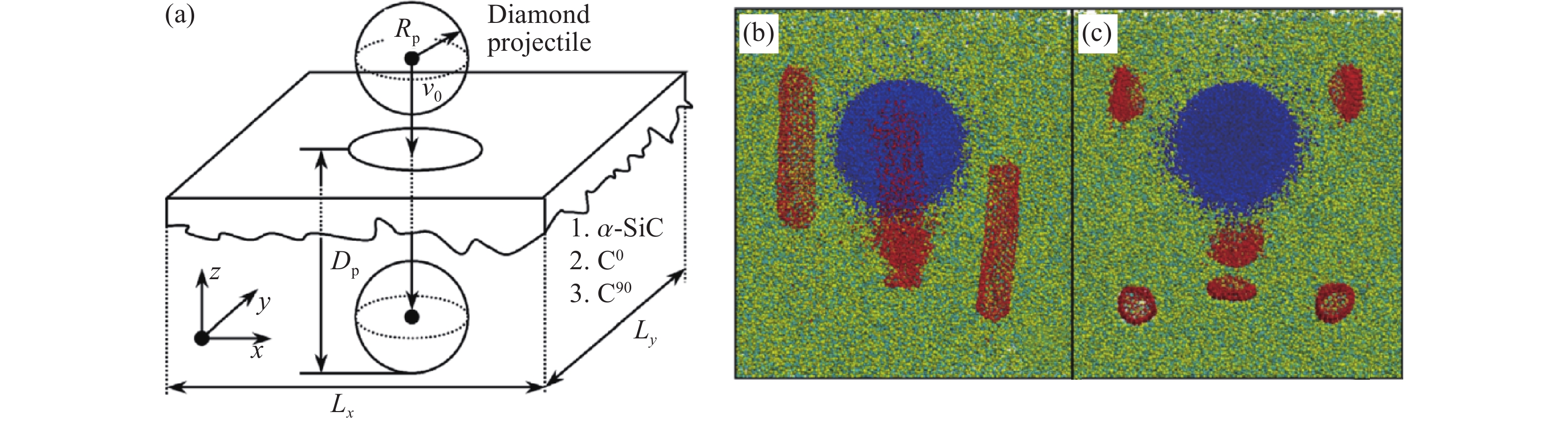
 图 21 金刚石弹丸撞击原始无定形SiC和CNT/无定形SiC复合靶示意图: (a) 半径为2.5 nm的球形金刚石弹丸沿z轴反方向冲击目标,(b)~(c) 由弹丸冲击而造成的碳纳米管损伤[140]Figure 21. Schematic diagram of diamond projectile impacting original amorphous SiC and CNT/amorphous SiC composite targets: (a) diamond projectile with a radius of 2.5 nm impacting on target along negative z axis; (b)–(c) projectile impact induced damage of CNT[140]
图 21 金刚石弹丸撞击原始无定形SiC和CNT/无定形SiC复合靶示意图: (a) 半径为2.5 nm的球形金刚石弹丸沿z轴反方向冲击目标,(b)~(c) 由弹丸冲击而造成的碳纳米管损伤[140]Figure 21. Schematic diagram of diamond projectile impacting original amorphous SiC and CNT/amorphous SiC composite targets: (a) diamond projectile with a radius of 2.5 nm impacting on target along negative z axis; (b)–(c) projectile impact induced damage of CNT[140] 图 23 冲击碳化硅中位错、脆性裂纹引起的形核和生长: (a) 13.05 ps时位错线上形成的脆性裂纹(白色箭头处); (b) 闪锌晶型在{110}平面形成的裂纹扩展; (c) 27 ps 时材料裂纹扩展; (d) 31.2 ps时材料后表面开裂[133]Figure 23. Nucleation and growth of brittle cracks from dislocations in shocked SiC: (a) white arrows indicate brittle cracks nucleating directly from dislocation lines at 13.05 ps; (b) cracks cleaving {110} planes of the zinc blende crystal in the direction of the back surface; (c) cracked configuration at 27 ps; (d) cracked back surface at 31.2 ps[133]
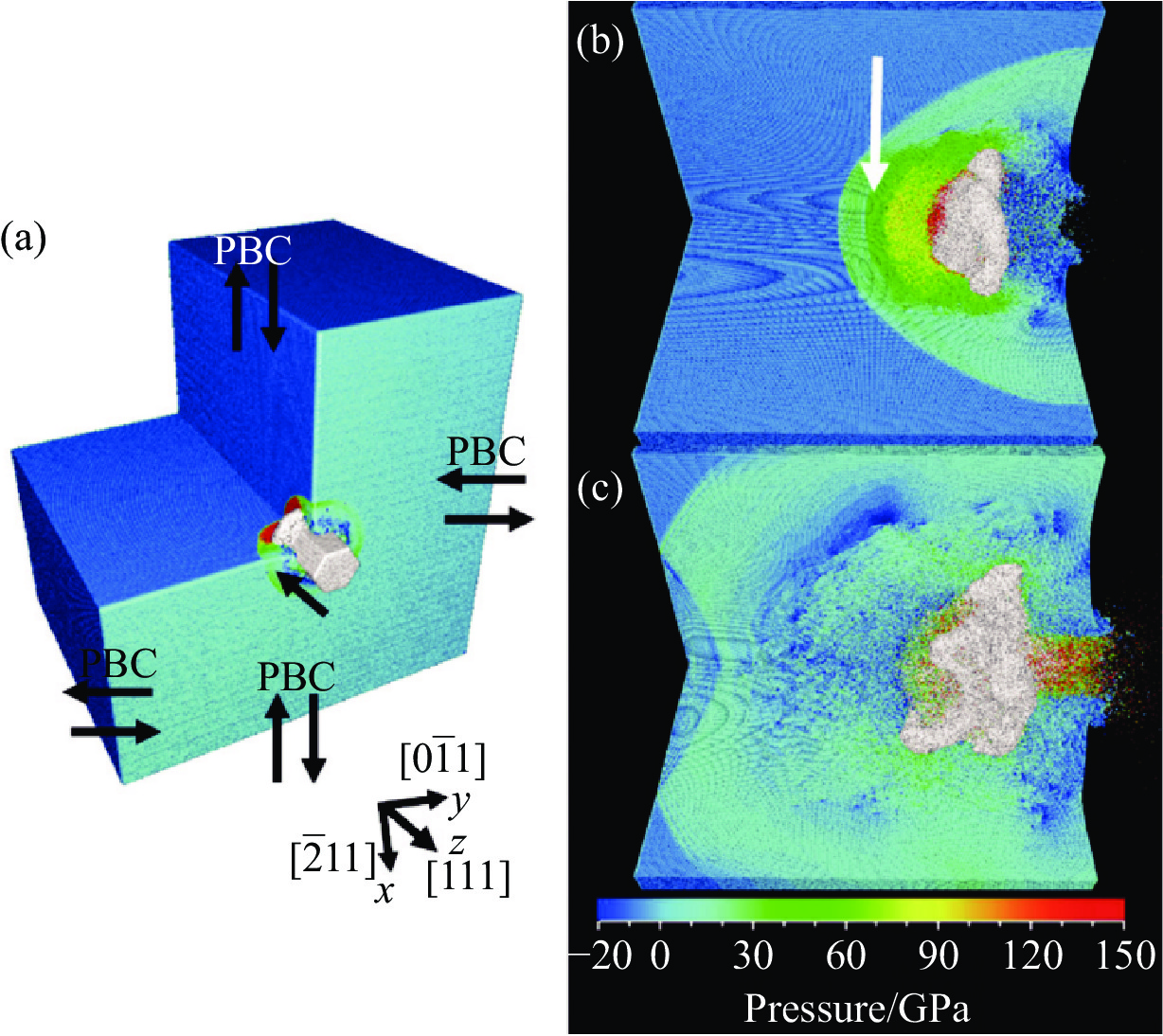
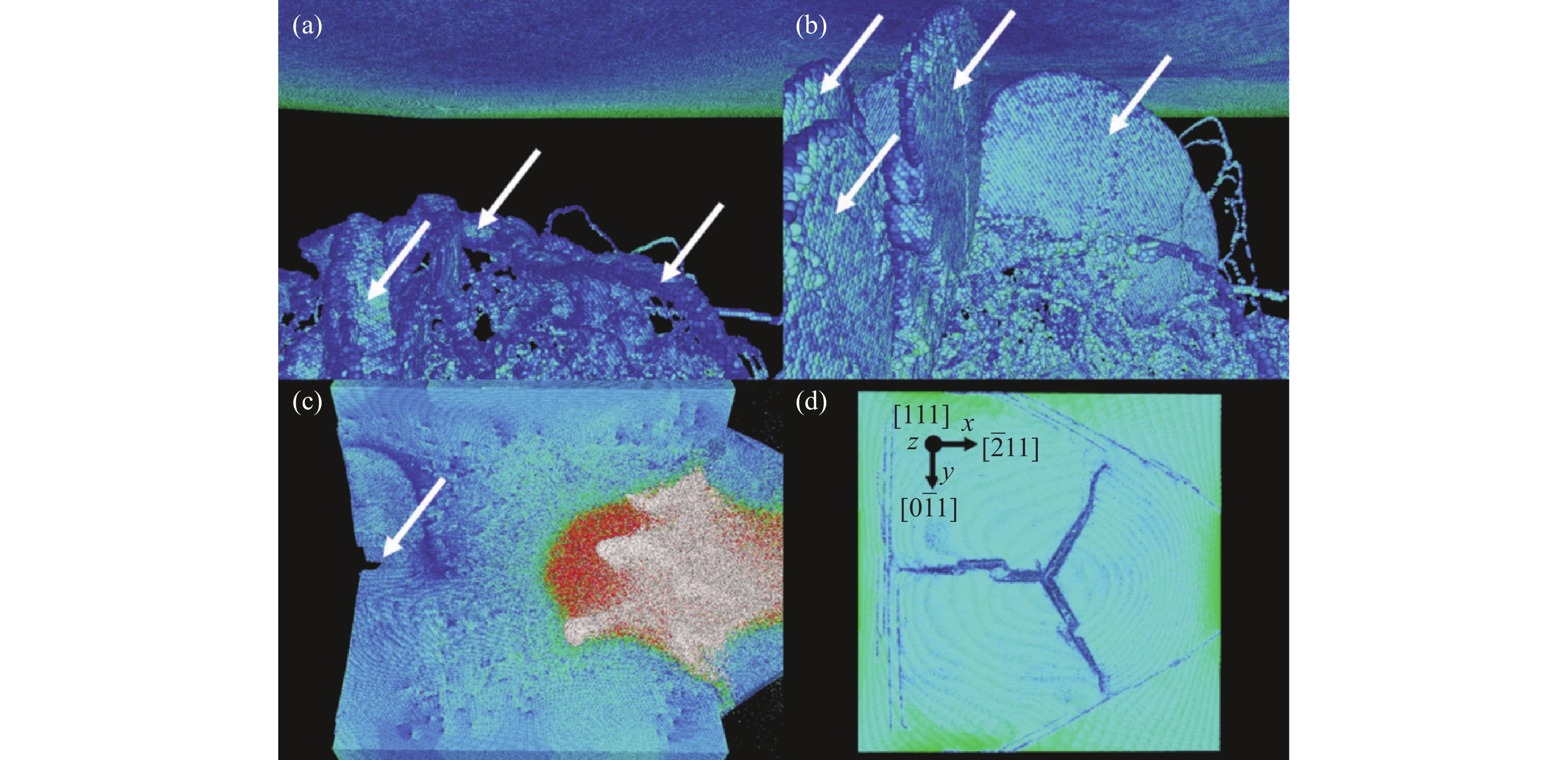
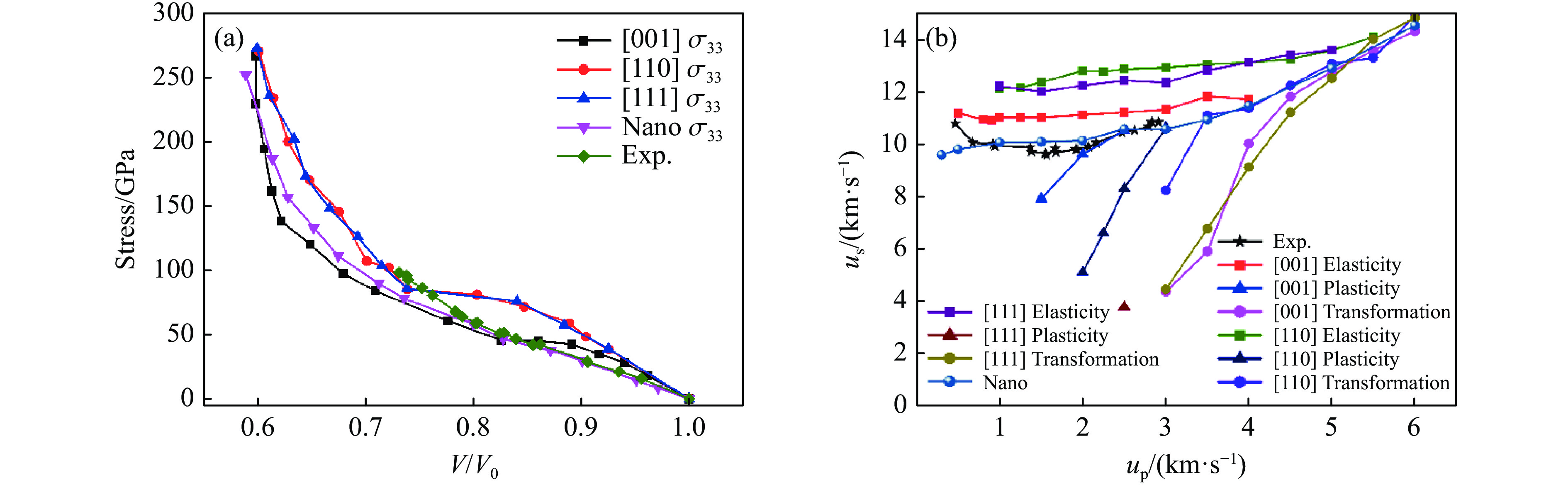
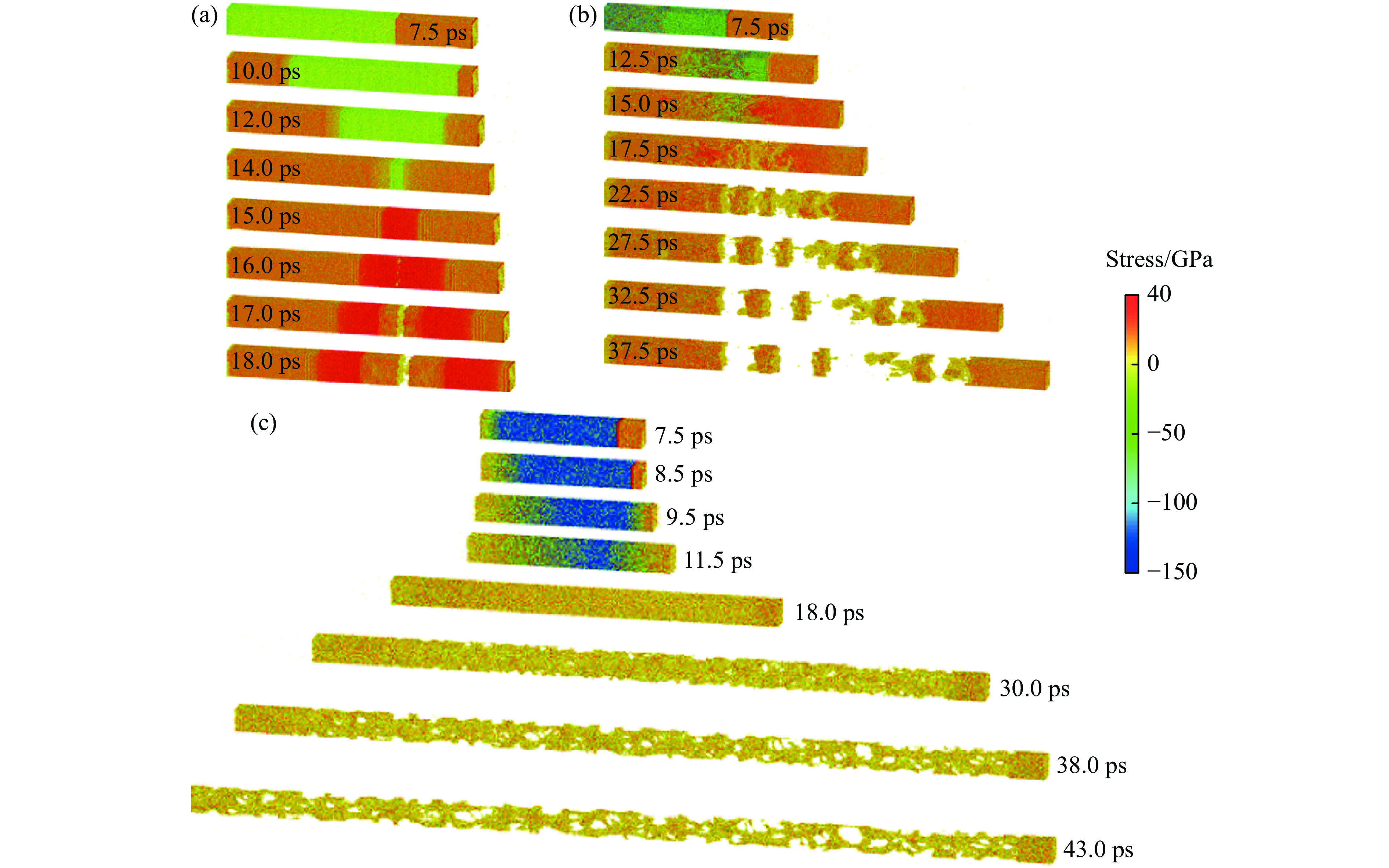
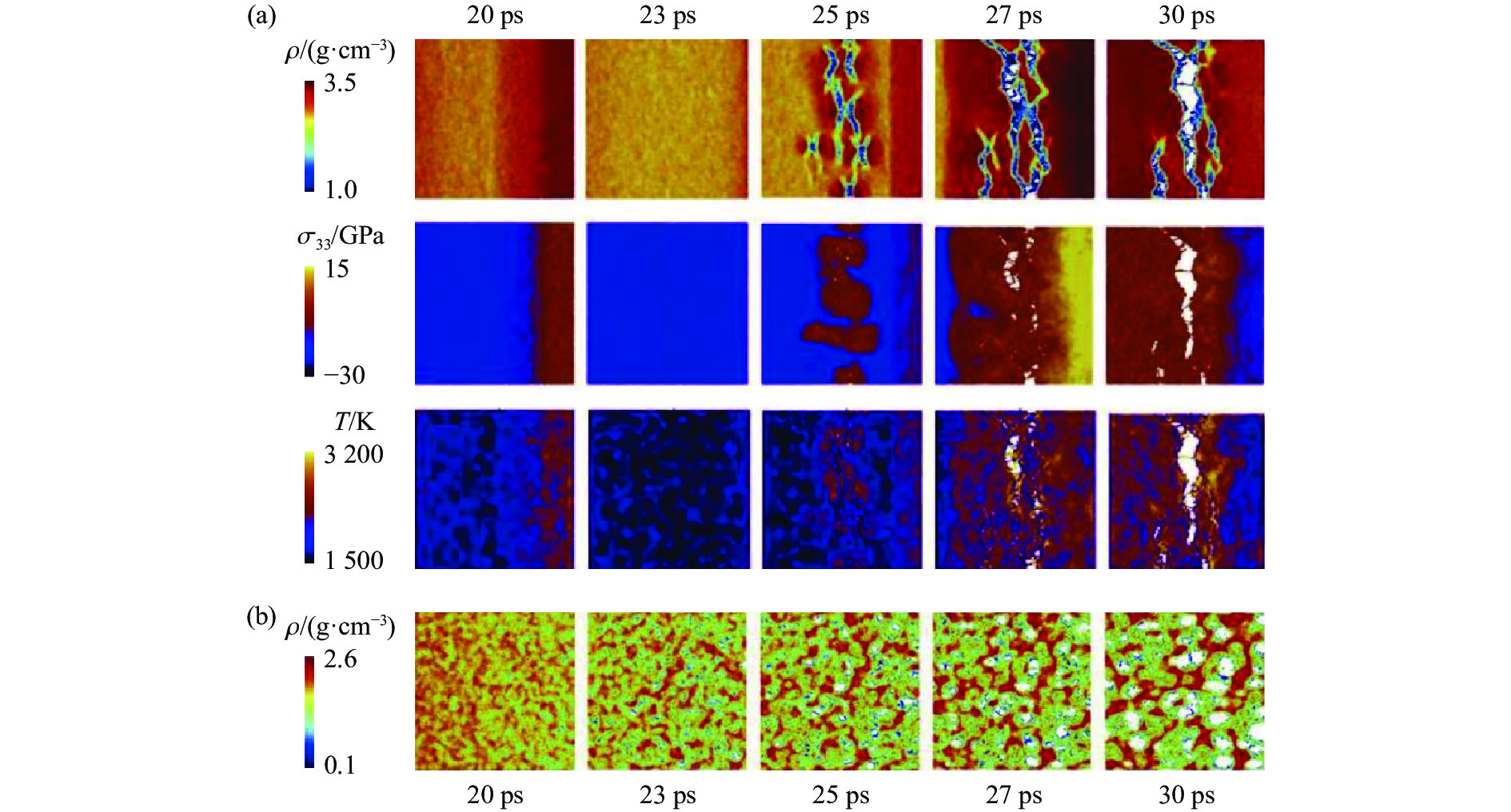
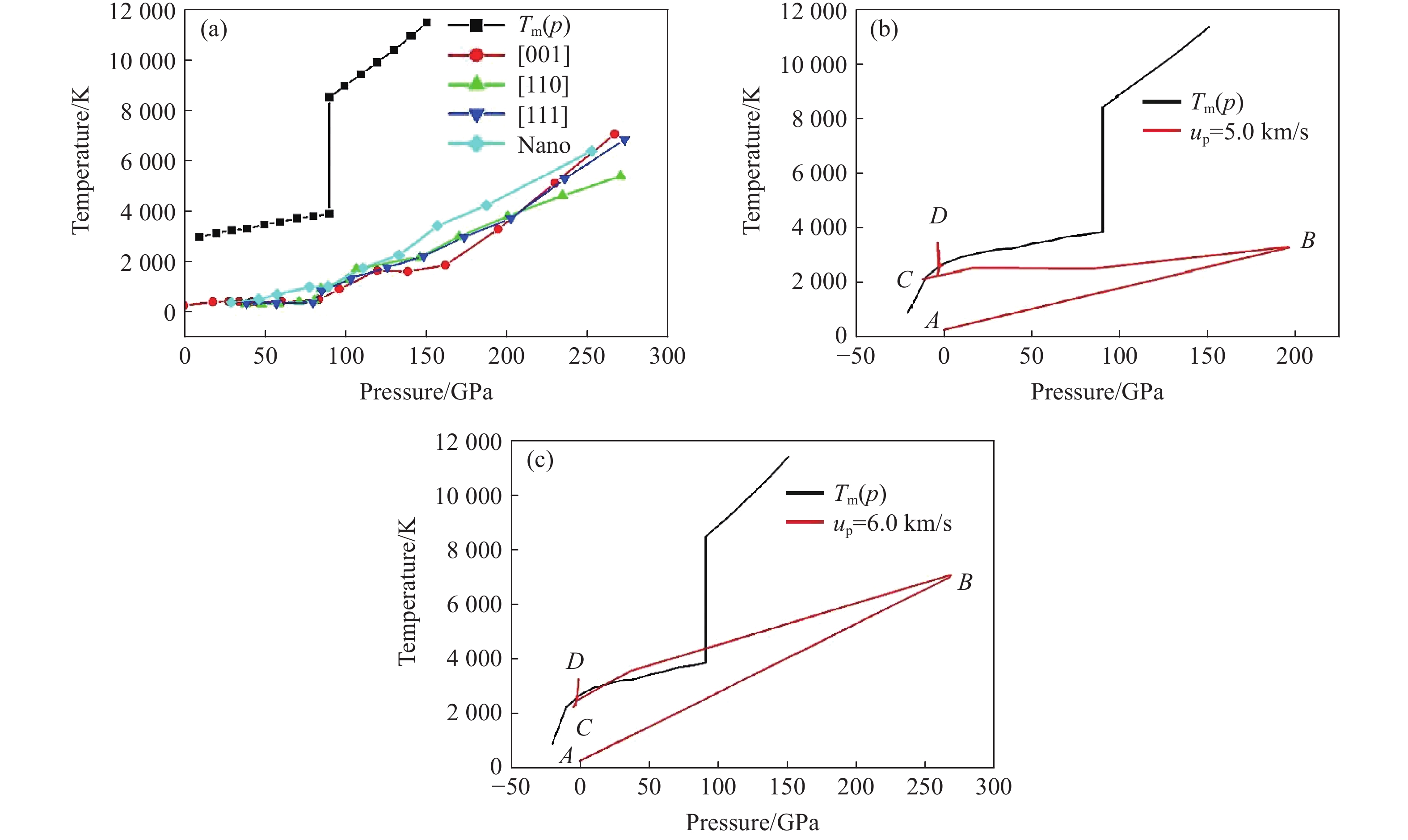
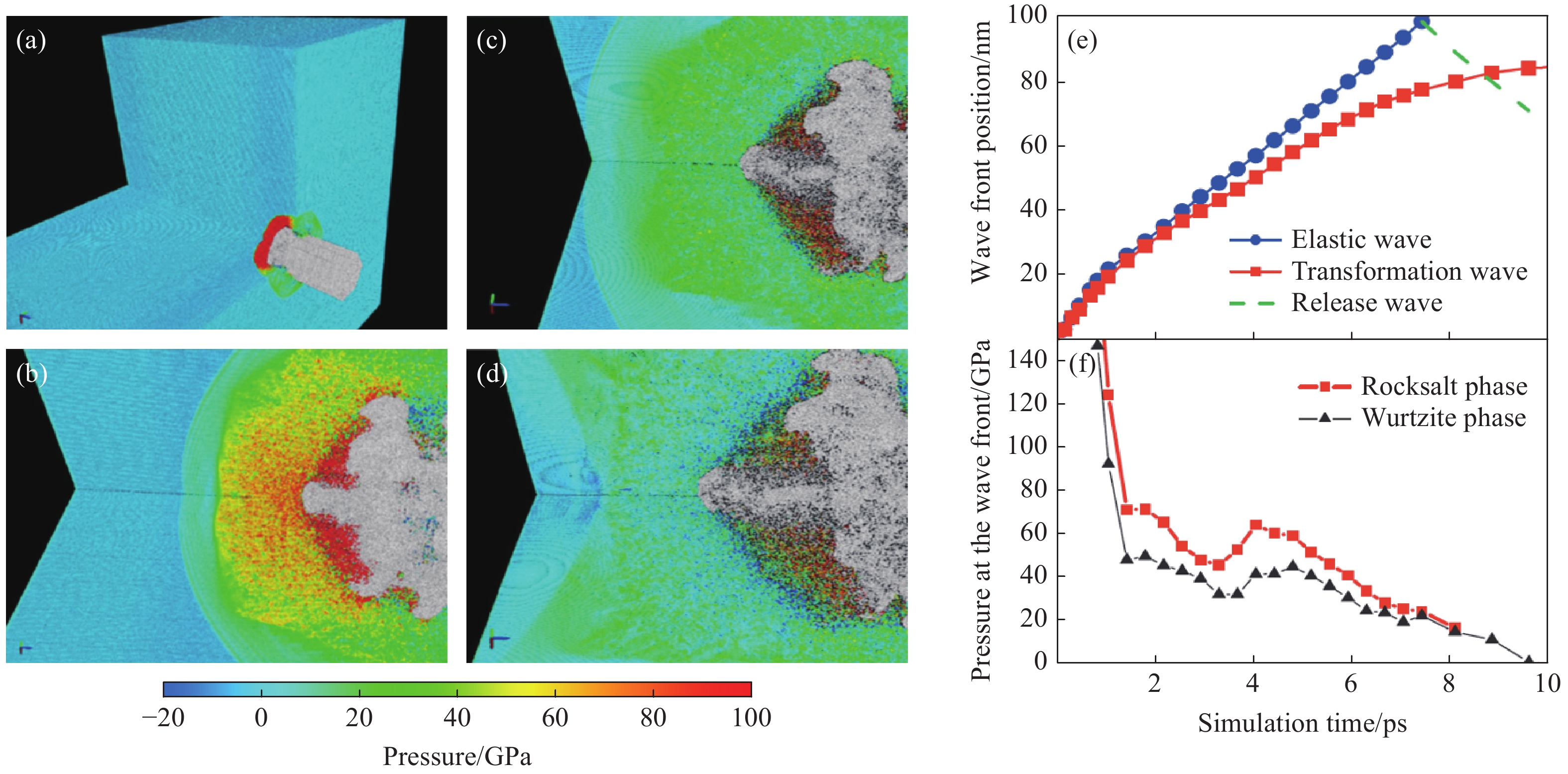
图 23 冲击碳化硅中位错、脆性裂纹引起的形核和生长: (a) 13.05 ps时位错线上形成的脆性裂纹(白色箭头处); (b) 闪锌晶型在{110}平面形成的裂纹扩展; (c) 27 ps 时材料裂纹扩展; (d) 31.2 ps时材料后表面开裂[133]Figure 23. Nucleation and growth of brittle cracks from dislocations in shocked SiC: (a) white arrows indicate brittle cracks nucleating directly from dislocation lines at 13.05 ps; (b) cracks cleaving {110} planes of the zinc blende crystal in the direction of the back surface; (c) cracked configuration at 27 ps; (d) cracked back surface at 31.2 ps[133]Li等[137, 142-144]基于大规模MD方法系统深入地研究了SiC陶瓷材料在极端条件下的变形、损伤和破坏行为,详细分析了其中的动力学过程和涉及的微观机理。在其系列研究工作中,主要针对SiC单晶和纳米多晶体的冲击塑性、相变和层裂破环行为进行研究,揭示了冲击压力、初始环境温度、纳米晶粒尺寸等因素对材料动力学特性和行为的影响。图24显示了常温条件下不同晶向SiC单晶和纳米多晶体的冲击压力-体积和波速-粒子速度Hugoniot曲线[137]。可以看出,该计算模拟得到的Hugoniot状态与实验值吻合较好,且反映了不同晶向对Hugoniot曲线的影响,呈现各向异性。[110]与[111]的Hugoniot压力、弹性波速以及Hugoniot弹性极限比较相似,均高于[001]晶向。此外,各向异性也体现在不同晶向加载时层裂强度的差异。Hugoniot曲线的变化也反映出随着冲击强度增加,SiC的冲击压缩从弹性变形转向塑性变形和结构相变,伴随着弹性波向塑性波及相变波的转变,从单一弹性波向多波结构以及单一强冲击相变波的演化。变形孪晶是此条件下立方晶体SiC的主要塑性机制。冲击层裂逐渐从经典层裂模式转变为微层裂机制,如图25、图26所示。经典层裂表现为局部有限的裂纹萌生、扩展和层裂次数,而微层裂则在几乎整个材料内部发生许多孔洞形核、扩展至贯通进而引起材料崩溃。如图27所示,通过热力学角度,对该现象的演化进行分析,认为由于SiC的熔点极高且随着压力升高而急剧增加,通常情况下SiC在压缩阶段不会熔化,但是在冲击强度极大的情况下SiC会产生大幅温升,卸载过程中可引起局部熔化,从而诱发许多孔洞形核点,引起材料内部大范围失效。
通过改变材料的初始环境温度,研究了初始高温对高熔点SiC材料动力学性能的影响[142]。初始高温对SiC冲击响应的影响主要表现为降低了弹性波速和Hugoniot应力,抑制了变形孪晶的形成,降低了结构相变压力和材料的层裂强度等,得到的高温对结构相变阈值的降低作用与Daviau等[145]开展的高温下SiC的高压相变实验研究结果相符。此外,李旺辉[146]还提出了“准等熵加载”方法,近似等效地研究了材料的“层裂/断裂”行为,详细研究了拉伸应变率在107~1012 s−1范围内SiC材料的抗拉破坏行为,指出在准等熵压缩下单晶SiC的塑性、损伤以及拉伸断裂具有各向异性,并对比分析了不同初始压应变对后续准等熵拉伸断裂行为的影响。单晶SiC的抗拉强度具有各向异性,表现为不同晶向的抗拉强度不同,且在低于1010 s−1时表现为几乎与应变率无关。纳米多晶体的抗拉强度则显示了明显的应变率相关性,尤其在高于1010 s−1时抗拉强度显著增大,接近单晶体的强度值,而低于该应变率时,应变率敏感性降低。值得注意的是,这里所提的应变率敏感性有所降低是相对于1010 s−1以上高度应变率敏感性而言的。实际上在其研究的高应变率范围内,仍然存在应变率效应,即抗拉强度随着应变率的增加而增大。该研究进一步揭示了初始压缩变形对材料拉伸断裂破坏的显著影响,指出不可逆的压缩损伤是材料动态抗拉强度降低的关键因素。
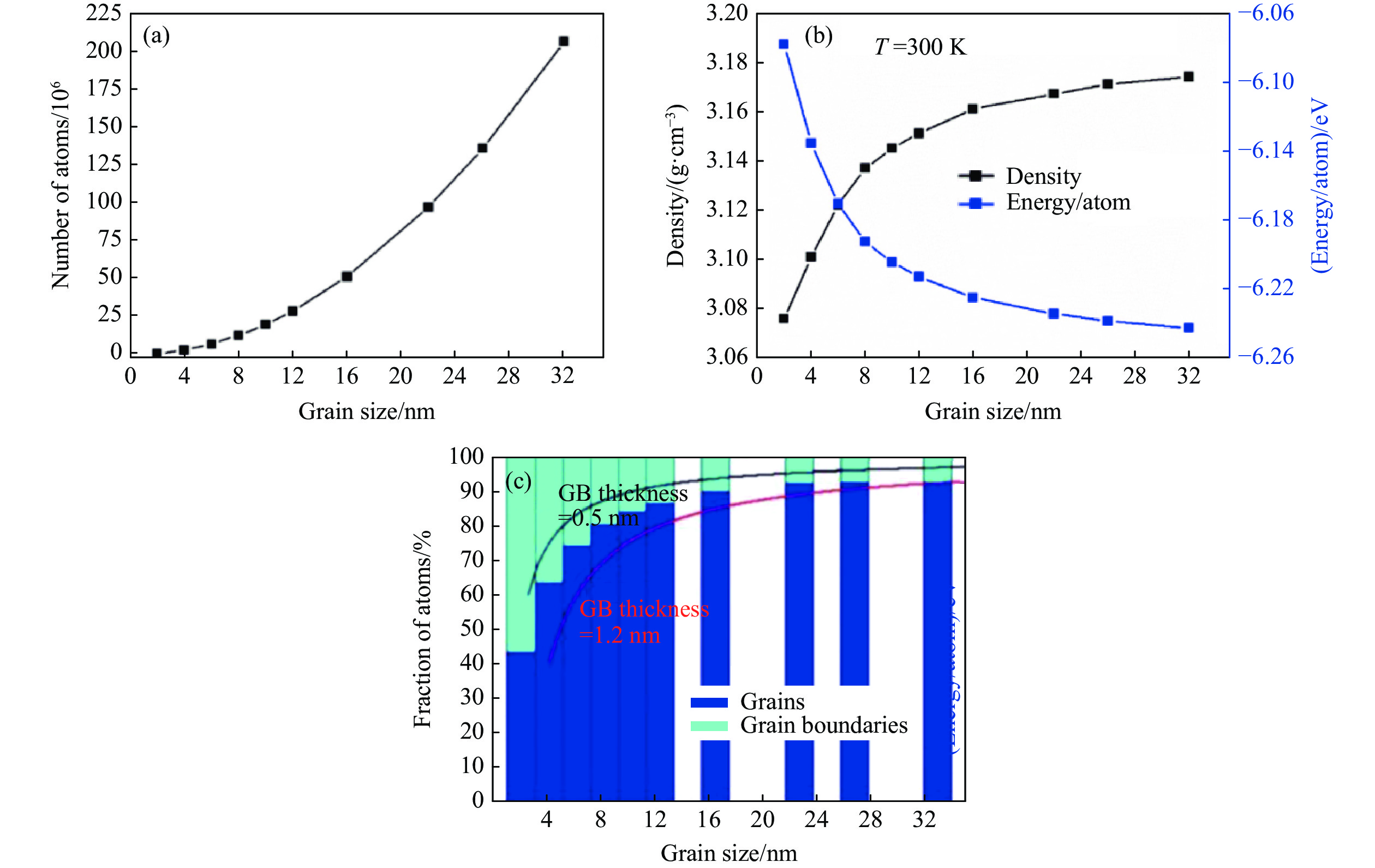
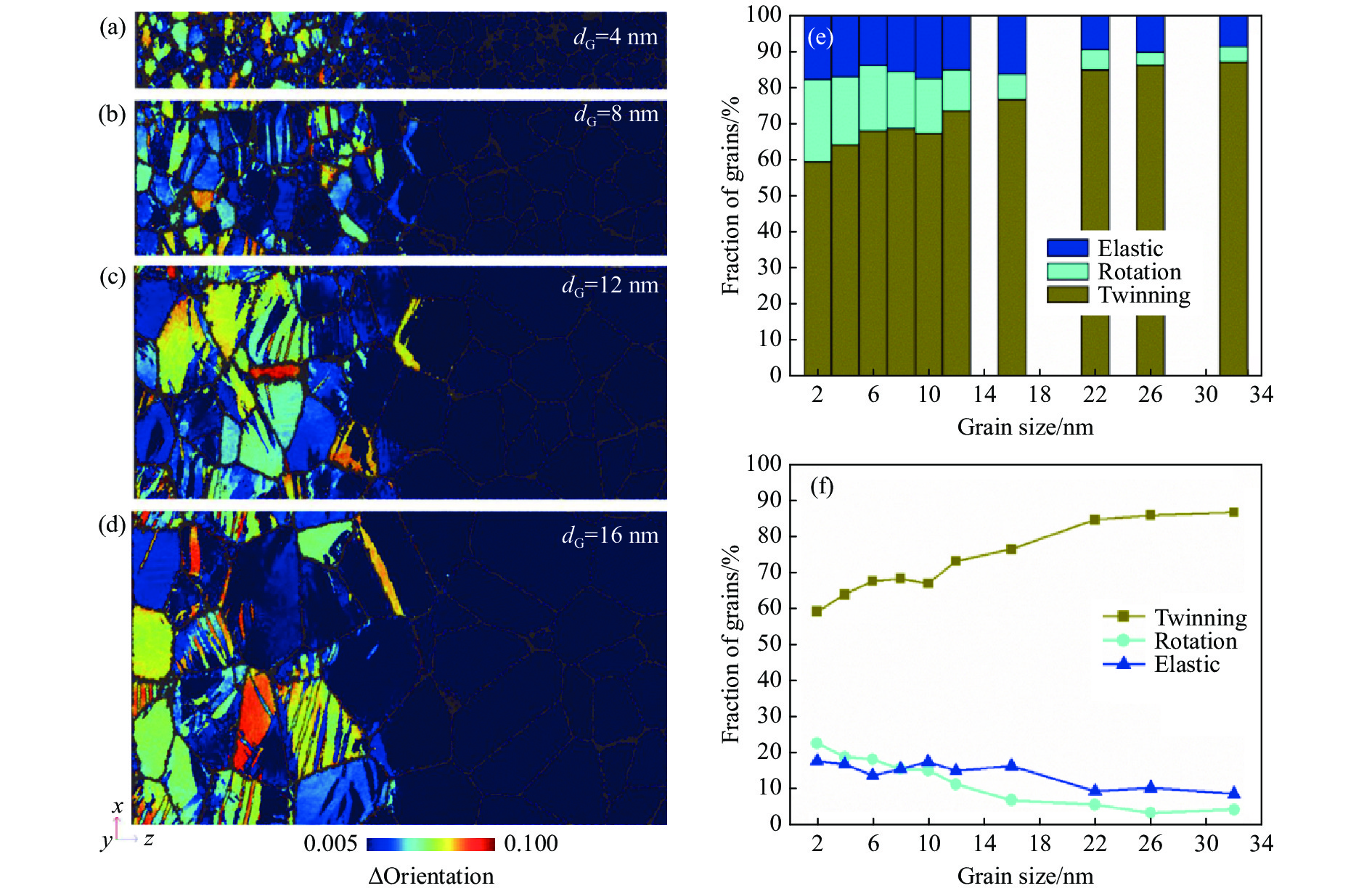
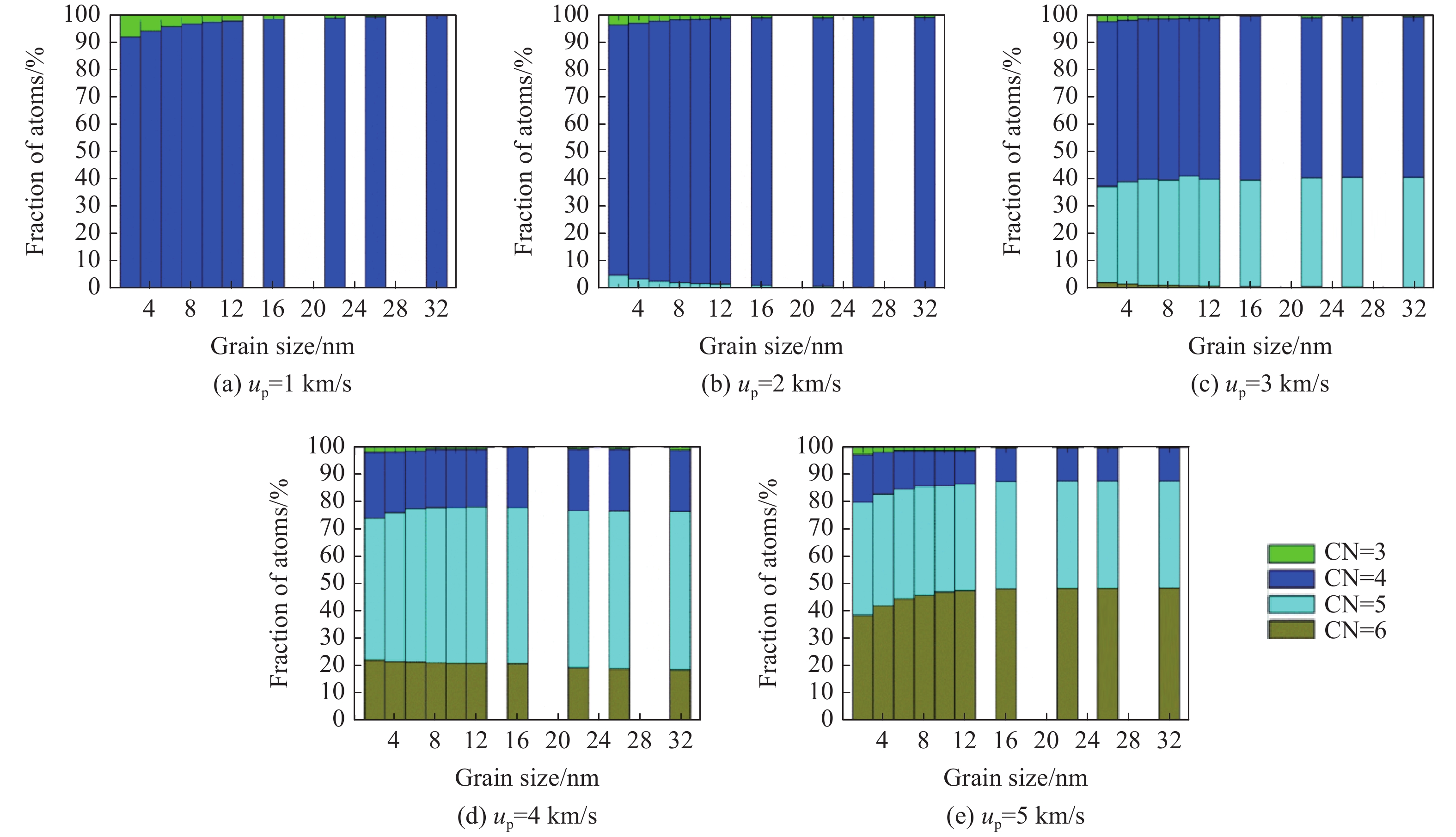
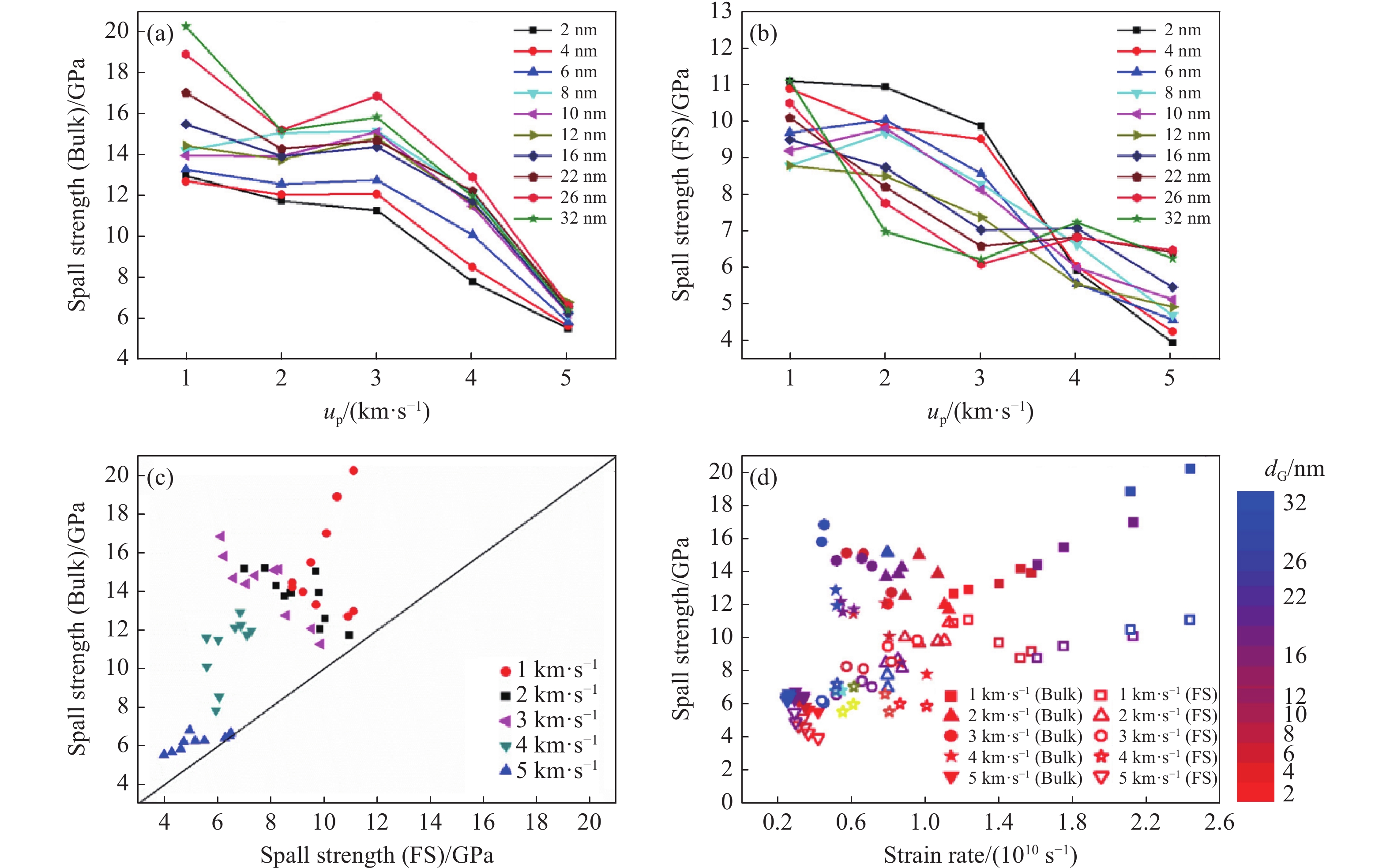
李旺辉等[143]进一步通过高达两亿原子的超大规模体系,实现了晶粒尺寸在2~32 nm范围的材料冲击响应模拟。如图28所示,当晶粒尺寸逐渐趋于小纳米尺度时,晶界的比例显著增加,而晶粒的比例则显著减小。该工作详尽地分析了晶粒尺寸对纳米多晶SiC材料冲击Hugoniot曲线、冲击塑性变形、冲击结构相变以及冲击层裂等物理和力学行为的影响规律。研究发现,粒子速度(up)为2 km/s的冲击压缩下变形孪晶是塑性变形的主要形式。随着纳米晶粒尺寸的减小,孪晶的形成逐渐变得困难,但在8 nm晶粒尺寸时出现反常现象,如图29所示。高强冲击诱发的结构相变在up为3~5 km/s范围内迅速发展,并在6 km/s时产生大规模的结构相变。图30显示了纳米晶粒尺寸对冲击结构相变的影响,小纳米晶粒尺寸在单一相变波结构(up = 6 km/s)中对结构相变的形成起到一定的抑制作用。此外,李旺辉等指出,在极高的应变率下基于原位测量的直接法和基于自由面粒子速度时程曲线的间接法在测量纳米多晶SiC陶瓷层裂强度的差异不可忽略,如图31所示,这两种方法分别对应极限抗拉强度和形核应力。
 图 28 (a) 样品中原子数-晶粒尺寸关系,(b) 密度和单位原子能量与晶粒尺寸的关系,(c) 晶粒或晶界中原子的比例作为晶粒大小的函数(黑色和红线分别为颗粒原子和晶界原子比例的理论预测)[143]Figure 28. (a) The number of atoms in samples as a function of grain size, (b) the density and per-atom energy as functions of grain size, (c) the fraction of atoms in grains or grain boundaries as functions of grain size (The black and red lines are the theoretical predictions of the fraction of grains and grain boundaries atoms, respectively.)[143]
图 28 (a) 样品中原子数-晶粒尺寸关系,(b) 密度和单位原子能量与晶粒尺寸的关系,(c) 晶粒或晶界中原子的比例作为晶粒大小的函数(黑色和红线分别为颗粒原子和晶界原子比例的理论预测)[143]Figure 28. (a) The number of atoms in samples as a function of grain size, (b) the density and per-atom energy as functions of grain size, (c) the fraction of atoms in grains or grain boundaries as functions of grain size (The black and red lines are the theoretical predictions of the fraction of grains and grain boundaries atoms, respectively.)[143] 图 29 (a)~(d)纳米多晶在不同晶粒尺寸下的冲击引起的晶体塑性变形,(e)~(f)不同晶粒尺寸的纳米碳化硅在up = 2 km/s时的冲击塑性统计[143]Figure 29. (a)–(d) Shock induced plasticity in nanocrystalline SiC with different grain size; (e)–(f) the statistics of shock induced plasticity at up = 2 km/s including twinning, rotation in nanocrystalline SiC with different grain sizes[143]
图 29 (a)~(d)纳米多晶在不同晶粒尺寸下的冲击引起的晶体塑性变形,(e)~(f)不同晶粒尺寸的纳米碳化硅在up = 2 km/s时的冲击塑性统计[143]Figure 29. (a)–(d) Shock induced plasticity in nanocrystalline SiC with different grain size; (e)–(f) the statistics of shock induced plasticity at up = 2 km/s including twinning, rotation in nanocrystalline SiC with different grain sizes[143]除SiC陶瓷外,类似的工作也涉及AlN、Al2O3等陶瓷材料。Branicio等[126]采用包含2.09 × 108原子的AlN陶瓷模型,进行了大规模MD模拟,在原子尺度上揭示了伴随AlN陶瓷结构相变的断裂机制。超高速弹丸冲击产生的冲击波分裂成双波结构,即弹性波后跟随着结构相变波,并触发了从纤锌矿结构到岩盐结构的转变,如图32所示。研究发现了两种独立的裂纹成核和生长机制,这两种机制都是在纤锌矿相-岩盐相界面处开始的。Branicio等[127]也对AlN陶瓷在0.8~4.0 km/s粒子速度范围内进行了平面冲击载荷MD模拟,结果也表明冲击产生了明显的双波结构,包括一个弹性前驱波和随后的结构相变波。但是,在他们的MD模拟研究中没有观察到变形孪晶或其他塑性波,这与以往的多晶AlN实验中的发现有偏差。Zhang等[129-131]对含有5.4 × 108原子的氧化铝样品进行了超高速撞击模拟。该模拟中弹体以18 km/s的超高速撞击时产生了与低应变率下的变形机制完全不同的对称性,揭示了一系列原子变形机制,包括锥体形式的滑移和各种孪晶变形。裂纹萌生源自材料的非晶化、结构相变和高应变率变形模式之间的相互作用。大量裂纹形核于微裂纹在先前变形的交叉点处并处于连接顶部和底部自由表面的沙漏形体积内。最后,层裂发生在无定形区和孪晶区的界面处。
从以上基于原子尺度的模拟研究可以看出,MD方法特别适合极端条件下材料动力学行为研究。对SiC而言,目前的研究可以较好地再现冲击实验Hugoniot曲线,也可揭示动态破坏的裂纹初始状态和扩展过程,但对于SiC的多形体特征研究尚有不足。然而,大多数冲击试验研究的对象为α-SiC陶瓷,而MD的模拟试样则多为β-SiC,无法形成有效对比。因此,相关研究有待进一步挖掘和完善。
2.3 基于第一性原理的高压相变计算
第一性原理计算及MD模拟作为常见的原子模拟方法,与基于牛顿运动方程的经典MD不同,原子核作为微观粒子以薛定谔方程进行描述,其“力场”直接来源于电子结构计算,而不依赖于经验势的拟合。相较于MD模拟,受计算效率的限制,第一性原理计算的体系尺度更小,模拟时间更短,但结果更加精确。Pizzagalli[147]就曾通过一系列第一性原理计算,研究了4H、2H和3C-SiC中位错的稳定性和迁移率。Lu等[148]对SiC压力诱导相变进行了第一性原理计算,结果表明:采用(PW91)GGA[149]交换关联势进行计算时,从能量-体积关系来看,SiC从闪锌矿结构向岩盐结构转变的压力为74.6 GPa,而通过焓计算得到的转变压力为75.4 GPa。Lee等[138]通过第一性原理计算,分析了SiC的高压相变和相关热力学性质,采用PBE[150]和PBEsol[151]作为交换相关联势,重现了SiC从闪锌矿结构到盐岩结构的相变,并与先前不同赝势计算结果和实验结果进行比较。PBE在较长时期代表了非经验势发展的最高水平,虽然减少了局部自旋密度近似(LSDA)的过耦合,但是却经常高估晶格常数,因此对于体积模量、声子频率等仍然存在过度校正的问题。PBEsol是在PBE的基础上进行的修正,大幅降低了计算过程中对平衡态晶格常数的高估,但对原子化能的计算精度低于PBE。计算发现,这两种赝势在计算SiC的平衡性质中都显示出合理的结果,但在计算晶格常数、体积模量和弹性常数等参数时PBEsol比PBE更准确,用PBEsol赝势得到的立方SiC相变压力为58 GPa,低于PBE的67 GPa。最近,Gorai等[152]采用杂化泛函B3LYP[153]计算了SiC的状态方程参数,预测了3C-SiC和6H-SiC分别在102和105 GPa发生冲击诱导相变至岩盐型结构相。这也是目前通过第一性原理计算得到的与实验值最吻合的结果。
3. SiC等陶瓷材料的多尺度模拟
多晶材料的微结构对控制材料的力学响应至关重要,细晶强化效应、裂纹萌生与扩展等问题均与晶粒尺寸及其分布、晶界特征等密切相关。因此,计算模拟中想要全面准确地描述多晶材料的变形和力学响应,就需要模型中有足够准确的材料微结构特征信息。构建材料性能与微结构之间的复杂关系是长期以来人们的研究目标,极具挑战性。多尺度模拟是实现该目标的重要手段,已成功应用于材料的变形和力学响应模拟,尤其是材料的断裂破坏行为研究。
多尺度模拟手段具有多种不同形式。通常而言,按照方法论,可以分为顺序多尺度方法和共时多尺度方法两类[154-155]。顺序多尺度方法中,材料信息从小尺度开始逐级传递给大尺度,不同尺度的研究有先后之分,即先从小尺度层面对材料属性进行研究,得到有用的结论和参数;然后将这些结论和参数作为先验已知的物理量或参数,在大尺度下对材料开展研究。例如,基于有限元(FEM)的模拟中引入的黏结域(CZM)所需参数可从MD模拟中获得。通过小尺度对双晶材料的拉伸或剪切模拟,可以获得相应的牵引力-位移关系,进而传递给大尺度有限元模拟,实现顺序多尺度方法。共时多尺度方法则是将不同尺度的模拟同时用于材料模拟。在裂纹扩展问题中,裂纹尖端及周边采用MD方法模拟,而在更大的范围内采用有限元方法模拟,两者之间采用一定的绑定桥联作用耦合起来。
Li等[156]曾指出,集成原子尺度和介观尺度的模拟技术对系统理解材料强度受缺陷微结构的影响至关重要。离开介观时空尺度,人们很难合适地建立起材料强度变化与材料微结构的关系。为了桥连这些空间尺度,在有限元里嵌入MD模块依旧是一个吸引人的方向,但是在耦合两个区域并保证不产生非物理的影响方面尚缺乏丰富的经验[157]。而为了桥连时间尺度,结合原子模拟和动力学蒙特卡罗方法是潜在可行的办法,但它仍然存在同样的问题,即需要了解如何最合适地将原子模拟获得的活化能融入没有原子的粗颗粒模拟中[158]。该问题存在的挑战是如何在确保外荷载的作用下仍然使缺陷微结构具有足够高的自由度,以更自然的方式响应外荷载作用,从而理解缺陷演化的驱动力与外荷载之间的关系。
Dong[159]基于多尺度模拟方法对陶瓷材料的性质进行模拟研究,桥连了量子水平、原子尺度、微观和宏观尺度的陶瓷材料模拟。他基于第一性原理方法,获得了更准确的原子间势函数,并提供给MD模拟。通过MD模拟获得了玻璃相界面的性质,包括牵引力-位移关系。该界面性质进一步用于有限元计算中黏结域的参数化。为了降低计算成本,他提出基于材料基因组的多尺度模型,即将多尺度模型与变分渐近方法耦合,用于单位单元均质化(VAMUCH),以预测陶瓷的材料性能。由此预测了氧化铝陶瓷、SiC陶瓷和SiC/SiC复合材料的机械性能和热性能,通过对比模拟结果与实验测量结果,证实了多尺度模型的有效性。Yamashita等[160]对MD和一些多尺度方法进行了综述,包括与温度相关的纳米尺度-连续介质方法的均质化技术和桥接域偶联方法。
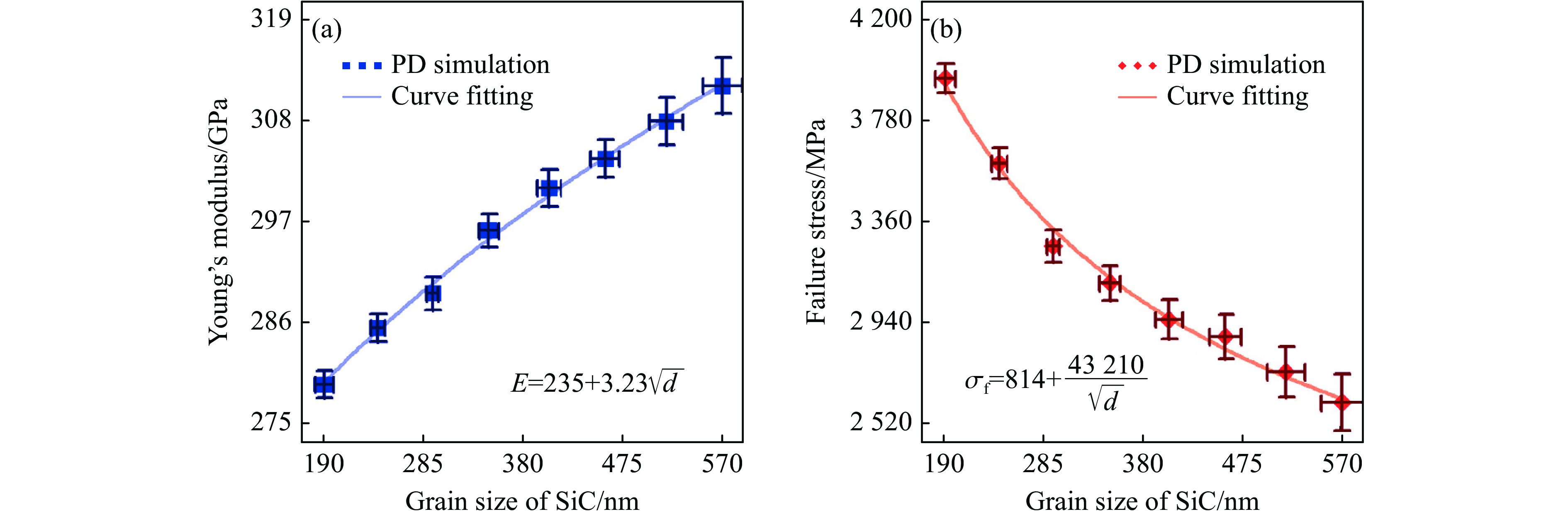
Gur等[161]采用近场动力学(PD)-MD方法,构建了原子尺度到介观尺度的多尺度模拟方法,研究了不同晶粒尺寸的多晶SiC的破坏断裂行为。在该研究中,多尺度模式属于顺序多尺度方法,见图33。PD-MD模拟的多晶SiC中,不同晶粒和晶界是随机分配的,其性质来自MD结果。具体而言,与PD模拟密切相关的两个参数s0和c分别与能量释放率和体积模量相关,来自对不同双晶和单晶的MD模拟结果。基于该多尺度模拟,结果显示,在200~550 nm的晶粒尺寸变化范围内多晶SiC的断裂强度呈现霍尔-佩奇(Hall-Petch,HP)关系,如图34所示。
除了从MD和第一性原理出发的多尺度模型,也有更高尺度之间的多尺度建模工作。由于多晶陶瓷的强度性能和冲击状态下的非弹性变形机制对陶瓷在装甲结构方面的设计和优化有重要作用,Zhu[106]通过宏观-介观多尺度建模,研究了平板冲击下微结构、晶体各向异性、孔隙强度对多晶陶瓷冲击响应的影响及其相互作用机理,采用介观尺度计算模型,检验了颗粒内部微塑性和变形孪晶、晶间微损伤和孔隙对非弹性变形和冲击强度的影响。结果表明,对AD995陶瓷而言,孔隙率对冲击强度的降低作用比玻璃相晶界更显著。由孔洞引起的基面孪生和棱柱面滑移可以很好地模拟其冲击响应。在宏观层面上,提出了一个结合非线弹性和与压力相关的塑性均质连续模型,通过匹配材料(AlON和多晶6H-SiC)确定材料参数,实现了对冲击波剖面测量值的模拟仿真。
4. 纳米多晶SiC等陶瓷材料的变形与破坏机理
硬质单晶及纳米多晶陶瓷无论是在强度、韧性还是塑性方面均显著优于粗颗粒传统陶瓷。Szlufarska等[163]综述了极端条件下陶瓷材料的力学性能,指出纳米陶瓷受晶界的影响很大,而极端环境中的高压冲击加载又能引起许多与低压环境不同的独特变形机理,如位错塑性、孪晶、相变以及无定形化等。这些机理一般是由原子尺度变形过程控制的,往往小于晶粒尺寸。相反,低压环境中其变形和失效模式通常是由微裂纹主控的。这些微裂纹从缺陷处形核,而这些缺陷往往比晶粒尺寸更大,微裂纹的尺寸也相对更大。要想有效地平衡这些问题,需将晶粒尺寸视为一个特征长度尺寸,低于该尺寸时塑性变形机制被激活,而高于该尺寸则断裂机制被激活。当然,断裂机理中也可能存在穿晶断裂。因此,对于晶粒尺寸低至纳米级别的多晶陶瓷,新的力学现象和变形机制可能会被激发。不同的晶粒尺寸将决定极端环境下陶瓷等脆性材料力学响应问题的研究方向[164]。
与晶粒尺寸有关的典型现象之一就是HP关系[162, 165-167],最早于20世纪50年代提出[168-169],用于描述晶粒尺寸相关的屈服应力。在许多金属材料的实验研究中都发现了强度或硬度随晶粒尺寸的减小而增强的现象[170-172],即HP关系。这些现象被认为是多晶金属中的位错在晶界处堆积引起的[167]。当晶粒尺寸减小至纳米级别时,反Hall-Petch(IHP)效应出现了[173-174]。用于解释该现象的多种理论模型相继被提出,包括基于位错的模型、基于耗散的模型、晶界剪切模型和两相模型[175-177]。纳米金属材料的广泛系统研究揭示了在强度、硬度、孪晶应力等性质方面从HP关系到IHP效应的转变,HP关系的失效大部分集中在晶粒尺寸为10~20 nm之间的狭小范围[178-180]。对陶瓷材料而言,晶粒尺寸同样会影响其物理力学性质[181]。尽管HP关系在传统陶瓷材料中已有发现,但对纳米陶瓷的HP失效问题研究极少,仅集中在MgO[182]和MgAl2O4[183-186]陶瓷。即便是同一种陶瓷的研究结果,也存在相互矛盾,且临界晶粒尺寸可相差一个数量级(30~130 nm)[183-184]。值得注意的是,广泛讨论的HP关系或IHP效应大多数是在准静态拉伸或压痕实验或模拟条件下进行的,极少有冲击情况[187]。实验表明,纳米多晶材料比其大颗粒材料的应变率敏感性更高。固体中的冲击层裂涉及冲击波压缩、应力波传播和反射的相互作用、初始动态拉伸损伤、断裂演化和失效等复杂过程。相比于准静态行为,冲击层裂在压缩和拉伸阶段都伴随着高应变率,可能会影响HP关系或者IHP效应。Vo等[188]通过模拟研究发现,高应变率下纳米材料的屈服强度不仅与晶粒尺寸有关,而且还依赖晶界的弛豫状态。Wilkerson等[189-190]的研究表明,对于金属材料,冲击引起的形核应力存在不同寻常的晶粒尺寸效应。他们提出的理论模型描述了这种耦合晶粒尺寸和应变率的强度关系,其结果不仅证实了纳米多晶材料比粗颗粒材料有更高的应变率敏感性,而且也指出从IHP到HP转变的临界晶粒尺寸与应变率相关。传统细晶强化理论也继续受到反细晶强化理论的冲击[191],同时对不同晶粒尺寸和应变率下材料性质的研究也继续存在挑战性。
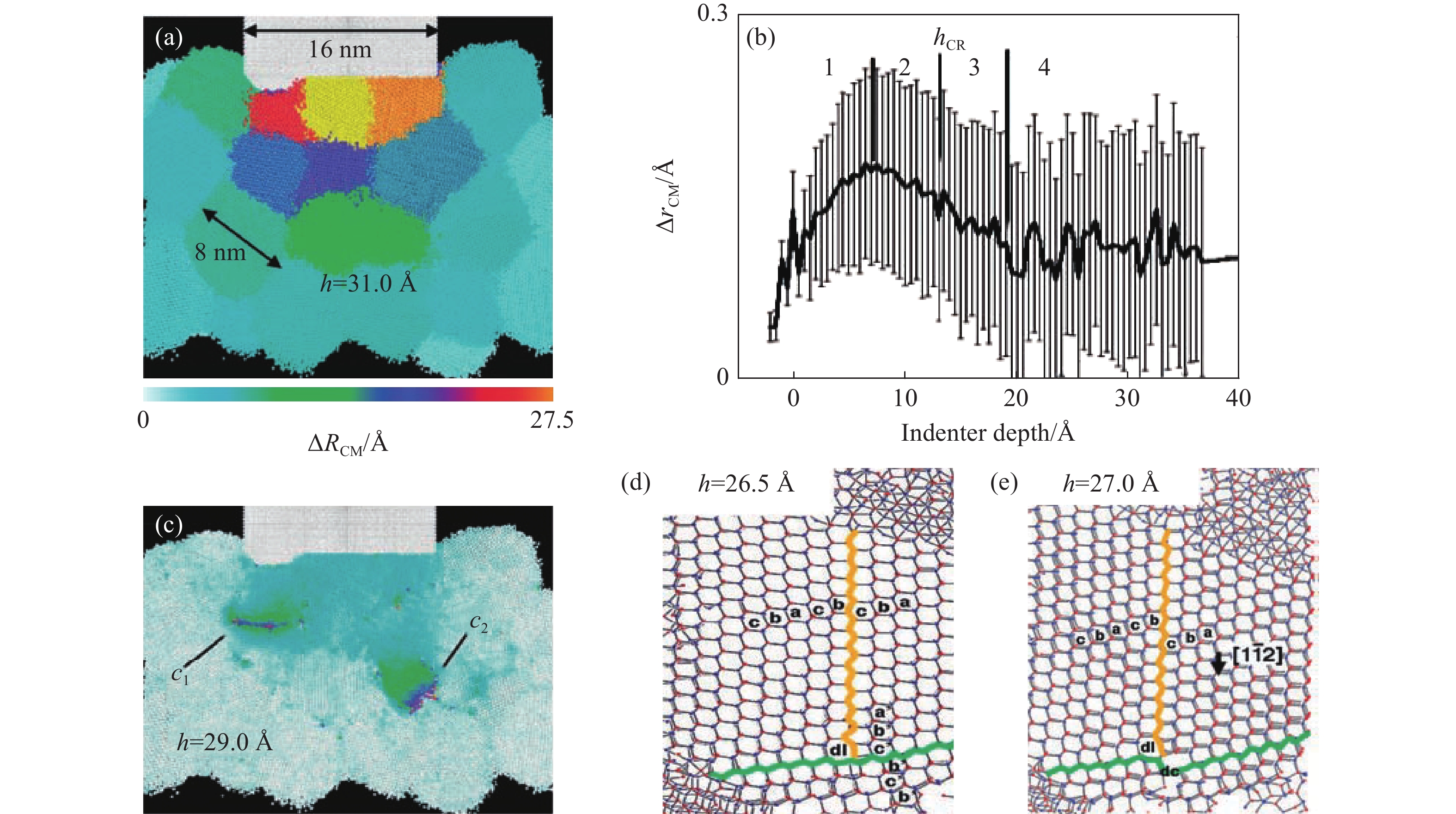
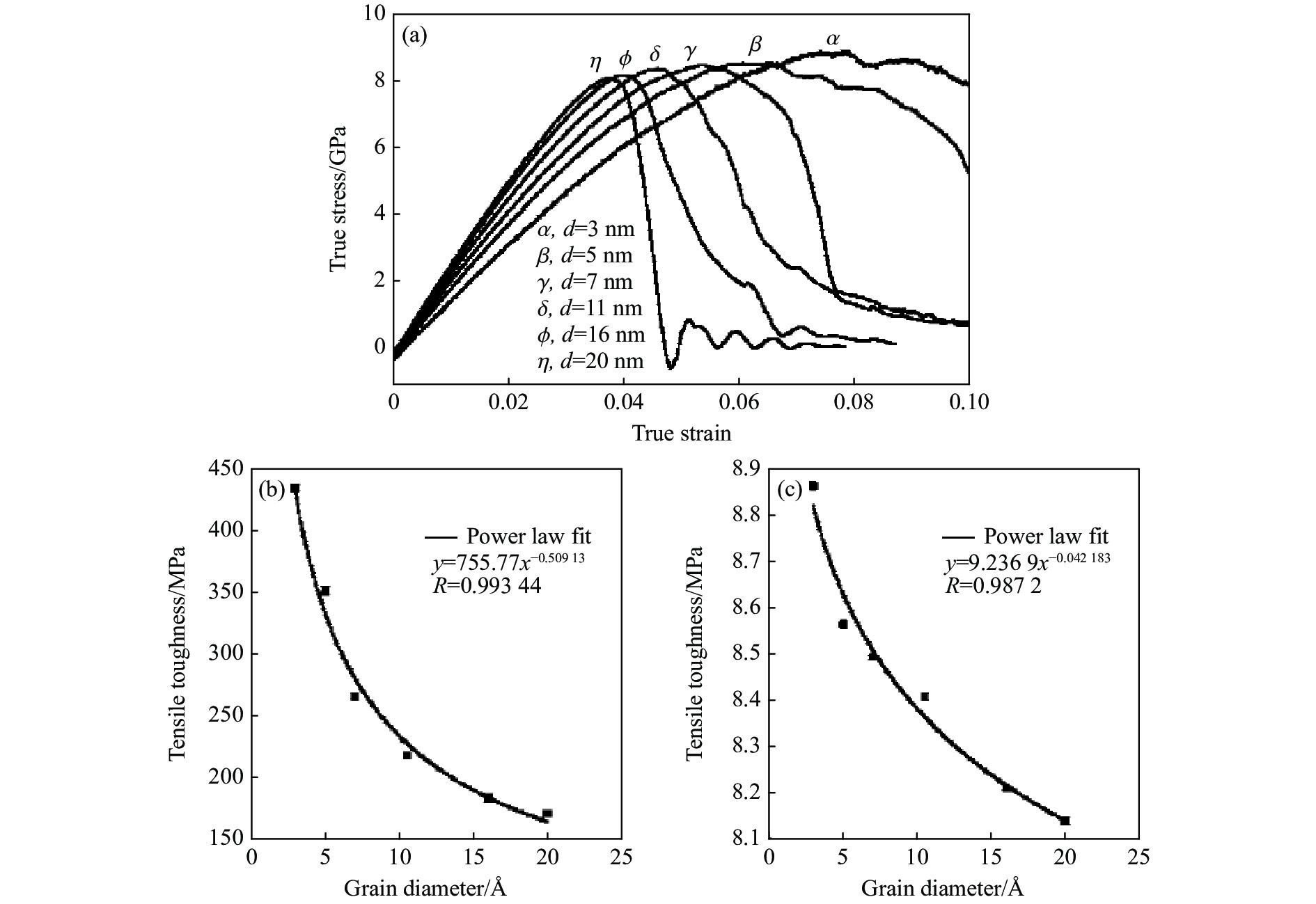
对纳米多晶SiC而言,早期Li等[156]通过MD模拟研究,预测了SiC极限拉伸强度的HP关系的失效问题,但他们没有具体分析临界晶粒尺寸,只是粗略地给出了预测值,约为20 nm。纳米多晶SiC薄膜的纳米压痕实验[192]表明,晶粒尺寸在5~20 nm区间时,材料呈现超高硬度。当平均晶粒尺寸为10~20 nm且晶粒体积分数在80%~85%之间时,纳米多晶SiC的硬度可达50 GPa,远高于块体SiC陶瓷的30 GPa。基于百万原子规模的MD模拟,纳米多晶SiC的纳米压痕模拟研究[193]预测了在某临界压痕深度,晶粒内连续变形和晶粒间离散变形存在交叉机制,如图35所示。这种交叉源于晶粒滑移、旋转和粒间位错之间的相互作用。该纳米多晶SiC的平均晶粒尺寸为8 nm,且硬度为39 GPa。纳米多晶SiC在108 s−1应变率下的单轴拉伸MD模拟结果[194]显示,晶粒尺寸的降低可同时提高材料的延性、韧性和拉伸强度,如图36所示,并认为这是晶粒间断裂时在原子尺度发生颈缩的缘故。在晶粒尺寸为200 nm的纳米SiC拉伸实验中也发现了高温下的超塑性[195]。通过高分辨率TEM没有观察到晶界处存在第二玻璃相,因此他们认为晶粒间的玻璃相并非共价键材料获得超塑性的必要条件。在动态压缩的纳米Si3N4中也发现了超塑性[196]。最近,MD模拟研究晶粒尺寸为2~8 nm的纳米多晶SiC的拉伸[197]时显示,材料不仅变得具有延性,而且当晶粒尺寸降低至2 nm、应变率为106 s−1时,预测室温下也可以实现超塑性变形,如图37所示。
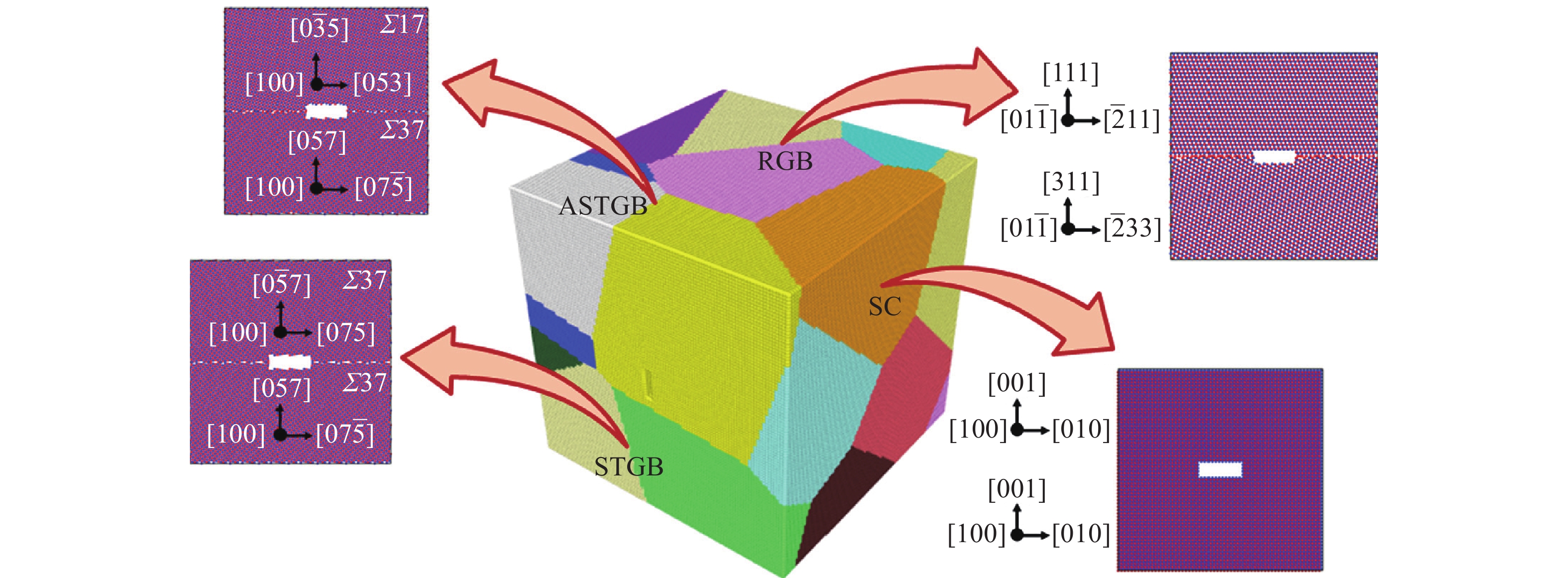
上述纳米多晶SiC陶瓷研究表明,在陶瓷晶界上仍存在未解决的问题,为了在纳米晶陶瓷中获得良好的延展性和韧性而对晶界进行工程设计是复杂且极具挑战性的。这需要研究纳米多晶SiC中的晶界,以揭示超塑性、延展性和韧性的变形机理,并指导先进纳米晶陶瓷设计。纳米多晶SiC中的晶界至关重要,这是因为原子尺度的键合和晶界的结构性质对依赖于微结构的材料性能的影响重大。临界裂纹长度的增加和断裂韧性的改善在小纳米颗粒尺寸和高晶界取向角的情况下尤为显著。常规(非无序)晶界的典型厚度约为1 nm,而非晶晶界的厚度在1 nm至几纳米范围内。晶界的原子结构和性质不同于晶粒的结构和性质。通过高分辨率透射电子显微镜(HRTEM)可观察到SiC存在多种晶界[198],晶界结构取决于与多型性有关的生长机制。从能量角度上看,通常对称晶界比非对称晶界更稳定,而晶界指数低的小平面更可取。到目前为止,仅有少量非对称晶界的研究工作。
纳米孪晶是纳米微结构的重要形式之一。通过引入能量低、对称性高的共格孪晶晶界,纳米孪晶金属材料可实现强韧化等多力学性能提升[199-201]。然而,目前关于纳米孪晶对陶瓷或半导体材料力学性能和变形机制影响的认识有限[202]。第一性原理计算显示,通过引入纳米孪晶,立方碳化硼的理想剪切强度、硬度和断裂韧性可提高11%[203],但纳米孪晶对碳化硼却起到软化作用,剪切强度反而降低[204]。类似地,纳米孪晶微结构可提升亚氧化硼的剪切强度[205-206],对Bi2Te3和InSb的剪切强度分别提高215%和11%[207-208],但对Mg2Si却起着软化作用[209]。对于SiC而言,实验室已成功制备出具有周期性纳米孪晶特征的立方SiC纳米结构[210]。相比金属中由于位错与共格孪晶晶界的相互作用而使强度和韧性同时得以提高的情况,SiC因具有很强的共价键特性而呈现不显著的位错运动,从而影响纳米孪晶陶瓷的力学行为和变形机理。纳米尺度的塑性相关实验已经说明晶体结构与缺陷运动相互作用的重要性。合成周期性孪晶3C-SiC纳米线的压缩性实验表明[211-212],体积模量增加到316 GPa,比其他形态(包括微米和纳米尺寸的颗粒以及无孪晶纳米线)的3C-SiC高20%~40%。MD模拟研究显示,(111)取向3C-SiC纳米线的屈服强度临界应变可通过孪晶增强,并且临界应力随着孪晶边界间距的减小而增加,但低于无孪晶缺陷的材料。
已有的实验报告指出,5 nm厚孪晶层的纳米孪晶金刚石展现出了超高的硬度(200 GPa)和断裂韧性(14.8 MPa·m1/2)[213]。这种超硬特征被认为是纳米孪晶中纳米尺度的HP效应和量子约束效应共同决定的,而断裂韧性的提升则是沿密排孪晶界的位错滑移引起的。纳米压痕的MD模拟揭示了传统HP增强关系是由于孪晶界阻碍了位错运动进而导致硬度提升,而软化的原因则是平行位错环的形成和运动提供了新的位错形核点[214]。
Chavoshi等[215]基于MD方法开展了纳米孪晶、单晶和多晶立方SiC的纳米压痕试验,如图38所示。研究结果表明,纳米孪晶单晶的优异纳米接触电阻源于共格孪晶晶界的晶格位错阻挡效应,并且与共格孪晶晶界密度有明显的相关性。当平均晶粒尺寸大于8 nm时,纳米孪晶纳米晶体表现出类似反HP的作用,而细晶粒尺寸的纳米孪晶纳米晶体与无孪晶的纳米晶体相比,压痕硬度略有提高。他们认为,无论共格孪晶晶界间距如何,晶粒边界、晶格位错滑移和共格孪晶晶界共同适应了压头在大晶粒纳米晶体基底中施加的塑性应变。然而,随着晶粒尺寸的减小,晶格位错和共格孪晶晶界的贡献变得有限。该工作揭示了晶格位错与共格孪晶晶界的相互作用机制,即孪生部分位错的成核以及共格孪晶晶界处点缺陷的形成和湮灭对测试条件(温度、压痕速度和压头尺寸)不敏感。但随着共格孪晶晶界间距的减小,孪晶位错通过大多数Shockley部分而不是困在共格孪晶晶界处的Frank部分的解离和传播而发生。Chavoshi等[216]基于MD研究了纳米孪晶立方SiC在不同应力状态下的力学响应和变形机理转变。如图39所示,研究发现,不同的应力状态、晶体或孪晶方向以及孪晶间距的组合体激活了不同的变形机制,包括:孪晶附近的点缺陷形成和位错滑移控制的剪切局域化和剪切破坏;没有任何位错塑性特征的解理断裂破坏;在孪晶之间发生严峻的局域变形,不经任何结构相变或无定形化却形成独特的锯齿形微结构;在共格孪晶晶界附近产生局域无序结构,激发了位错形核,降低了抗剪性能。
 图 39 (a)~(d) λ= 1.5 nm时样品在剪切诱导下的结构演化;(e)~(h) λ= 3 nm时样品在单轴压缩下的微观结构演化[216]Figure 39. (a)–(d) Shear-induced fracture in the nanotwinned sample with λ = 1.5 nm subjected to uniaxial compressive loading; (e)–(h) microstructural evolution of the nanotwinned sample with λ = 3 nm subjected to uniaxial compressive loading[216]
图 39 (a)~(d) λ= 1.5 nm时样品在剪切诱导下的结构演化;(e)~(h) λ= 3 nm时样品在单轴压缩下的微观结构演化[216]Figure 39. (a)–(d) Shear-induced fracture in the nanotwinned sample with λ = 1.5 nm subjected to uniaxial compressive loading; (e)–(h) microstructural evolution of the nanotwinned sample with λ = 3 nm subjected to uniaxial compressive loading[216]5. 总结和展望
SiC凭借高比强度、高硬度和高熔点等特点在航空航天、国防军事等领域发挥了重要作用,碳和硅原子的键合形式及其多态性使之成为高压地球物理和星系研究的重要介质。因此,SiC的动力学行为和高压特性研究具有重要的科学意义和工程价值。本文分别从实验、模拟与理论计算方面概述了以SiC为代表的陶瓷和半导体材料的动态物理力学行为研究进展。
综上表明,目前已初步形成了跨尺度的多样化研究,从SHPB实验、轻气炮驱动平板冲击实验、磁驱动实验到激光脉冲加载实验,对不同试样尺寸实现了较宽范围的应变率加载。与此对应,在不同的时间和空间尺度上,对SiC的模拟研究也涉及基于连续介质的宏观尺度、基于原子模拟的微纳米尺度以及基于第一性原理的量子尺度的计算。通常情况下,连续介质模拟方法可全尺度比照SHPB实验和平板冲击实验,展现材料宏观特性,原子模拟方法如MD则可以匹配激光脉冲加载实验研究的时空分辨率,揭示微纳观尺度的变形行为。然而,当前的研究现状仍然存在以下主要问题。
(1)实验方面,受限于各时期材料工业制备及工艺水平的发展,材料存在不同程度的缺陷。样品微结构的多样性使实验数据具有较大的离散性。不同类型的动态实验覆盖了不同的应变率区间,不同研究方法下材料强度等实验结果的关联性及材料动力学行为跨时空尺度科学问题仍然缺乏深入探讨和分析。
(2)计算模拟方面,各种方法均有优缺点。基于连续介质的计算模拟依靠准确的动态本构和状态方程可实现全尺度模拟,但方程的诸多参数受限于特定实验而影响了其可预测性。基于原子计算的微纳观尺度模拟或基于量子的第一性原理计算可以直接得到多种关键的物理参量,揭示微纳米尺度的变形和破坏机理。但目前大规模MD模拟一方面需要基于可靠的原子间相互作用势,另一方面需要使用强大的计算资源,这也受到超级计算机发展的限制。同时,不同计算方法之间多尺度、跨尺度的耦合尚处于初步发展阶段,仍未形成统一认知。
(3)物理机理方面,变形与破坏机理的复杂性在于影响因素众多,包括晶粒尺寸、晶界结构、特定微纳结构(如位错、纳米孪晶等),这些因素对变形机理的影响与材料种类相关,对于SiC,尚缺乏系统全面的机理分析。
总之,尽管以往的实验和模拟研究为了解SiC陶瓷的动态力学行为提供了许多有益的参考,但是在更广阔的应用需求以及更加严峻的服役环境下,仍然存在诸多重要的科学问题值得探索。SiC作为重要的陶瓷材料和极具应用前景的半导体材料,是地球物理和宇宙物理研究中的重要介质,对SiC的研究吸引了诸多领域的研究人员。然而,由于其存在形式非常复杂,从传统的SiC陶瓷到先进的纳米SiC和单晶硬质陶瓷,影响其力学特性的因素很多,围绕强度与韧性、变形和破坏问题仍有诸多基础性问题尚未明确解决。随着生产技术和国防科技的发展,全面系统地研究性能更优越的硬质单晶和纳米多晶SiC陶瓷的必要性日益增加。相比于金属材料,先进陶瓷和半导体材料的动力学问题研究明显不足,未来仍然有多方面问题亟待解决和完善。现提出以下几个方面问题,期望为今后的研究提供有益参考。
(1)实验技术方面,动态加载下SiC等陶瓷或半导体材料的塑性和相变等物理力学响应是压力与温度耦合的结果,同时也受应变率等因素的影响。开展不同热力学加载路径加载下的动力学特性研究有助于在一定程度上实现压力-温度解耦分析,为理解压力和温度对材料塑性和相变的影响提供更深的认识。例如,斜波加载或准等熵加载技术作为近些年发展起来的先进动高压实验技术,在超高压、高应变率下材料的塑性与相变机制探索、物态方程测定、强度和本构关系研究以及核武器物理基础研究等众多领域发挥了重要作用。与冲击加载产生的高温高压情况不同,其在实现动高压的同时尽可能地减少了温升。其中,磁驱动[217-218]和激光驱动[13, 219-221]的斜波加载技术是当前实验室中实现斜波加载的最先进方式。目前,斜波加载或准等熵加载实验主要集中在金属材料研究[222-224],对非金属类材料研究较少。这些先进的斜波或准等熵压缩技术有望进一步拓展至更多重要的高压材料动力学研究中。SiC作为高压研究的重要材料,具有很高的相变压力,但高温作用也会降低其相变阈值[145, 225]。对SiC在极高压下的物质状态研究有助于为探索地球内核以及外星系等前沿领域提供重要的信息。此外,开展极端加载下的动力学特性研究有助于探索物质在更极端条件下的状态,为材料在极端苛刻服役条件下的性能评估和材料设计提供理论基础。
(2)计算与模拟方法方面,建立有效的多尺度方法是重要的发展趋势,从量子力学、MD出发,发展和完善适用于陶瓷类材料在极端条件下的原子间相互作用势。充分利用不同方法的优势,逐步构建跨尺度的方法,建立SiC等陶瓷和半导体材料的耦合多因素的跨尺度动力学模型,为材料强度、变形与破坏等跨尺度问题提供可靠的预测。
(3)从材料设计角度,基于微结构的复杂程度,如晶界结构的复杂性,可考虑引入包括机器学习在内的新手段实现对陶瓷晶界特性的预测,代替数量庞大的晶界结构种类分析,进一步用于顺序多尺度方法,提高参数传递的准确性和可靠性,逐步实现始于底层的多尺度材料和结构的设计。
-
Borisov A A, Khasainov B A, Veyssiere B. On Detonation of Aluminum Dust in Air and Oxygen [J]. Sov J Chem Phys, 1992, 10(2): 369-402. Zhang F, Gronig H. Transition to Detonation in Corn Starch Dust-Oxygen and -Air Mixtures [J]. Combust Flame, 1991, 86(1-2): 21-32. Zhang F, Gronig H. Two-Headed Detonation in Reactive Particle-Oxidizing Gas Flow [J]. Phys Fluids A, 1992, 4(10): 2308-2315. Zhang F, Gronig H. Spin Detonation in Reactive Particles-Oxidizing Gas Flow [J]. Phys Fluids A, 1991, 3(8): 1983-1990. Hui J M, Liu R H, Ge G L. Study on Increasing the Power of FAE (Ⅰ)-Selection of High Energy Fuels [J]. Journal of Nanjing University of Science and Technology, 1995, 19(5): 472-476. (in Chinese) 惠君明, 刘荣海, 葛桂兰. 提高FAE威力的研究(Ⅰ)--高能量燃料的选择 [J]. 南京理工大学学报, 1995, 19(5): 472-476. Mogi T, Horiguchia S. Explosion and Detonation Characteristics of Dimethyl Ether [J]. J Hazard Mater, 2009, 164(1): 114-119. Xu X F, Xie L F, Peng J H, et al. Study on the Detonation Cellular Structure of Propylene Epoxide-Air [J]. Explosion and Shock Waves, 2004, 24(2): 158-162. (in Chinese) 徐晓峰, 解立峰, 彭金华, 等. 环氧丙烷-空气混合物爆轰波胞格结构的研究 [J]. 爆炸与冲击, 2004, 24(2): 158-162. Liu Q M, Bai C H, Jiang L, et al. Deflagration-to-Detonation Transition in Nitromethane Mmist/Aluminum Dust/Air Mixtures [J]. Combust Flame, 2010, 157(1): 106-117. Liu Q M, Li X D, Bai C H. Deflagration to Detonation Transition in Aluminum Dust-Air Mixture under Weak Ignition Condition [J]. Combust Flame, 2009, 156(4): 914-921. Jiang L, Bai C H, Liu Q M. Experimental Study on DDT Process in 3-Phase Suspensions of Gas/Solid Particle/Liquid Mist Mixture [J]. Explosion and Shock Waves, 2010, 30(2): 588-592. (in Chinese) 蒋丽, 白春华, 刘庆明. 气/固/液三相混合物燃烧转爆轰过程实验研究 [J]. 爆炸与冲击, 2010, 30(2): 588-592. -

 点击查看大图
点击查看大图
计量
- 文章访问数: 8116
- HTML全文浏览量: 386
- PDF下载量: 671







 下载:
下载:







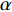
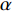








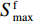


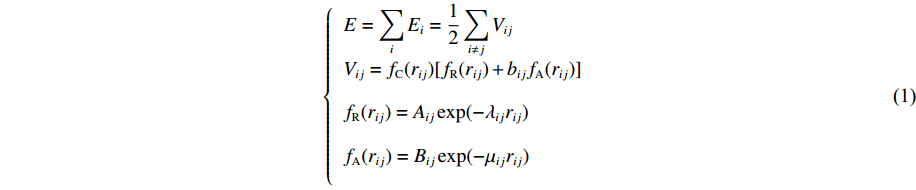
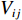
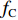
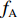
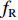
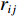
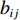
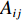
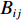
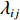
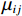
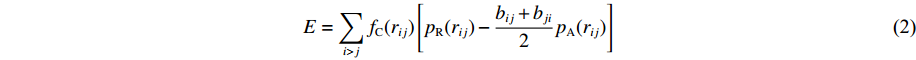
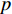
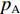
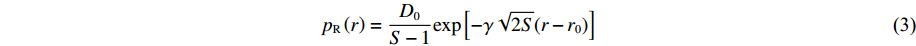
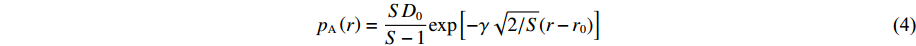
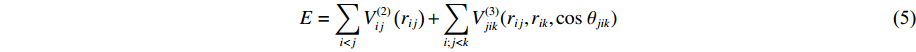
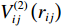
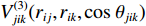
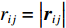
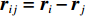
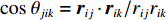
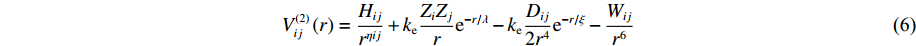
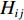
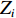
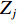
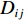
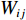
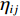
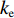
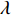
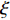

















 下载:
下载: