Crystal Structure and Stability of LiAlH4 from First Principles
doi: 10.11858/gywlxb.20170561
-
Abstract: The structural stability of LiAlH4, a promising hydrogen storage material, under high pressure was researched using the ab initio pseudopotential plane wave method.It is found that the phase transition occurs at 1.6 GPa from the α-LiAlH4 phase to the β-LiAlH4 (space group I2/b) phase.This phase transition is identified as first-order in nature with volume contractions of 18%.Moreover, the analysis of the phonon dispersion curves suggests that phase transition is related to the phonon softening.Mulliken population analyses indicated that the ambient phase (α-LiAlH4) is expected to be the most promising candidate for hydrogen storage.
-
海床已成为一个全新的冲突领域,近海底爆炸可以对海底光缆、海底管道等设施造成严重的破坏,其破坏过程涉及近海底反射、多相流掺混、结构与流体的耦合作用,开展近海底爆炸冲击波时空演化规律研究对于水中兵器研制及海底设施抗爆抗冲击设计具有重要的意义。
目前,国内外对近海底水下爆炸研究已经取得了一定成果。基于Kelvin的冲击理论,Blake等[1]得出了判断自由面附近气泡射流方向和气泡运动方向的方法,该方法对近壁面也同样适用。张永坤[2]对沉底水雷在水下爆炸作用下的毁伤情况进行了研究,总结了水雷在不同情况下被毁伤的特点,为提高水下灭雷武器的作战能力奠定了理论基础。邵建军等[3]基于相似理论,研究了海底对爆炸的影响,发现海底底质变化显著影响水下爆炸的冲击波能和气泡能。杨莉等[4–7]在泥底、砂底及石底3种条件下进行了沉底爆炸试验,发现在3种底质条件下,气泡后期溃灭形态存在差异,最大峰值压力通常出现在装药靠近水底面一侧的斜上方,对于爆距较小的水底面测点,反射波追上入射波会形成马赫波。黄潇等[8]采用镜像法模拟海底边界的影响,发现自由场爆炸气泡比近海底爆炸气泡对潜艇施加的总纵弯矩更大。姚熊亮等[9]基于光滑粒子流体动力学(smooth particle hydrodynamics,SPH)方法模拟沉底水下爆炸,研究了水底底质厚度和炸药当量对冲击波压力的影响。邵宗战等[10]提出了沉底水雷海上爆炸威力的测量方法,给出了冲击波峰值压力的拟合方法及爆炸能量计算方法。前人在近海底水下爆炸冲击波载荷分析方面已取得了一些成果,然而,针对不同底质条件下近海底水下爆炸冲击波载荷时空分布规律的定量研究尚不充分。
本研究拟采用耦合欧拉-拉格朗日(coupled Eulerian-Lagrangian,CEL)方法建立近海底水下爆炸模型,探讨不同底质条件下近海底爆炸冲击波的时空分布规律,以期为近海底设施的抗爆抗冲击结构设计提供支撑。
1. 数值模型与数值验证
1.1 状态方程
本研究采用TNT炸药,爆轰产物通过JWL方程[11]描述
p=A(1−ωR1v)e−R1v+B(1−ωR2v)e−R2v+ωev (1) 式中:A、B、R1、R2及
ω 为与炸药状态有关的常数,v为爆轰产物的相对比容,e为炸药单位质量所蕴含的内能。TNT炸药的材料参数及JWL状态方程参数如表1[12]所示,其中:ρ为密度,D为爆速。水采用Mie-Grüneisen状态方程描述,表达式[11]为
p=pH(1−Γ0η/2)+Γ0ρ0Em (2) 式中:pH为Hugoniot压力;ρ0为初始密度;Em为单位质量内能;Γ0为Grüneisen常数;η为名义体积压缩应变,
η=1−ρ0/ρ 。pH的表达式[11]为pH=ρ0C20η(1−Sη)2 (3) us=C0+Sup (4) 式中:us为冲击速度,up为粒子速度,S和C0为us-up曲线参数。水的状态方程参数列于表2[12]。
在数值模型中,设空气为理想气体,其状态方程[11]为
p+pa=(γ−1)ρEm (5) Em=cV(θ−θz) (6) 式中:γ为绝热指数,pa为外界压力,cV为比定容热容,
θ 为当前温度,θz 为绝对零度。空气的状态方程参数如表3[12]所示。1.2 数值模型
为研究近海底水下爆炸冲击波的传播规律,建立了数值模型,欧拉域尺寸为15.0 m×6.5 m×15.0 m,模拟50 kg TNT在50 m水深处的近海底爆炸,TNT底部距海底0.05 m。将整个欧拉域的边界条件设置为流出无反射,海底底质采用模型1或模型2描述。模型1是一种较软的土壤模型,参考了Ambrosini等[13]和Luccioni等[14]的研究结果,具体参数见表4[13–14],其中:E为杨氏模量,ν为泊松比,φ为内摩擦角,c为黏聚力。模型2为刚性固壁,通过在欧拉域中的海底底质区域放置拉格朗日刚体实现。
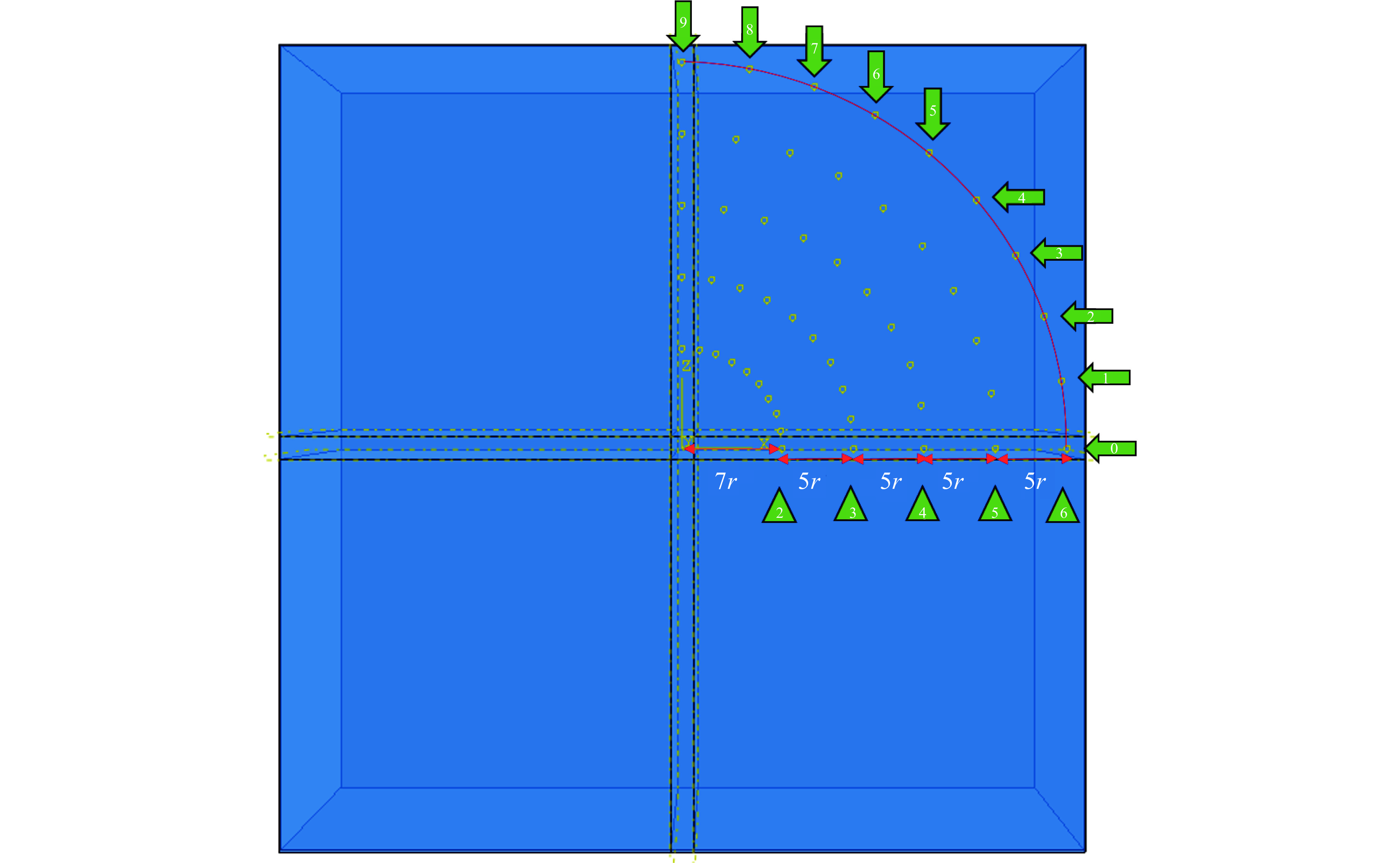
为了更准确地获得同一位置的冲击波压力,在模型的不同位置设置测点,测点布局如图1所示。设装药半径为r,测点到爆心的距离为R,测点与水平方向的夹角为测点角度α。在距离爆心分别为7r、12r、17r、22r、27r,测点角度分别为0°、10°、20°、30°、40°、50°、60°、70°、80°、90°处布置测点,共计50个测点。为方便后续分析,用测点距爆心的距离(爆距)以及测点角度命名测点,爆距7r、12r、17r、22r、27r用数字2~6表示,测点角度0°~90°用数字0~9表示,例如:将爆距为7r、测点角度为0°的测点命名为2-0。
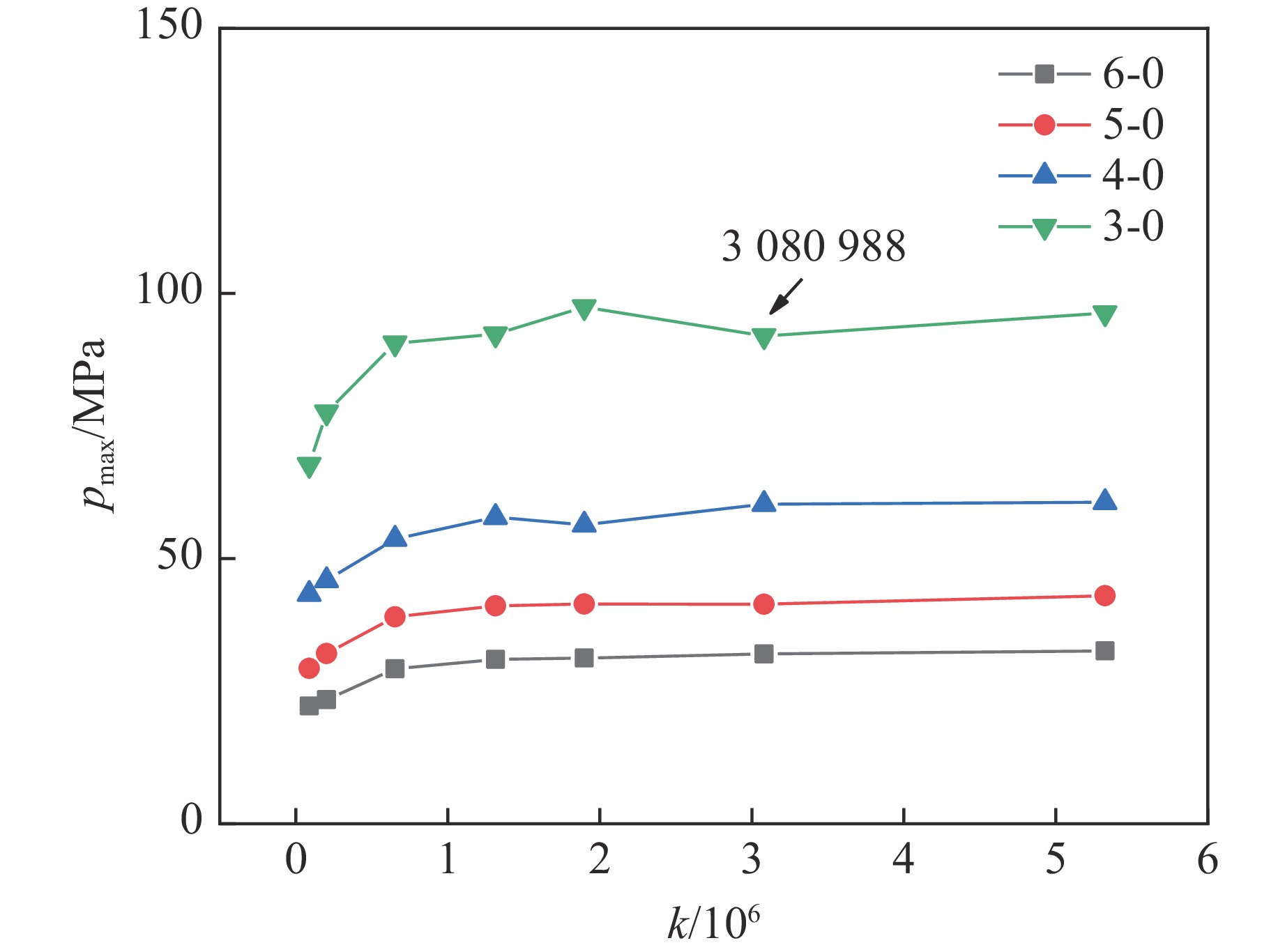
为验证结果的可靠性,对测点3-0、4-0、5-0、6-0测得的冲击波峰值压力进行收敛性分析,得到冲击波峰值压力pmax随网格数量k的变化曲线,如图2所示。当网格数量为3080988时,测点测得的冲击波峰值压力基本收敛。为此,选取网格数量为5324000来研究近海底水下爆炸冲击波的载荷特性。
1.3 数值验证
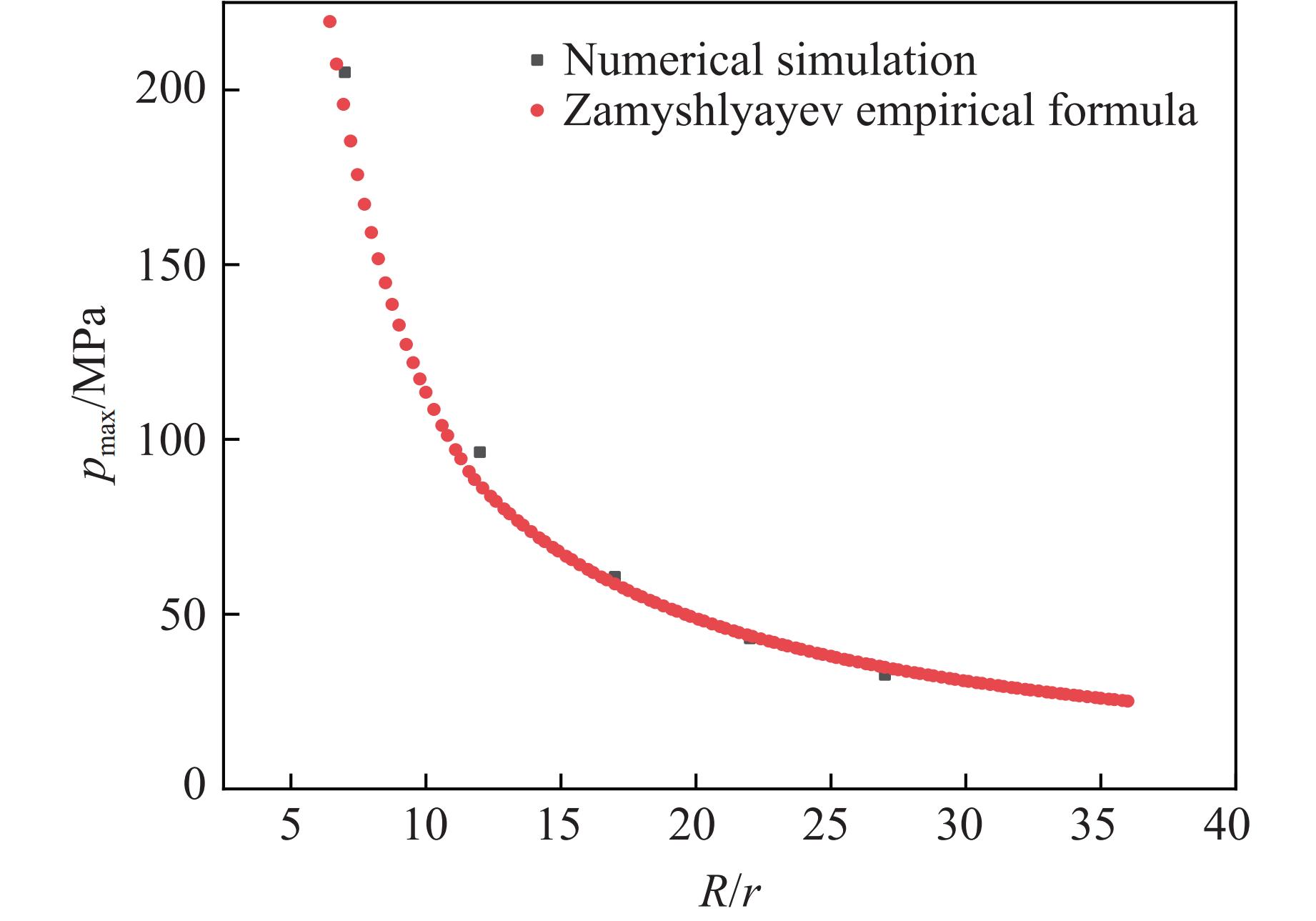
为验证模型的准确性,选取测点2-0、3-0、4-0、5-0、6-0在无海底底质时测得的峰值压力与Zamyshlyayev经验公式计算结果进行对比,如图3和表5所示。可以看出,数值模拟结果与经验公式拟合结果符合得较好,说明该模型能够用于近海底水下爆炸冲击波研究。
表 5 数值模拟与经验公式结果对比Table 5. Comparison of numerical simulation and empirical formula resultsR/r Peak pressure/MPa Error/% Simulation Empirical formula 7 205.03 193.72 5.84 12 96.32 86.90 10.84 17 60.65 58.62 3.45 22 43.04 43.81 1.75 27 32.58 37.91 14.07 1.4 工况设置
为研究水深(H)及海底底质对近海底水下爆炸冲击波载荷特性的影响,仅改变海底底质及静水压力,其他条件保持不变,进行数值模拟,计算工况如表6所示,其中:工况1和工况2用于研究自由场与近海底冲击波压力的差异,工况2和工况3用于研究底质条件对近海底爆炸冲击波载荷特性的影响,工况2、工况4和工况5用于研究水深对近海底水下爆炸冲击波载荷特性的影响。
表 6 数值模拟工况设置Table 6. Settings of simulation casesCase H/m Seafloor sediment Explosive environment 1 50 Nothing Free field 2 50 Model 1 Near the seabed 3 50 Model 2 Near the seabed 4 100 Model 1 Near the seabed 5 150 Model 1 Near the seabed 2. 结果讨论与分析
2.1 自由场和近海底爆炸冲击波特性对比
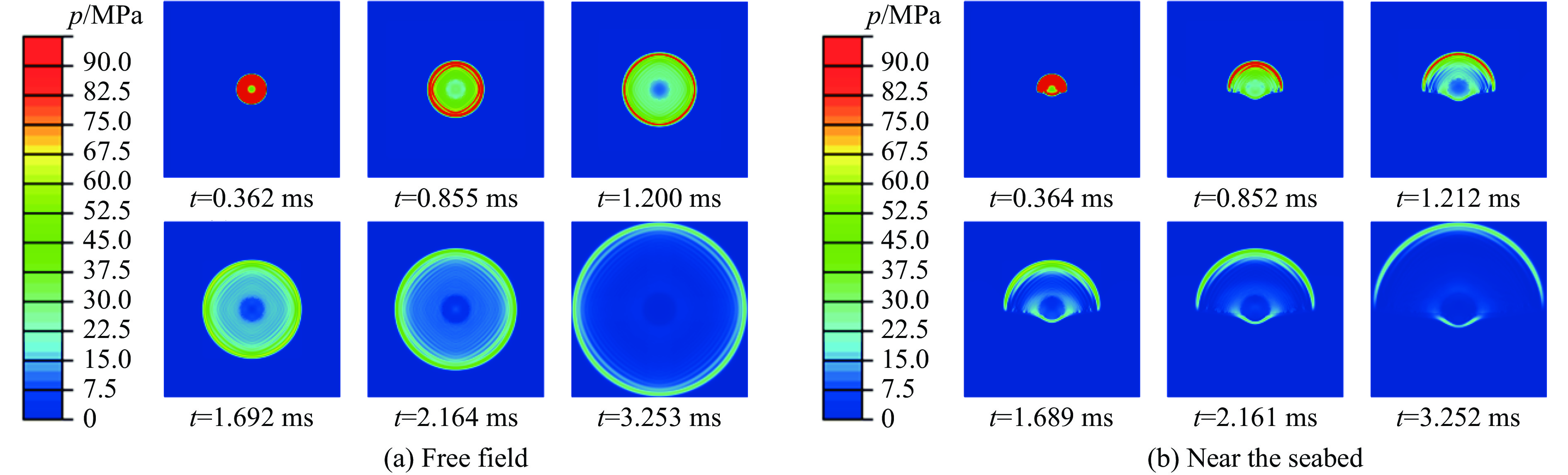
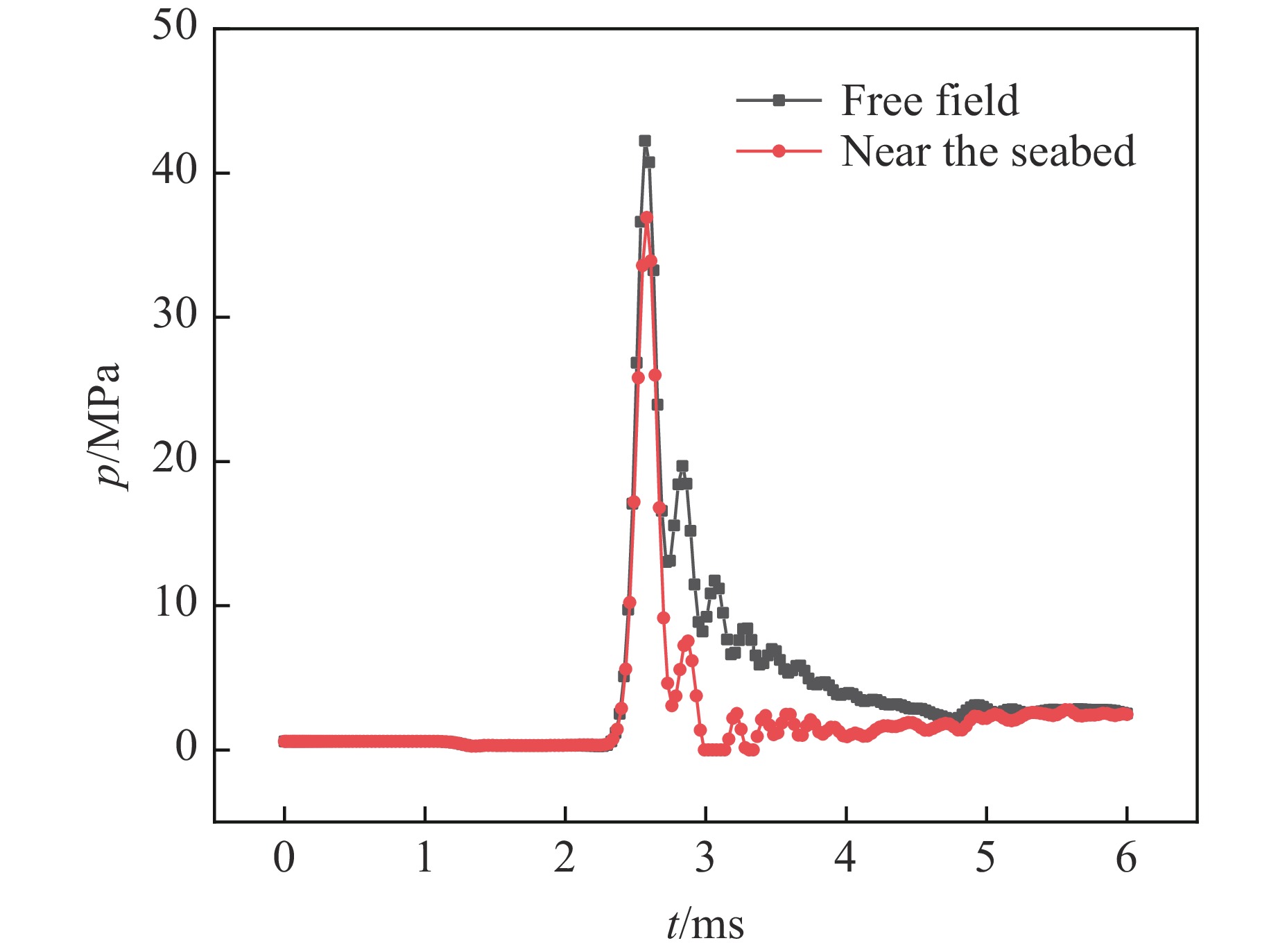
图4为工况1和工况2下不同时刻的冲击波压力云图,图5为测点5-3在工况1和工况2下测得的爆炸冲击波压力时程曲线。可以看出,自由场水下爆炸与近海底水下爆炸存在明显差别,受近海底条件的影响,近海底水下爆炸冲击波形状不是规则的圆形,冲击波波面上的压力峰值并非处处相等,而是越靠近海底区域,冲击波压力越小,测点5-3在近海底条件下测得的冲击波峰值压力及后续的脉动压力均小于自由场条件下测得的压力。由于水的冲击阻抗大于海底底质模型1的冲击阻抗,因此,水中冲击波在近海底的反射波为稀疏波,稀疏波追上冲击波波面将会导致冲击波压力降低;另外,海底底质模型1是一种较软且易变形的底质,冲击波作用在海底底质上,不仅会发生反射,还会发生透射,部分能量传递到海底底质中,使海底底质发生形变,冲击波能量也会发生损耗。因此,在近海底条件下,冲击波峰值压力和气泡脉动压力均小于自由场下的压力,理论与数值模拟结果相符。
近海底水下爆炸时,靠近海底区域处的冲击波压力明显偏小,即不同测点角度(α)条件下的冲击波峰值压力存在差异。定义测点测得的冲击波峰值压力与自由场时的冲击波峰值压力之比为该测点的反射系数。计算所有测点的反射系数,结果如图6所示。当爆距比一定时,随着α的增大,反射系数也逐渐增大,即海底吸能现象和稀疏波的影响逐渐减小;α在0°~10°区间时,海底的吸能现象过于剧烈,故不对该角度范围进行深入研究;当α处于20°~30°区间时,测点的反射系数随爆距比增加呈减小趋势,即近海底反射的影响随爆距比的增大而增强;当α > 40°时,海底吸能现象不明显。
为了更细致地研究近海底反射规律,将自由场与近海底工况下测点2-2~测点2-9、测点3-2~测点3-9、测点4-2~测点4-9的冲击波峰值压力进行对比,结果如表7所示,可以看出:当α处于20°~30°时,近海底工况下,冲击波峰值压力是自由场工况下冲击波峰值压力的81%~91%;随着α的增大,测点距海底越来越远,近海底反射现象也越来越弱,近海底反射影响逐渐消失。
表 7 自由场与近海底测得的冲击波峰值压力对比Table 7. Comparison of peak pressures of free-field and near-seabed underwater explosion shock waveR/r α/(°) pmax/MPa Reflection
coefficientR/r α/(°) pmax/MPa Reflection
coefficientNear seabed Free field Near seabed Free field 7 20 179.29 201.44 0.89 12 60 92.73 95.67 0.97 7 30 186.21 203.80 0.91 12 70 95.00 97.86 0.97 7 40 193.43 204.80 0.94 12 80 98.33 93.98 1.05 7 50 194.98 204.80 0.95 12 90 92.42 96.30 0.96 7 60 192.78 203.80 0.95 17 20 47.78 58.76 0.81 7 70 195.10 201.43 0.97 17 30 53.24 59.25 0.90 7 80 202.46 201.74 1.00 17 40 56.52 58.58 0.96 7 90 196.41 195.79 1.00 17 50 58.40 58.58 1.00 12 20 82.82 97.87 0.85 17 60 59.44 59.27 1.00 12 30 86.62 95.67 0.91 17 70 61.07 60.10 1.02 12 40 93.96 94.66 0.99 17 80 60.00 61.17 0.98 12 50 96.23 94.65 1.02 17 90 57.77 59.91 0.96 2.2 海底底质对近海底爆炸冲击波载荷特性的影响
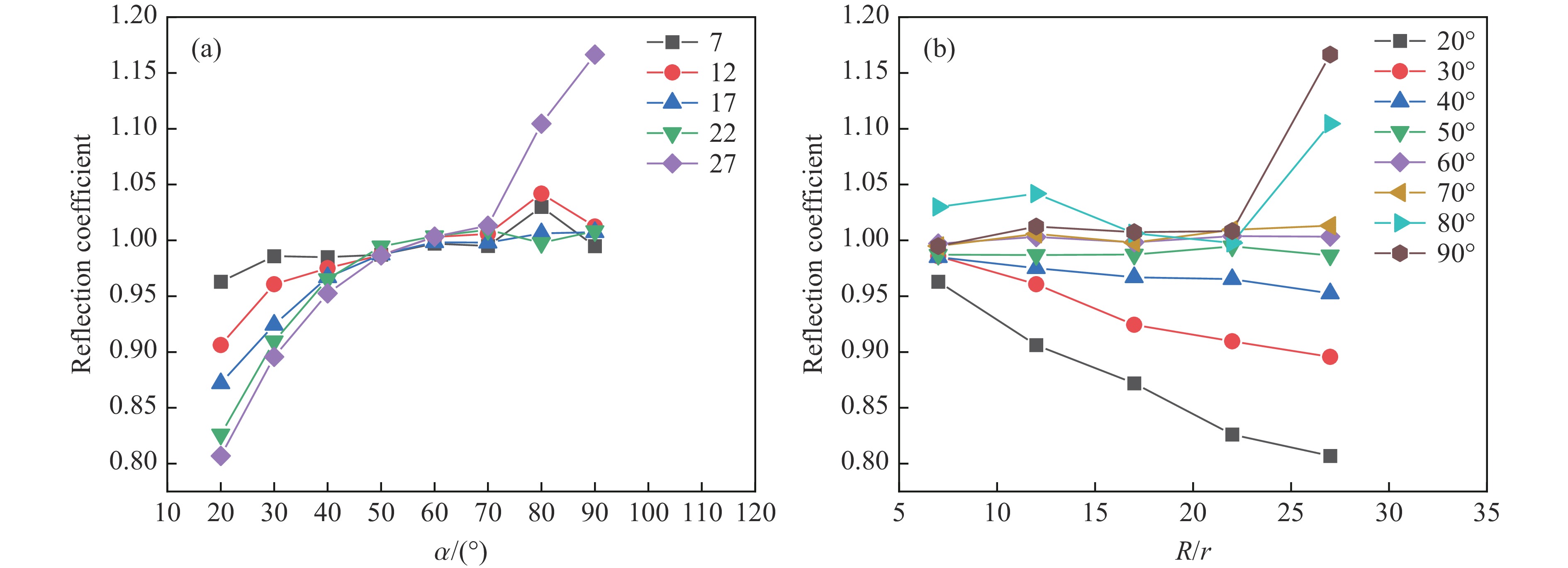
图7显示了工况2和工况3下相同测点测得的近海底冲击波反射系数对比。可以发现,2种底质条件下冲击波传播规律存在明显差异:当底质为模型1时,由于近海底反射波为稀疏波,稀疏波追上冲击波波面将导致冲击波峰值压力变小,且海底底质模型1较软,吸能作用较强,因此,绝大部分测点的反射系数小于1;当海底底质为模型2时,受刚固边界的影响,近海底反射波为压缩波,压缩波追上冲击波波面会导致冲击波峰值压力增大,且海底底质模型2的吸能作用较弱,绝大部分测点的反射系数大于1。无论底质是模型1还是模型2,反射系数异常均发生在爆距比为7~15、α在60°~90°范围内。
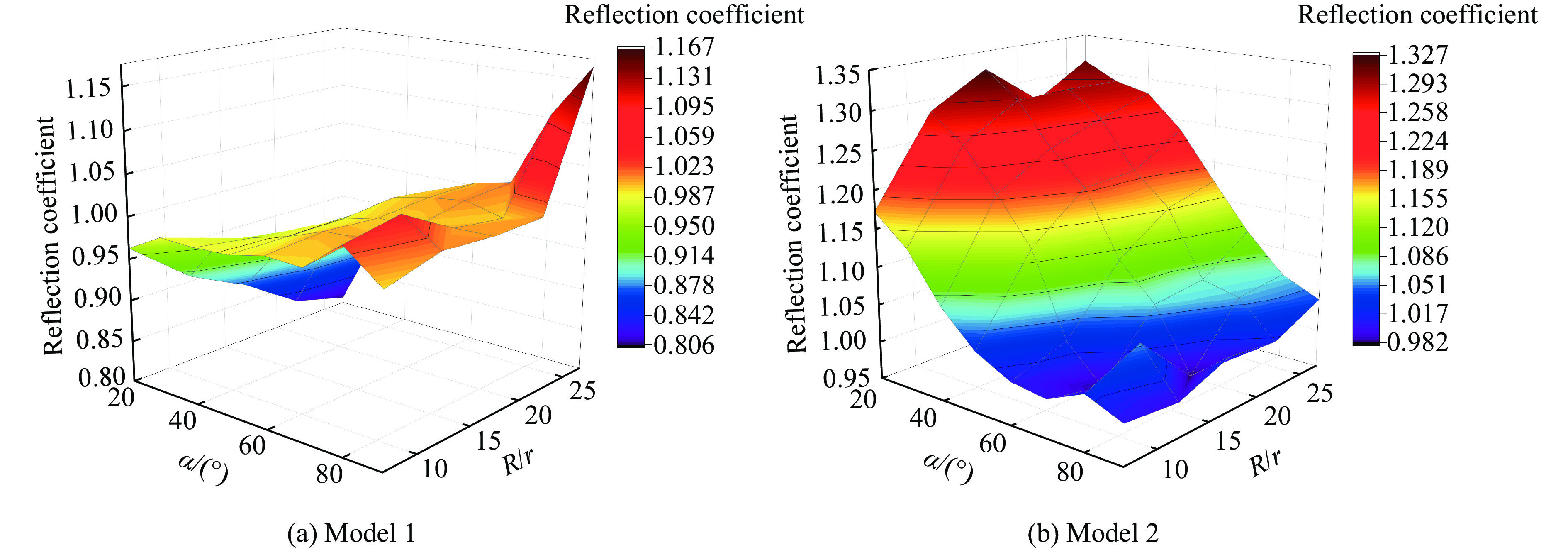
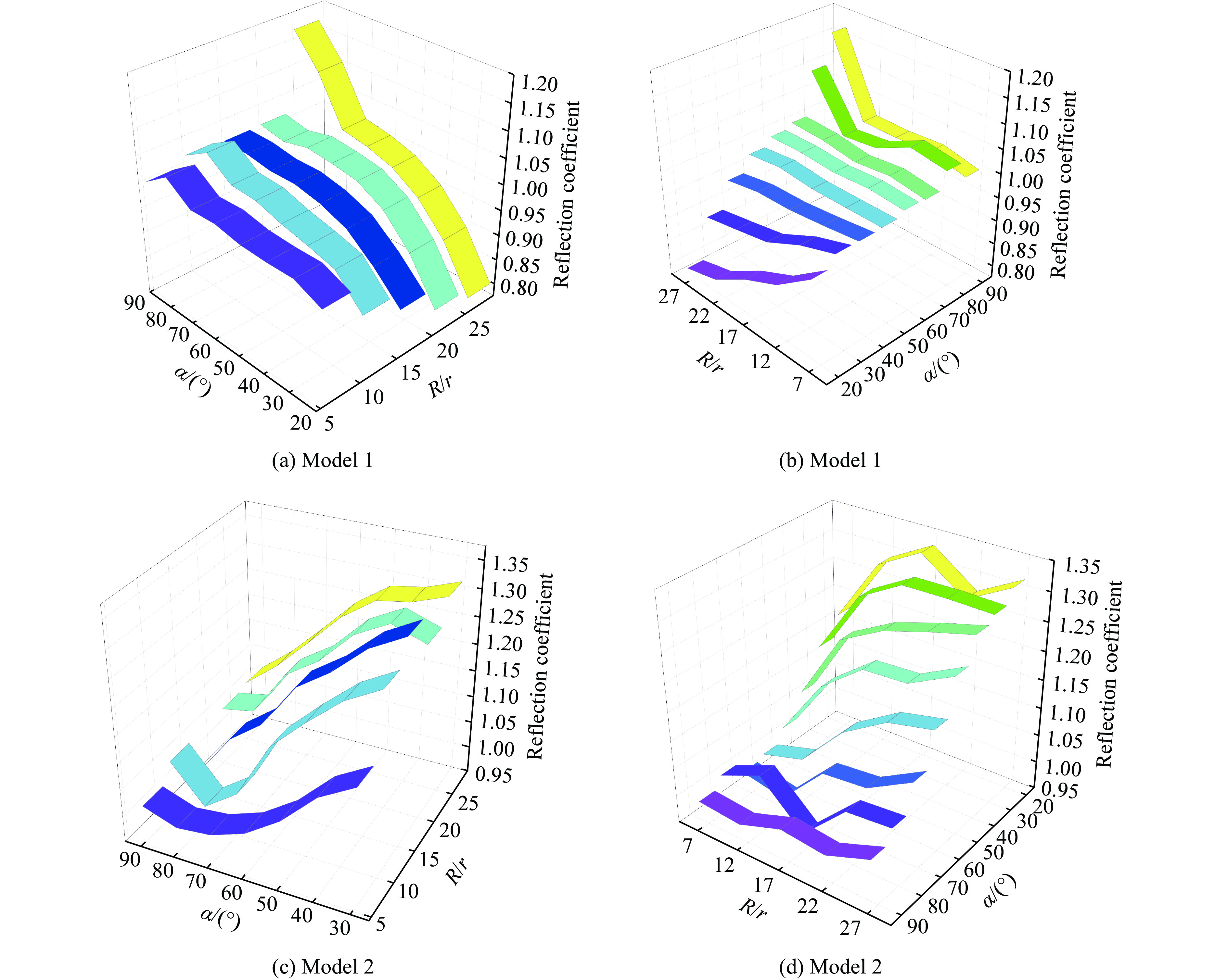
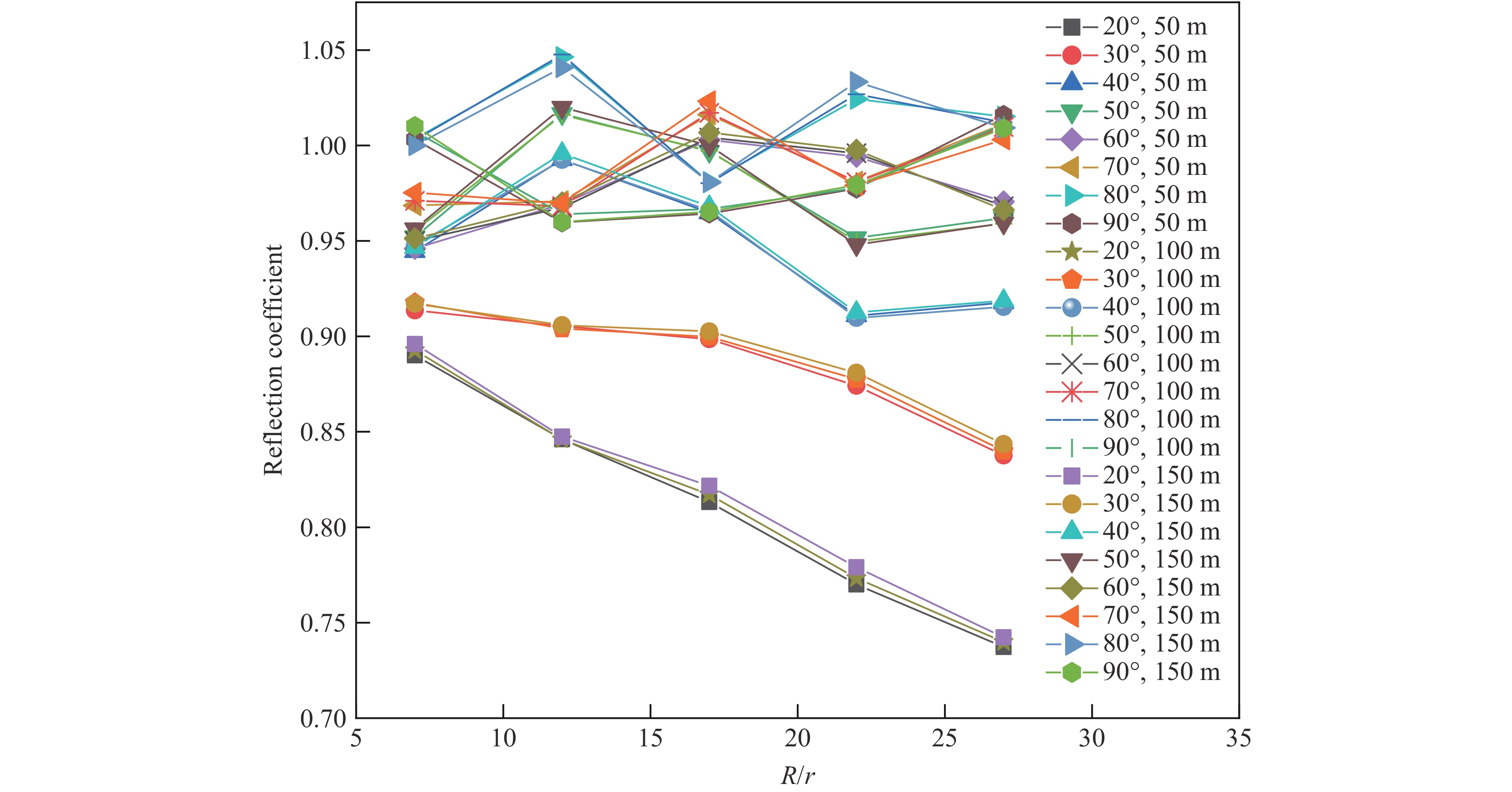
为更清楚地研究不同底质条件对反射系数的影响,将不同底质条件下反射系数随测点角度和爆距比的变化绘制成图8。由图8(a)可知,当海底底质为模型1、爆距比保持不变时,反射系数随测点角度的增大呈增大趋势。由图8(c)可知,当海底底质为模型2、爆距比一定时,反射系数随测点角度的增大呈减小趋势。
当海底底质为模型1时,海底底质较软,海底反射稀疏波,对TNT爆炸冲击波的吸收较强,因此,近海底冲击波峰值压力减小,反射系数小于1是常态。图8(a)显示,当爆距比一定时,测点角度越大,反射系数就越大,因而可以推断,海底底质对不同测点角度处反射系数的影响随测点角度的增大而减弱。当海底底质为模型2时,海底底质较硬,海底反射压缩波,对冲击波的吸收很弱,因此,近海底冲击波峰值压力更大,反射系数大于1是常态。图8(c)显示,当爆距比一定时,测点角度越大,反射系数越小,同样可以得到海底底质对不同测点角度处反射系数的影响随测点角度增大而减弱的结论。
从图8(b)可以看出,当测点角度处于20°~40°区间时,不同测点测得的近海底冲击波反射系数随着爆距比的增大而减小;而图8(d)显示,当测点角度处于20°~60°区间时,不同测点测得的近海底冲击波反射系数随着爆距比的增大而增大。由于2种底质对近海底冲击波反射系数的影响截然相反,因此,综合图8(b)和图8(d)可以看出,测点角度在一定范围内时,海底底质对反射系数的影响随着测点爆距比的增大而增强。当测点角度超出该范围时,该现象减弱甚至消失。综合图8(a)~图8(d)可以发现,虽然海底底质发生了变化,不同海底底质对冲击波的影响效果不同,但是测点反射系数受显著影响的区域均集中在20°~50°范围。
为研究近海底水下爆炸反射波对冲击波的影响是否与起爆深度有关,将底质条件为模型1时不同水深处各测点的反射系数进行对比,结果如图9所示。从图9可以看出,随着水深的增加,同一测点处的反射系数基本一致,说明水深并不能显著影响反射系数,即水深的变化并不会对近海底反射现象造成显著影响,也不会对海底底质的吸能作用造成显著影响,近海底反射稀疏波对冲击波的削减作用并不会随着静水压力的变化而发生显著变化。
3. 结 论
基于CEL方法建立了近海底水下爆炸数值模型,对近海底爆炸冲击波的时空分布规律进行了研究,探究了海底底质和水深对近海底爆炸冲击波载荷特性的影响规律,得到如下结论。
(1) 近海底水下爆炸冲击波载荷特性与自由场明显不同。当测点角度为20°~30°时,近海底反射系数为0.81~0.91;随着测点角度进一步增大,近海底反射的影响逐渐减弱;当测点角度达到80°~90°时,近海底反射的影响基本消失。
(2) 在一定的角度范围内,近海底反射的影响随着爆距比的增大而增强,超出该角度范围后,该现象基本消失。改变底质时,近海底反射的影响使冲击波峰值压力增强或减弱,并且影响区域基本一致。水深对近海底水下爆炸反射系数无显著影响。
(3) 海底底质材料属性不同时,其对爆炸冲击波的吸收作用也存在差异,近海底水下爆炸反射波的种类也不一致。当海底底质较硬时,海底底质对冲击波的吸收作用相对较弱,反射波为压缩波,致使测点角度在20°~50°范围内的冲击波峰值压力增大,当测点角度在20°~50°范围内且测点角度一定时,反射系数随爆距比的增大而增大;当海底底质较软时,海底底质对冲击波的吸收作用较强,近海底反射波为稀疏波,致使20°~50°角度范围内冲击波峰值压力减小,当测点角度在20°~50°范围内且测点角度一定时,反射系数随爆距比的增大而减小。海底底质对反射系数的影响区域主要集中在20°~50°测点范围内,超出该范围时,海底底质对反射系数的影响随着测点角度的增大而逐渐消失,海底底质对反射系数的影响随爆距比的增大而增强的现象也随测点角度的增大而逐渐消失。
-
Table 1. Optimized structural parameters, atomic position parameters for the α-LiAlH4 and the β-LiAlH4 structures
Phase Unit-cell dimensions Atom coordinates α-LiAlH4
(P21/c)a=0.485 1 nm(0.481 7 nm*)
b=0.781 4 nm(0.780 2 nm*)
c=0.773 2 nm(0.782 1 nm*)Li:(0.585, 0.459, 0.829), (0.560, 0.466, 0.827)*
Al:(0.159, 0.204, 0.938), (0.139, 0.203, 0.930)*
H1:(0.193, 0.102, 0.766), (0.183, 0.096, 0.763)*
H2:(0.377, 0.371, 0.986), (0.352, 0.371, 0.975)*
H3:(0.254, 0.082, 0.119), (0.243, 0.081, 0.115)*
H4:(0.822, 0.268, 0.882), (0.799, 0.247, 0.872)*β-LiAlH4
(I2/b)a=0.445 2 nm
b=0.445 9 nm
c=1.010 2 nm
β=89.978°Li:(0, 0.250, 0.125)
Al:(0, 0.250, 0.625)
H1:(0.259, 0.425, 0.542)
H2:(0.324, 0.508, 0.792)Note:"*" represents experimental data from Ref.[18]. Table 2. Average net charges, bond length (L) and scaled bond overlap population (Ps) between H, Al, and Li atoms in the α-LiAlH4 (at 0 GPa) and the β-LiAlH4 (at 2.0 GPa) structures
Phase Average net charge L/nm Ps H Al Li Al─H Li─H Al─H Li─H α-LiAlH4 -0.48 0.64 1.29 0.161 5 0.188 6 0.506 0.019 β-LiAlH4 -0.46 0.55 1.28 0.162 8 0.206 7 0.534 -0.063 -
[1] SCHLAPBACH L, ZÜTTEL A.Hydrogen-storage materials for mobile applications[J]. Nature, 2001, 414(6861):353-358. doi: 10.1038/35104634 [2] SCHÜTH F, BOGDANOVIC' B, FELDERHOFF M.Light metal hydrides and complex hydrides for hydrogen storage[J]. Chemical Communications, 2005, 36(2):2249-2258. [3] ZHU C Y, LIU Y H, DUAN D F.Structural transitions of NaAlH4 under high pressure by first-principles calculations[J]. Physica B:Condensed Matter, 2011, 406(8):1612-1614. doi: 10.1016/j.physb.2011.02.007 [4] DILTS J A, ASHBY E C.Thermal decomposition of complex metal hydrides[J]. Inorganic Chemistry, 1972, 11(6):1230-1236. doi: 10.1021/ic50112a015 [5] DYMOVA T N, ALEKSANDROV D P, KONOPLEV V N, et al.Spontaneous and thermal-decomposition of Lithium Tetrahydroaluminate LiAlH4-the promoting effect of mechanochemical action on the process[J]. Russian Journal of Coordination Chemistry, 1994, 20(4):279-285. http://www.academia.edu/13646109/Hydrogen_production_from_solid_reactions_between_MAlH4_and_NH4Cl [6] VAJEESTON P, RAVINDRAN P, VIDYA R, et al.Huge-pressure-induced volume collapse in LiAlH4 and its implications to hydrogen storage[J]. Physical Review B, 2003, 68:212101. doi: 10.1103/PhysRevB.68.212101 [7] PITT M P, BLANCHARD D, HAUBACK B C, et al.Pressure-induced phase transitions of the LiAlD4 system[J]. Physical Review B, 2005, 72:214113. doi: 10.1103/PhysRevB.72.214113 [8] CHELLAPPA R S, CHANDRA D, GRAMSCH S A, et al.Pressure-induced phase transformations in LiAlH4[J]. The Journal of Physical Chemistry B, 2006, 110(23):11088-11097. doi: 10.1021/jp060473d [9] TALYZIN A V, SUNDQVIST B.Reversible phase transition in LiAlH4 under high-pressure conditions[J]. Physical Review B, 2004, 70:180101. doi: 10.1103/PhysRevB.70.180101 [10] HOHENBERG P, KOHN W.Inhomogeneous electron gas[J]. Physical Review B, 1964, 136(3):864-871. [11] KOHN W, SHAM L.Self-consistent equations including exchange and correlation effects[J]. Physical Review A, 1965, 140(4):1133-1138. http://tu-freiberg.de/sites/default/files/media/institut-fuer-theoretische-physik-10451/Lehre/Dichtefunktionaltheorie/a9rf1a3.pdf [12] PERDEW J P, WANG Y.Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(23):13244-13249. doi: 10.1103/PhysRevB.45.13244 [13] TROULLIER N, MARTINS J L.Efficient pseudopotentials for plane-wave calculations[J]. Physical Review B, 1991, 43(3):1993-2006. doi: 10.1103/PhysRevB.43.1993 [14] SEGALL M D, LINDAN P J D, PROBERT M J, et al.First-principles simulation:ideas, illustrations and the CASTEP code[J]. Journal of Physics:Condensed Matter, 2002, 14:2717-2744. doi: 10.1088/0953-8984/14/11/301 [15] MONKHORST H J, PACK J D.Special points for Brillouin-zone integrations[J]. Physical Review B, 1976, 13(12):5188-5192. doi: 10.1103/PhysRevB.13.5188 [16] PARLINSKI K, LI Z Q, KAWAZOE Y.First-principles determination of the soft mode in cubic ZrO2[J]. Physical Review Letters, 1997, 78(21):4063-4066. doi: 10.1103/PhysRevLett.78.4063 [17] TOGO A, OBA F, TANAKA I.First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures[J]. Physical Review B, 2008, 78(13):134106. doi: 10.1103/PhysRevB.78.134106 [18] HAUBACK B C, BRINKS H W, FJELLVG H.Accurate structure of LiAlD4 studied by combined powder neutron and X-ray diffraction[J]. Journal of Alloys and Compounds, 2002, 346(1):184-189. [19] SEGALL M D, PICKARD C J, SHAH R, et al.Population analysis in plane wave electronic structure calculations[J]. Molecular Physics, 1996, 89(2):571-577. doi: 10.1080/002689796173912 [20] MULLIKEN R S.Electronic population analysis on LCAO-MO molecular wave functions[J]. The Journal of Chemical Physics, 1955, 23(10):1833-1840. doi: 10.1063/1.1740588 [21] HU C H, CHEN D M, WANG Y M, et al.First-principles investigations of the pressure-induced structural transitions in Mg(AlH4)2[J]. Journal of Physics:Condensed Matter, 2007, 19:176205. doi: 10.1088/0953-8984/19/17/176205 [22] WANG H, LI Q, WANG Y C, et al.High-pressure polymorphs of Li2BeH4 predicted by first-principles calculations[J]. Journal of Physics:Condensed Matter, 2009, 21:385405. doi: 10.1088/0953-8984/21/38/385405 -







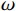
 下载:
下载:
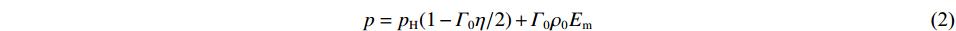
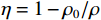
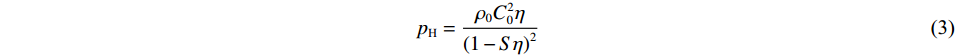
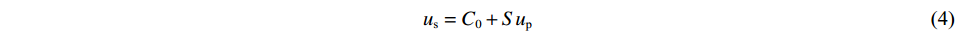
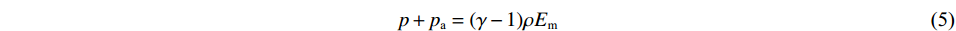
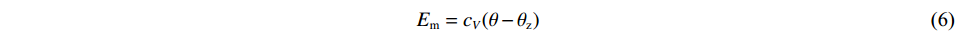
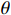
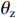










 下载:
下载: