泡沫金属夹芯结构是一种功能与结构一体化的复合结构，由于其具有重量轻、强度高、抗冲击性能好等力学特性，在危险品运输以及高速列车/汽车碰撞、防护领域得到广泛的应用，拥有良好的工程应用前景^[1–2]。

很多学者对金属夹芯结构在冲击荷载下的动态响应问题进行了研究，但大部分研究集中于泡沫金属夹芯结构在单次冲击荷载下的实验、数值模拟以及理论分析。Xiang等^[3]通过实验与理论结合的方法研究了泡沫金属芯夹芯梁在低速冲击下的响应，结果表明，加载位置、几何形状和材料性能对夹芯梁的低速冲击响应有显著影响。Jing等^[4]通过实验与有限元分析研究了分层梯度泡沫金属夹芯梁在低速冲击下的响应，发现对于3种不同芯层结构的夹芯梁，峰值力和最大挠度随冲击能量的增加而增大，两种梯度夹芯梁的抗冲击能力均弱于非梯度单芯夹芯梁。Zhang等^[5]研究了准静态和低速冲击下泡沫金属芯层复合材料夹芯梁的变形破坏，发现夹芯梁在准静态和低速冲击作用下的破坏模式相似，低速冲击破坏荷载高于准静态破坏荷载。Zhao等^[6]研究了泡沫铝夹芯板在低速冲击下的力学特性，结果表明：具有更高刚度的面板结构可以抵抗更强的冲击载荷；在未穿孔情况下，夹芯结构的吸能能力随芯层厚度的增加而下降；穿孔情况下，夹芯结构的吸能能力随芯层厚度的增加而显著提高。敬霖等^[7]和Jing等^[8]系统研究了泡沫夹芯壳在不同等级冲击载荷下的动态响应，实验观测到了结构的典型失效模式，并通过改变前、后面板和芯层厚度对其抗冲击性能进行了参数分析，此外，针对能量守恒和结构变形过程中的移行铰问题，以经典的3阶段理论框架为基础分析了结构的动态响应过程。Zhou等^[9]采用理论、数值模拟和实验相结合的方法对泡沫夹芯板在低速冲击作用下的力学行为进行了系统分析，考虑弯矩与轴力的相互作用，建立了预测冲击力和挠度的理论分析模型，并通过有限元模拟验证了理论预测的准确性，并进一步讨论了芯层分布、冲击位置和芯层厚度对夹芯板冲击行为的影响。

在实际工程应用过程中，夹芯结构不仅会经受单次冲击载荷作用，而且经常遭受重复冲击载荷作用，尤其是在船舶和海洋工程领域，结构会经受如浮冰反复碰撞载荷、波浪重复撞击载荷、舰载机降落等重复冲击载荷^[10–11]。对于泡沫金属夹芯结构在重复冲击载荷下的力学行为，朱凌等^[12]分析了夹芯梁在重复冲击载荷下的动态响应。Guo等^[13–15]和郭开岭^[16]通过实验和数值模拟研究了重复冲击载荷下泡沫金属夹芯梁和夹芯板结构的动态力学行为，分析了低温对泡沫金属夹芯结构重复冲击响应的影响。Liu等^[17]研究了不锈钢-泡沫铝-合金钢夹芯板在单次和多次冲击下的动力学响应、破坏模式和能量吸收，结果表明，增加面板厚度和芯层厚度可以提高夹芯板的承载力和能量吸收，夹芯板在多次冲击下的冲击响应和破坏模式与单次冲击下的冲击响应和破坏模式存在显著差异。

壳体结构是一种具有优良力学性能的空间曲面结构，已有的研究结果表明，壳体结构在抵抗冲击和爆炸荷载方面具有优势^[18–19]。泡沫金属夹芯壳结构兼具泡沫金属夹芯结构的优良力学性能和壳体结构的构型优势，在工程结构中被广泛应用，但是目前对于泡沫金属夹芯壳在重复冲击下的动态响应还缺少相关研究。不同参数的泡沫金属夹芯壳会随着曲率和冲击次数的变化表现出不同的动态响应机制，因此，需重点研究泡沫金属夹芯壳在重复冲击载荷下的动态响应。本研究将利用ABAQUS有限元分析软件模拟泡沫铝夹芯壳在不同重复冲击载荷作用下的变形模式和能量耗散机理，探讨不同曲率半径、前面板与后面板厚度分配、芯层厚度和冲击能量梯度对其抗冲击性能的影响。

1.   有限元数值模拟

1.1   有限元模型

如图1所示，泡沫铝夹芯壳有限元模型由薄壁金属前面板、后面板和泡沫铝芯层3部分组成。前后薄壁金属面板的材料采用低碳钢，泡沫铝芯层采用闭孔泡沫铝。结构沿轴线方向的长度为L，圆周方向的弧长为S，曲率半径为R，前、后面板的厚度h₁=h₂=1.5 mm，泡沫铝芯层的厚度h_c=10 mm。前、后面板采用缩减积分四边形壳单元S4R进行网格划分，泡沫铝芯层和半球形刚性冲头采用缩减积分六面体单元C3DR8划分。基于载荷和结构的对称性，建立了1/4泡沫铝夹芯壳结构的有限元模型，如图2所示。泡沫铝夹芯壳的固支部分采用全约束边界条件，对称边界面设置对称边界条件。由于网格密度对夹芯壳冲击区域的变形和应力情况有明显影响，因此，对泡沫铝夹芯壳模型的中间区域进行网格加密处理，加密区网格尺寸为0.8 mm，非加密区网格尺寸为1.6 mm。泡沫铝夹芯壳的前面板受冲击速度为v、直径为15 mm的刚性冲头冲击。

图  1  泡沫铝夹芯壳示意图

Figure  1.  Schematic diagram of aluminum foam sandwich shell

下载: 全尺寸图片 幻灯片

图  2  泡沫铝夹芯壳的1/4有限元模型

Figure  2.  Finite element model of 1/4 aluminum foam sandwich shell

下载: 全尺寸图片 幻灯片

将刚性冲头与泡沫铝夹芯壳的前面板之间定义为面面接触，设冲头与前面板之间无摩擦。泡沫铝芯层与前、后面板之间采用绑定（tie）方式连接。利用ABAQUS有限元软件中的重启动技术实现刚性冲头对泡沫铝夹芯壳结构的重复冲击过程。每次冲击结束试件挠度保持稳定后，对刚性冲头重新赋予初始速度v，进行下一次冲击。在重复冲击数值模拟过程中，每次冲击后有限元模型的变形、应力-应变等信息均储存在相应的结果文件中。将上一次冲击的结果作为下一次冲击的初始状态导入，载荷/边界条件保持不变，然后进行下一次冲击模拟。

1.2   材料属性

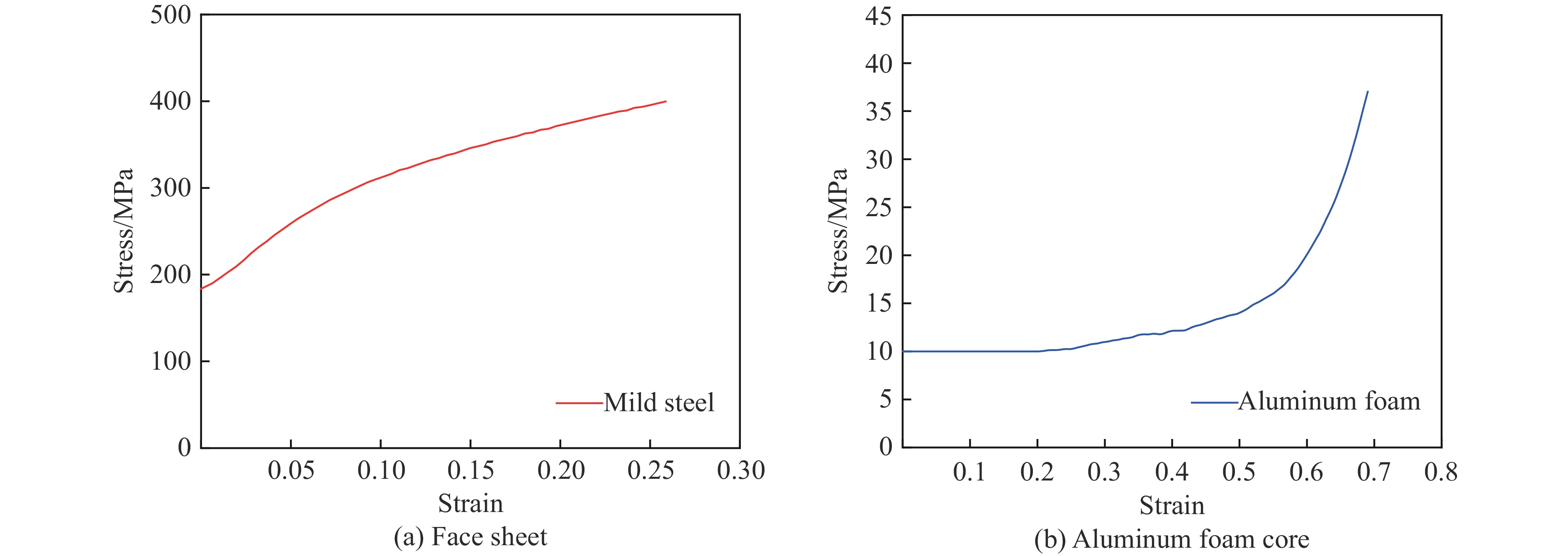
通过万能试验机进行准静态压缩和拉伸试验，获得用于制备泡沫铝夹芯壳的芯层和前、后面板的性能^[15]。在有限元数值模拟中，半球形冲头设置为刚体，前后低碳钢面板用弹塑性强化模型描述，图3(a)给出了面板的塑性应力-应变曲线。采用Deshpande和Fleck^[20]的Crushable Foam模型对泡沫铝芯层进行建模，闭孔泡沫铝芯层的塑性应力-应变曲线如图3(b)所示。面板和芯层的材料参数分别由表1和表2给出。通过数值模拟研究了3种不同曲率的泡沫铝夹芯壳结构，泡沫铝芯层的相对密度均为18.5%。低速冲击作用下前、后面板的应变率效应采用Cowper-Symonds模型^[21]计算

图  3  面板和芯层的应力-应变曲线^[15]

Figure  3.  Stress-strain curves of the face sheet and the foam core^[15]

下载: 全尺寸图片 幻灯片

表  1  面板的材料参数

Table  1.  Material parameters of face sheet

Material	Density/(kg·m−3)	Young modulus/GPa	Yield stress/MPa	Poisson’s ratio
Mild steel	7800	210	182	0.3

下载: 导出CSV 

| 显示表格

表  2  泡沫铝芯层的材料参数

Table  2.  Material parameters of aluminum foam core

Material	Relative density/ %	Young’s modulus/ GPa	Plateau stress/ MPa	Elastic Poisson’s ratio	Plastic Poisson’s ratio	Plastic stress ratio
Aluminum foam	18.5	0.8	10	0.2	0	1.73

下载: 导出CSV 

| 显示表格

式中：${\sigma _{\mathrm{d}}}$为动态屈服应力；${\sigma _{\mathrm{y}}}$为静态屈服应力；$\dot \varepsilon$为材料的应变率；D和P为材料常数，对于钢材，通常取D=6844 s⁻¹， P=3.91。

1.3   有限元模型验证

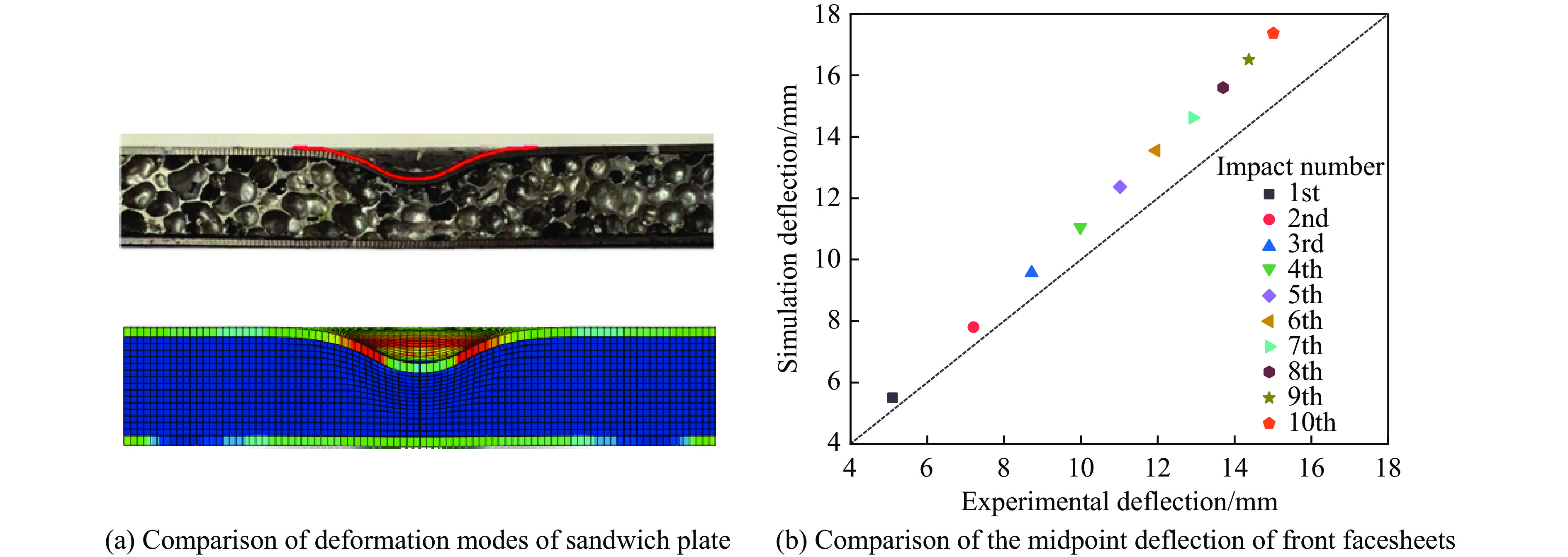
为了验证建立的有限元模型的可靠性及合理性，与文献[16]中的重复冲击实验结果进行对比。泡沫金属夹芯板试件的长和宽均为150 mm，冲击区域的面积为90 mm×90 mm，前、后面板厚度均为1.5 mm，泡沫铝芯层的厚度为15 mm。冲头质量为8.029 kg，冲击速度为3.668 m/s，冲击能量为54 J。数值模拟了重复冲击10次下泡沫铝夹芯板的变形过程，并给出了每次冲击后前面板的中点挠度，如图4所示。图4(a)为泡沫铝夹芯板变形模式的数值模拟与实验结果对比，可以看出，数值模拟与实验结果吻合较好。在冲击荷载作用下，夹芯板前面板产生局部凹陷，冲击区域芯层被压缩，后面板产生较小的整体弯曲变形。图4(b)给出了每次冲击后前面板中点挠度数值模拟与实验结果对比，所得数据点均分布在45°斜线上方，说明数值模拟所得前面板中点的挠度与实验结果较为吻合，该有限元模型可用于后续的数值模拟分析。

图  4  数值模拟可行性分析

Figure  4.  Feasibility analysis of the numerical simulation

下载: 全尺寸图片 幻灯片

2.   数值模拟结果与分析

以曲率半径R为100 mm的泡沫铝夹芯壳（R100）为研究对象，分析其在重复冲击载荷作用下的动态响应。前、后面板厚度h₁=h₂=1.5 mm，泡沫铝芯层厚度h_c=10 mm，夹芯壳沿轴向长度L=100 mm，圆心角α=54°，外弧长S=100.4 mm。有限元模型如图2所示，冲头与前面板之间无摩擦，芯层与前、后面板采用绑定方式连接。每次冲击中，刚性冲头的质量均为5.6 kg，冲击速度为2.535 m/s，作用在结构上的冲击能量为18 J。重复冲击5次，分析每次冲击载荷作用下结构的抗冲击性能、冲击力作用规律和加卸载过程。

结构的能量吸收评价指标主要包括总吸能（E_T）和比吸能（E_SA）。整个变形过程中结构吸收的总能量$E_{\mathrm{T}}$可通过载荷-位移曲线积分获得

式中：F为作用在结构上的瞬时冲击载荷，δ为结构的位移。比吸能E_SA为结构单位质量吸收的能量，可以评估结构的能量吸收能力

式中：m为结构的质量。

2.1   变形模式和能量吸收机理

图5给出了泡沫铝夹芯壳结构在18 J重复冲击载荷下每次冲击后前、后面板与泡沫铝芯层的变形模态。可以看出，前面板受冲头冲击产生明显的局部塑性变形，芯层在冲头冲击位置发生局部压缩，后面板受前面板和芯层的共同作用发生整体弯曲。前3次冲击芯层未达到密实化阶段，泡沫铝夹芯壳结构的变形模式以局部凹陷为主。随着芯层逐渐达到密实化，结构的变形模式以整体弯曲变形为主。前面板在冲击区域两侧形成了塑性铰；后面板的中心变形区域形成了塑性区，塑性区随冲击次数的增加不断扩大。

图  5  R100夹芯壳在重复冲击下的变形模式

Figure  5.  Deformation of R100 sandwich shell under repeated impact

下载: 全尺寸图片 幻灯片

图6为泡沫铝夹芯壳结构前、后面板的中点挠度时程曲线。由图6可知，随着冲击次数的增加，前、后面板的挠度增大。前面板挠度增长速率逐渐减小，后面板挠度增长速率先增大之后逐渐减小。图7为泡沫铝夹芯壳前、后面板和芯层在响应过程中的能量吸收曲线。冲击次数的增加使泡沫铝夹芯壳结构的能量吸收逐渐增大。随着芯层的密实化，结构整体的能量吸收能力降低，每次冲击的能量吸收量逐渐减小。在重复冲击过程中，前面板和芯层吸收了大部分能量。随着冲击次数的增加，结构的前面板和芯层吸能比例逐渐降低，后面板吸能比例逐渐增高。在前3次冲击时，前面板的能量吸收占比较高；直到第4次重复冲击时，前面板和芯层的能量吸收占比近似相等；最后1次冲击之后芯层的能量吸收占比超过了前面板。

图  6  R100夹芯壳前、后面板中点挠度时程曲线

Figure  6.  Midpoint deflection-time curves of front and back face sheet of R100 sandwich shell

下载: 全尺寸图片 幻灯片

图  7  R100夹芯壳重复冲击能量时程曲线

Figure  7.  Energy-time curves of R100 sandwich shell under repeated impact

下载: 全尺寸图片 幻灯片

每次冲击中，当夹芯壳前、后面板中点挠度达到稳定时，其能量吸收达到峰值。冲头产生的动能以变形能的形式被泡沫铝夹芯壳吸收。夹芯壳中存储的变形能可以分为弹性变形能和塑性变形能，之后夹芯壳中存储的弹性变形能被释放，全部转化为冲头的回弹动能，塑性变形能被保留下来。因此，位移和能量时程曲线出现了一个回弹下降阶段，直至稳定下来，在小范围内波动。

2.2   冲击力作用规律和加卸载过程

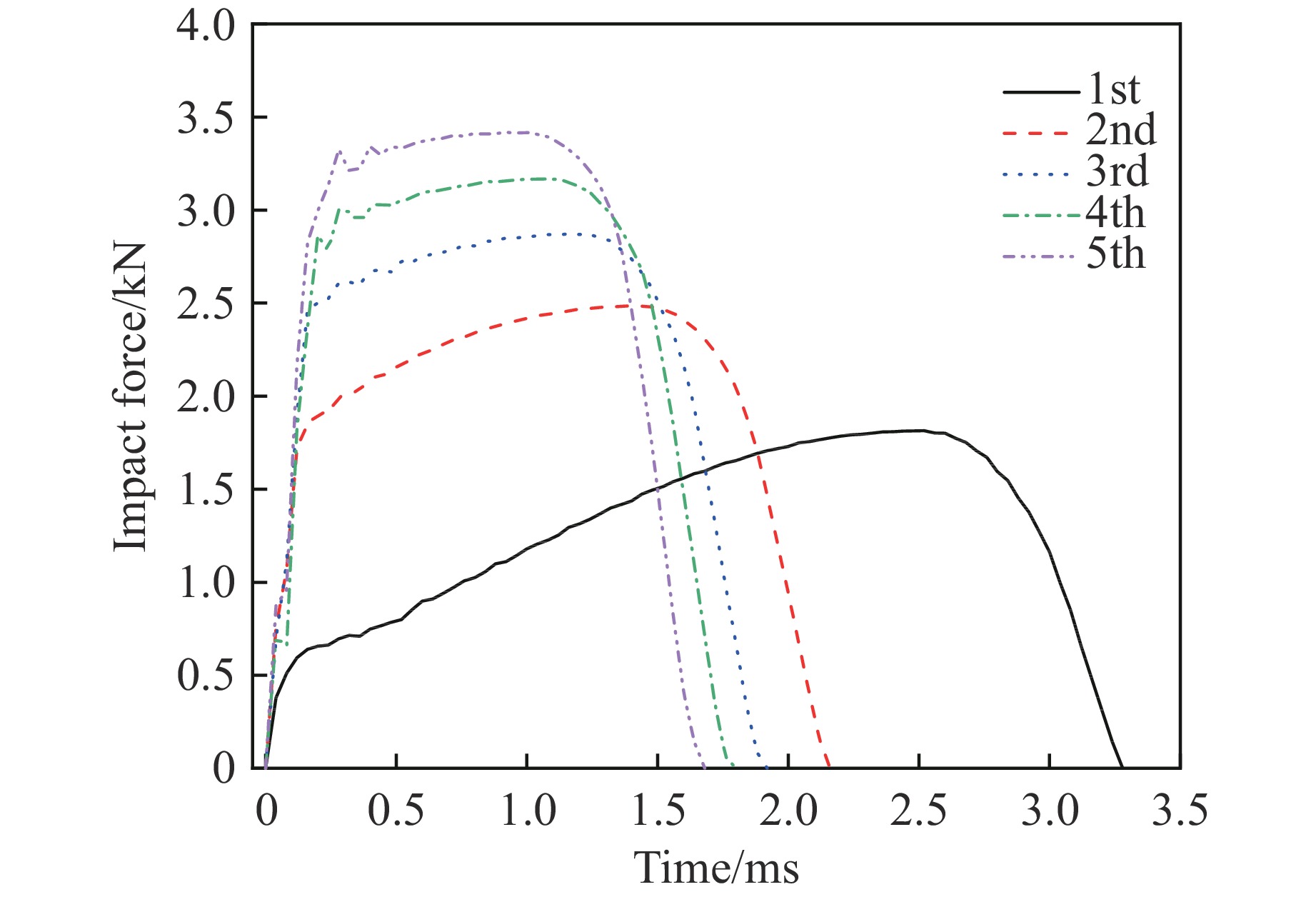
图8给出了R100泡沫铝夹芯壳结构在冲击能量为18 J、5次重复冲击载荷作用下的冲击力时程曲线。可以看出，随着冲击次数的增加，泡沫铝夹芯壳结构弯曲变形逐渐积累，结构整体抗弯刚度增大，冲击力峰值增大，但冲击持续的时间逐渐缩短。泡沫铝夹芯壳结构在重复冲击载荷作用下的冲击力随位移的变化规律如图9所示。从5次重复冲击载荷作用下泡沫铝夹芯壳结构的加载与卸载过程可以看出，结构的冲击过程可分为弹性阶段、塑性强化阶段和弹性卸载阶段3部分，结构的塑性强化随着冲击次数的增加而减弱。

图  8  R100夹芯壳的冲击力时程曲线

Figure  8.  Impact force time curves of R100 sandwich shell

下载: 全尺寸图片 幻灯片

图  9  R100夹芯壳的冲击力-位移曲线

Figure  9.  Impact force-displacement curves of R100 sandwich shell under repeated impact

下载: 全尺寸图片 幻灯片

3.   参数分析

3.1   曲率半径的影响

建立了曲率半径分别为50、100、200 mm 的3种泡沫铝夹芯壳结构，分别记为R50、R100、R200。3种曲率的泡沫铝夹芯壳模型的圆心角α、外弧长S和质量m等数据见表3。为保证3种泡沫铝夹芯壳结构的承载面积相同，沿轴线方向的长度L均取100 mm，根据不同的曲率调整圆心角，从而保证弧长S和边长L近似相等。

表  3  夹芯壳模型的几何参数

Table  3.  Geometric parameters of sandwich shell model

Specimen	R/mm	α/(°)	L/mm	S/mm	m/g
R50	50	104	100	102.5	258.6
R100	100	54	100	100.4	268.5
R200	200	28	100	100.9	278.4

下载: 导出CSV 

| 显示表格

图10为3种曲率的泡沫铝夹芯壳在18 J冲击能量下重复冲击5次时前、后面板中点挠度对比。可以看出，在重复冲击过程中，前、后面板的挠度不断累积，后面板的挠度小于前面板。在本研究的能量等级和曲率半径范围内，单次冲击下曲率半径小的结构抗冲击性更好。随着曲率半径的减小，单次冲击下夹芯壳结构的前面板中点挠度增大，后面板中点挠度减小。

图  10  3种曲率夹芯壳在18 J能量重复冲击下的中点挠度

Figure  10.  Midpoint deflection of three sandwich shells with different curvatures under repeated impact of 18 J energy

下载: 全尺寸图片 幻灯片

重复冲击载荷作用下，曲率半径越小的结构，其前面板中点挠度越大，中点挠度大小随冲击次数的增加始终保持不变。这与刚性冲头压入区域的大小和深度有关，曲率半径越小的夹芯壳结构的初始弯曲程度越大，刚性冲头与结构的接触面积越小，同等冲击能量下结构的塑性变形区域面积小但是深度大，即前面板中点挠度增大。不同曲率的泡沫铝夹芯壳在重复冲击下后面板中点挠度的变化分为3个阶段：第1次和第2次冲击时，R50结构后面板中点的挠度较小；第3次冲击时，R200结构后面板中点的挠度较小，而R100结构后面板中点的挠度较大；随着冲击次数的增加，曲率半径越大，结构后面板中点挠度越小。出现这种规律的原因是曲率半径较小的结构在第3次冲击时芯层的主要受载部分（冲头冲击区域）接近密实化，导致芯层的能量吸收能力下降，结构已经近似于整体板。曲率半径越大的结构，刚性冲头与前面板均接触面积越大，结构以整体弯曲来抵抗冲击载荷，使后面板变形增量变小，在第3次冲击之后表现出较小的后面板中点挠度。因此，曲率半径越大的夹芯壳结构在重复冲击下前、后面板的中点挠度越小，结构的抗重复冲击性能越好。

图11为3种曲率泡沫铝夹芯壳结构在能量为18 J、5次重复冲击载荷作用下结构的比吸能对比。可以看出，第1次冲击时，3种曲率泡沫铝夹芯壳结构的比吸能差异很小，后面板的吸能占比较小。随着冲击次数增加，曲率对结构比吸能的影响逐渐显著，同时后面板的吸能占比增大。随着泡沫铝夹芯壳结构曲率半径的减小，在重复冲击载荷作用下，结构的比吸能增大。从泡沫铝夹芯壳结构各组成部分的能量吸收大小和吸能占比可知，3种曲率泡沫铝夹芯壳的前面板比吸能差异较小，后面板和芯层比吸能差异较大。夹芯壳结构的曲率半径越小，前面板吸能占比越小，后面板和芯层吸能占比越大。这是由于不同曲率夹芯壳的变形模式不同，曲率半径小的夹芯壳结构变形区域面积小但是深度大，冲击中心区域芯层密实化速率快，后面板中心区域弯曲变形大，因此芯层和后面板吸能占比增加。

图  11  3种曲率夹芯壳在18 J能量重复冲击下的比吸能

Figure  11.  Specific energy absorption of three sandwich shells with different curvatures under repeated impact of 18 J energy

下载: 全尺寸图片 幻灯片

3.2   面板厚度的影响

在保持前、后面板总厚度不变的情况下，对芯层厚度为10 mm，不同前、后面板厚度（1.0、1.5、2.0 mm）组合的R50结构进行建模，具体参数见表4。对3种不同厚度分配面板的泡沫铝夹芯壳进行了5次重复冲击，冲击能量均为18 J，分析面板厚度对泡沫铝夹芯壳抗冲击性能和能量吸收的影响。

表  4  不同前、后面板厚度夹芯壳的几何参数

Table  4.  Geometric parameters of different thickness of front and back face of sandwich shell

Specimen	h1/mm	h2/mm	C/mm	m/g
H1	1.0	2.0	10	250.8
H2	1.5	1.5	10	258.6
H3	2.0	1.0	10	266.4

下载: 导出CSV 

| 显示表格

图12为不同壁厚的前、后面板中点挠度随冲击次数的变化曲线。从图12(a)中可以看出，随着冲击次数的增加，前面板中点挠度不断增大，但增大速率不断减小。在给定的冲击能量下，前面板厚度越大，后面板中点挠度越小，并且随着冲击次数的增加，前面板中点挠度的变化规律保持一致。

图  12  3种面板厚度R50夹芯壳在18 J能量重复冲击下的中点挠度

Figure  12.  Midpoint deflection of three R50 sandwich shells with different panel thicknesses under repeated impact of 18 J energy

下载: 全尺寸图片 幻灯片

如图12(b)所示，后面板中点挠度在不同阶段的增长速率不同，前3次冲击的中点挠度增加速率逐渐增大，随后逐渐减小。对于第1次冲击而言，3组不同厚度分配情况下的夹芯壳结构后面板中点挠度相差很小，原因是冲头的冲击能量主要转化为前面板及泡沫金属芯层的塑性变形能。随着冲击次数的增加，芯层逐渐达到密实化，其能量吸收能力显著下降，此时大部分冲击能量都转化为前面板和后面板的塑性变形能。同等冲击能量作用下，后面板中点挠度越小，表明夹芯壳结构的抗冲击性能越好。综上所述，前、后面板总厚度保持不变的情况下，前面板厚度越大，前、后面板的中点挠度越小，夹芯壳结构的抗重复冲击性能越好。

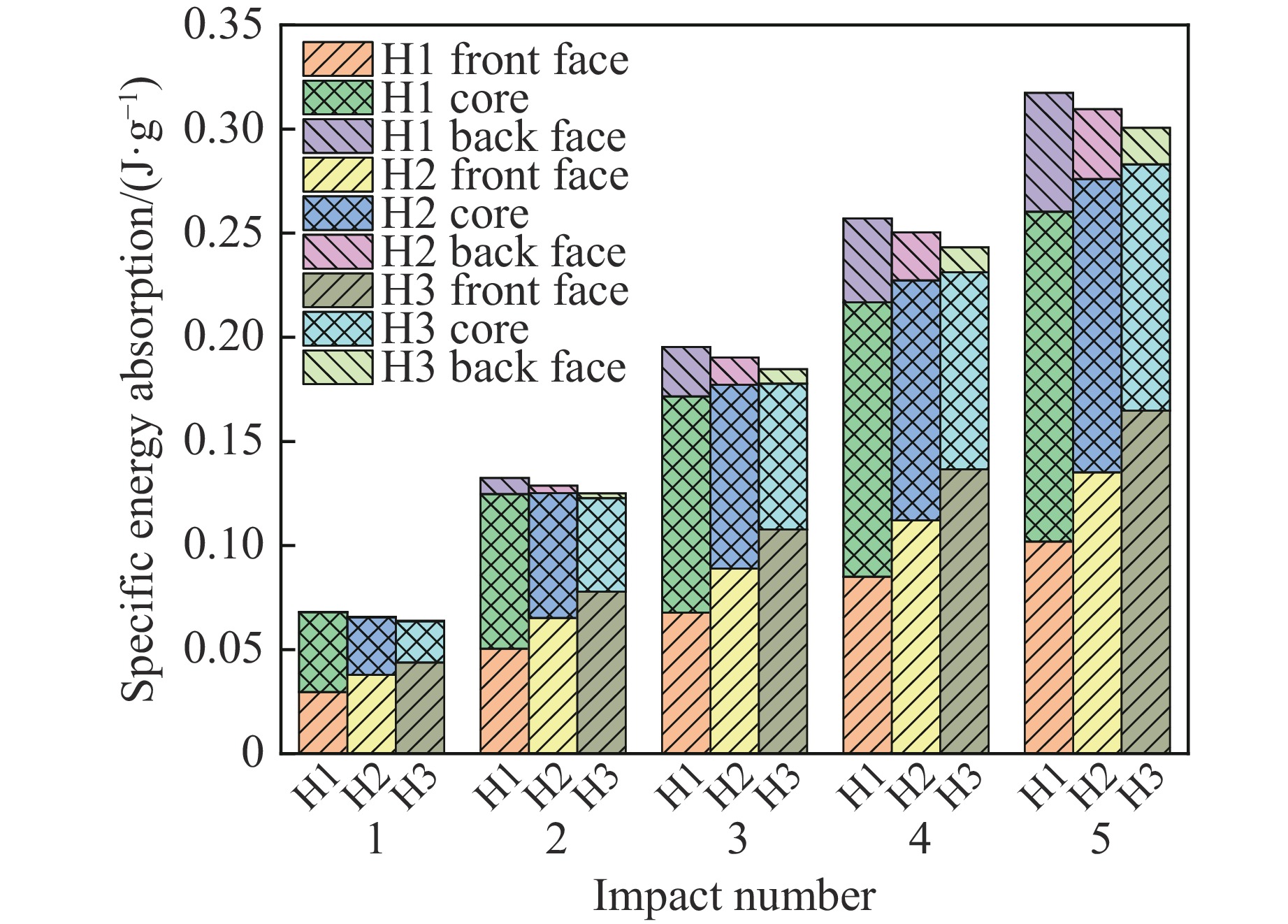
图13为3种不同厚度分配面板的夹芯壳结构重复冲击5次后各组成部分的比吸能。由图13可知，随着冲击次数的增加，泡沫铝夹芯壳的比吸能不断增加，其增长速率不断减小。夹芯壳结构前面板和芯层吸收了大部分能量，后面板吸收的能量较少。试件H1的比吸能大于试件H2和H3，表明前面板厚度越小，结构的比吸能越大。3种不同厚度分配面板的夹芯壳结构的前、后面板以及芯层的能量吸收情况出现较大的差异。试件H3前面板的比吸能高于试件H1和H2，而后面板吸收的能量小于试件H1和H2，表明前面板越厚，前面板吸收的能量越多，后面板吸收的能量越少。对于芯层而言，试件H1芯层的比吸能大于试件H2和H3，表明前面板越薄的结构芯层吸能越多。随着冲击次数的增加，不同工况下前、后面板比吸能差异逐渐增大，而泡沫铝芯层的比吸能差异变化不明显，其原因是在多次冲击之后，泡沫金属芯层达到密实化，能量吸收能力减小，在后续冲击中，3种面板厚度分配的夹芯壳结构中，芯层吸收能量的差值基本保持不变。

图  13  3种面板厚度R50夹芯壳在18 J能量重复冲击下的比吸能

Figure  13.  Specific energy absorption of R50 sandwich shells with three panel thicknesses under repeated impact of 18 J energy

下载: 全尺寸图片 幻灯片

3.3   芯层厚度的影响

在R50泡沫铝夹芯壳结构中，保持前、后面板厚度为1.5 mm不变，对芯层厚度分别为10、15和20 mm的夹芯壳结构进行建模，记为C10、C15和C20，具体参数见表5。对3种芯层厚度的泡沫铝夹芯壳结构进行5次重复冲击，每次冲击能量为18 J，研究芯层厚度对泡沫铝夹芯壳的抗冲击性能和能量吸收的影响。

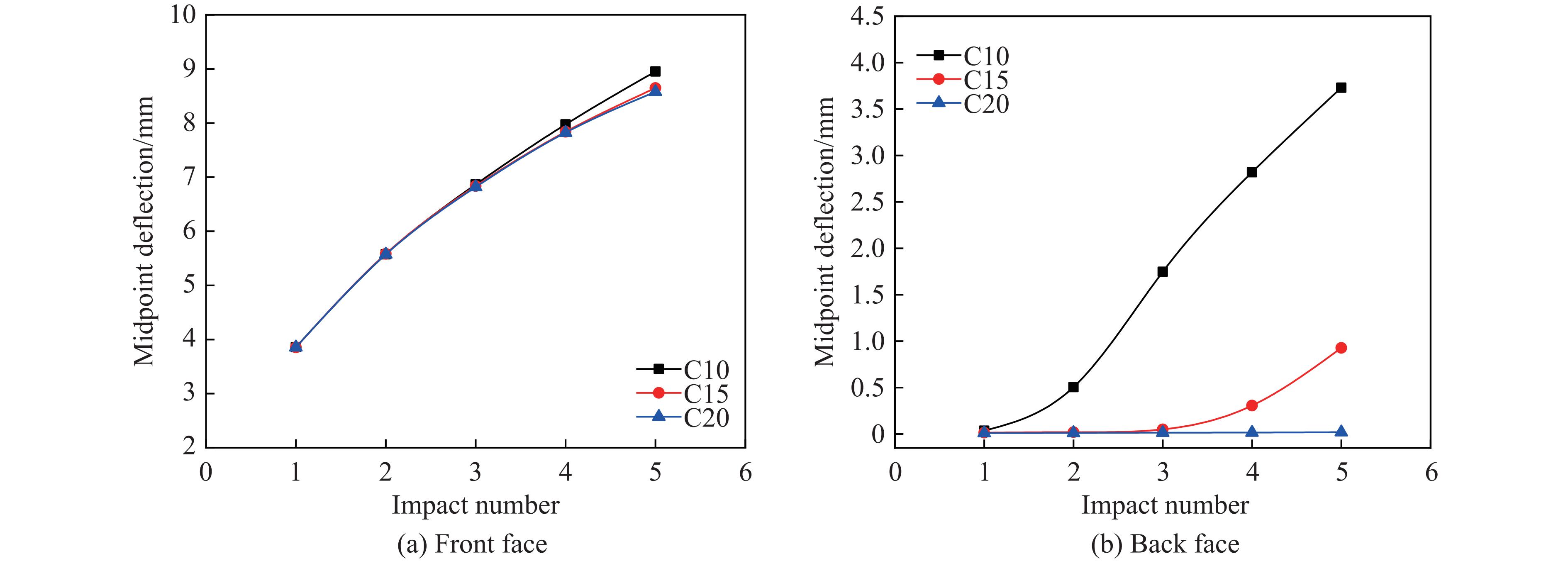
表  5  不同芯层厚度夹芯壳的几何参数

Table  5.  Geometric parameters of sandwich shells with different core thicknesses

Specimen	h1/mm	h2/mm	hc/mm	m/g
C10	1.5	1.5	10	258.6
C15	1.5	1.5	15	281.2
C20	1.5	1.5	20	304.0

下载: 导出CSV 

| 显示表格

图14显示了3种芯层厚度的夹芯壳结构前、后面板中点挠度随冲击次数的变化。不同芯层厚度的试件对重复冲击荷载的抵抗能力不同，随着冲击次数的增加，前面板的中点挠度不断增大，但增速不断减小。当冲击能量一定时，芯层越厚，每次冲击后前面板的中点挠度越小，并且随着冲击次数的增加，不同芯层厚度夹芯壳结构的前面板中点挠度的差异逐渐变大。

图  14  3种芯层厚度R50夹芯壳在18 J能量重复冲击下的中点挠度

Figure  14.  Midpoint deflection of three R50 sandwich shells with different core thickness under repeated impact of 18 J energy

下载: 全尺寸图片 幻灯片

在重复冲击荷载作用下，不同芯层厚度的夹芯壳结构后面板中点挠度的增长速率不同，芯层越薄，后面板的中点挠度增长越快。试件C10的后面板挠度增长速率明显高于C15和C20，且随着冲击次数的增加，后面板中点挠度差异逐渐增大。C10后面板中点挠度的增长速率先增大后减小，试件C15在前3次冲击时的后面板中点挠度增量较小，后2次逐渐增大。试件C20后面板的中点挠度在5次冲击过程中保持不变。第1次冲击时，3种芯层厚度的夹芯壳结构的后面板挠度近似相等，冲击能量主要转化为前面板及芯层的塑性变形能。在后续冲击中，由于泡沫金属芯层逐渐达到密实化，芯层较薄结构的能量吸收能力明显下降，大部分冲击能量都转化为前面板和后面板的塑性变形能。芯层越厚，芯层密实化所需的冲击次数越多，后面板的中点挠度越小。在曲率和面板厚度不变的情况下，芯层越厚，前、后面板的中点挠度越小，夹芯壳的抗重复冲击性能越好。

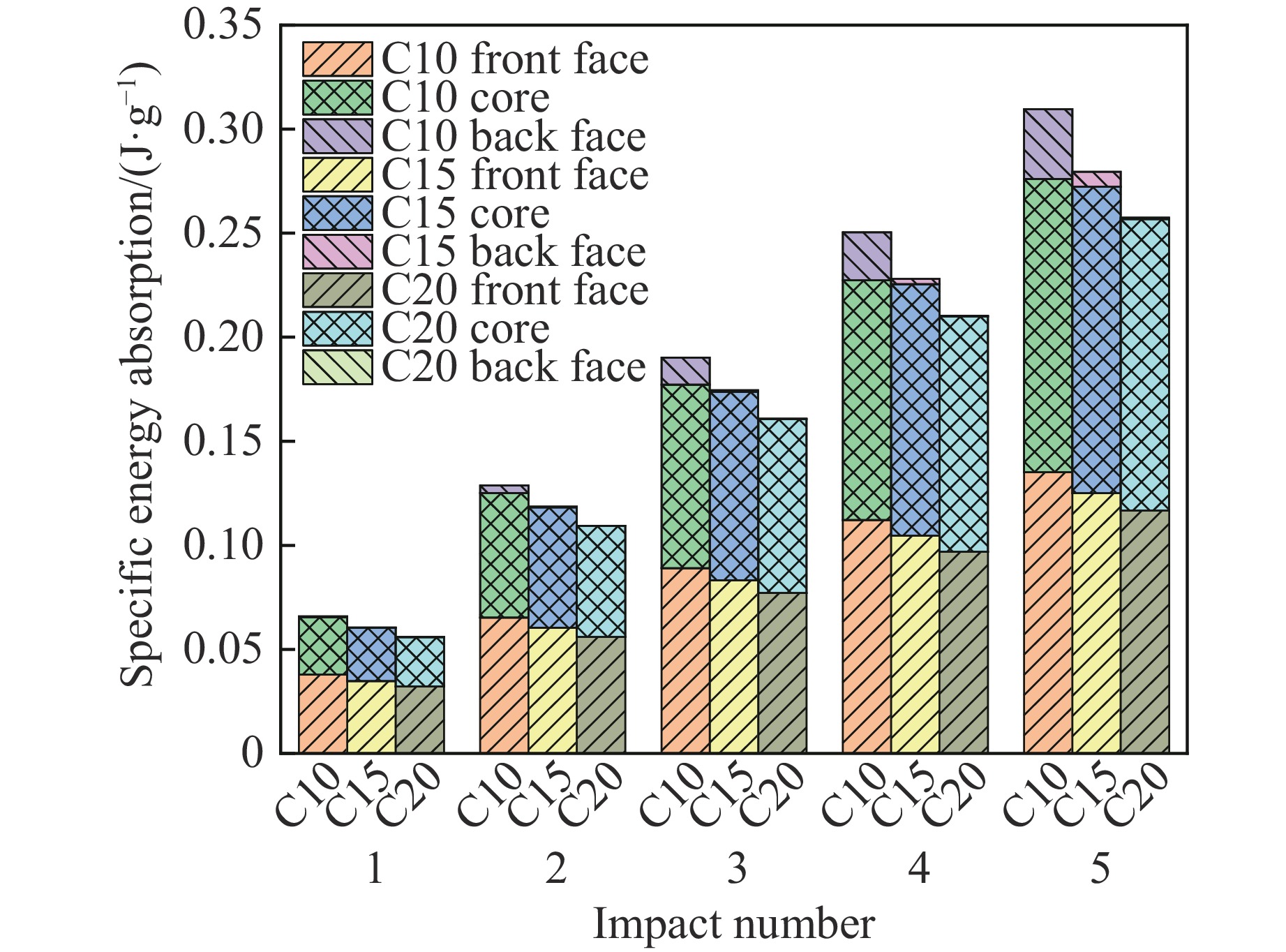
图15显示了3种芯层厚度夹芯壳结构的比吸能随冲击次数的变化规律。随着冲击次数的增加，泡沫铝夹芯壳结构的比吸能不断增加，C10的比吸能大于C15和C20。3种芯层厚度的夹芯壳结构的前、后面板以及芯层的能量吸收占比有明显的差异。芯层越厚，每次冲击的能量被前面板和芯层吸收得越多，后面板吸收的能量越少。C20的前面板和芯层的吸能占比高于C15和C10。随着冲击次数的增加，结构的前面板吸能占比逐渐降低，芯层和后面板吸能占比逐渐增大。

图  15  3种芯层厚度R50夹芯壳在18 J能量重复冲击下的比吸能

Figure  15.  Specific energy absorption of R50 sandwich shells with three core thickness under repeated impact of 18 J energy

下载: 全尺寸图片 幻灯片

3.4   冲击能量梯度的影响

为研究冲击能量梯度对泡沫铝夹芯壳重复冲击动态响应的影响，设刚性冲头质量为5.6 kg，冲击速度v分别为2.070、2.535和2.928 m/s，施加在泡沫铝夹芯壳结构上的冲击能量分别为12、18和24 J。在保持5次冲击总能量不变的条件下，设置了递增、均匀、递减3种不同梯度的冲击能量，记为E1、E2、E3，如表6所示。对3种冲击能量梯度下芯层厚度h_c=10 mm的R50泡沫铝夹芯壳的变形和能量耗散机理进行分析。

表  6  5次冲击的能量配置工况

Table  6.  Energy arrangement of five impacts

Case	Impact energy/J
	1st	2nd	3rd	4th	5th
E1	12	15	18	21	24
E2	18	18	18	18	18
E3	24	21	18	15	12

下载: 导出CSV 

| 显示表格

图16给出了R50泡沫铝夹芯壳在5次不同冲击能量冲击下的前、后面板挠度变化情况。可以看出，随着冲击次数的增加，夹芯壳结构的前、后面板挠度逐渐增大。3种能量梯度重复冲击载荷作用下泡沫铝夹芯壳结构的前、后面板挠度增加速率不同，冲击能量递增工况下的泡沫铝夹芯壳的前、后面板挠度增加速率最大，冲击能量递减工况下泡沫铝夹芯壳的前、后面板挠度增加的趋势逐渐变缓。第1次冲击后能量大部分被前面板和芯层吸收，后面板吸能很少，挠度增长不明显，差异较小。由于总冲击能量一定，5次冲击之后，3种冲击能量梯度下的前、后面板挠度逐渐趋于一致，E1工况下前、后面板的挠度较大，E3工况下前、后面板的挠度较小。

图  16  R50夹芯壳在3种能量梯度重复冲击下的中点挠度

Figure  16.  Midpoint deflection of R50 sandwich shell under repeated impact of three energy gradients

下载: 全尺寸图片 幻灯片

图17给出了R50泡沫铝夹芯壳在3种冲击能量梯度下的能量吸收情况。可以看出，由于3种能量梯度冲击下泡沫铝夹芯壳结构变形逐渐累积，芯层逐渐密实化，泡沫铝夹芯壳结构的变形速率不同，导致能量吸收性能出现差异。前2次冲击时，工况E3的冲击能量最大，工况E2次之，工况E1最小，较大的冲击使结构吸收了更多的能量。在第3次冲击时，3种工况的冲击能量相同，每次冲击能量的累积使结构在工况E3下表现出较强的能量吸收性能。当结构受到第4次冲击时，E1、E2、E3下的总冲击能量分别为66、72和78 J。因此，R50泡沫铝夹芯壳在前4次冲击时，工况E3的能量吸收较高。第5次冲击后，结构在3种工况下受到的总冲击能量均为90 J。R50泡沫铝夹芯壳在第5次冲击后，3种工况下的总能量吸收相近。工况E1下的R50泡沫铝夹芯壳的能量吸收略大于工况E2和工况E3，表明总能量一定时，冲击能量随冲击次数递增，可以提高结构的能量吸收性能。

图  17  R50夹芯壳在3种能量梯度重复冲击下的比吸能

Figure  17.  Specific energy absorption of R50 sandwich shell under repeated impact of three energy gradients

下载: 全尺寸图片 幻灯片

4.   结　论

通过数值模拟研究了重复冲击载荷下泡沫铝夹芯壳的变形和能量耗散机理。采用ABAQUS有限元软件建立了泡沫铝夹芯壳结构的有限元模型，将模拟结果与已有的实验结果进行对比，验证了所建模型的合理性。在此基础上，研究了重复冲击载荷作用下泡沫铝夹芯壳结构的变形规律和动态响应过程，分析结构的曲率半径、面板厚度分配、芯层厚度和冲击能量梯度等参数对结构力学性能的影响，得到的主要结论如下。

(1) 重复冲击载荷作用下，泡沫铝夹芯壳结构的变形不断累积增大，前面板发生局部弯曲变形，后面板发生整体弯曲变形，芯层逐渐变形直到密实化；随着冲击次数的增多，结构的能量吸收能力逐渐降低，整体抗弯刚度增大，冲击力峰值逐渐增大，冲击持续时间不断减小。

(2) 泡沫铝夹芯壳结构的几何参数，包括结构的曲率半径、面板厚度和芯层厚度对结构的变形和比吸能均有显著影响。结构的曲率半径越大，前、后面板在5次重复冲击之后的中点挠度越小，结构的比吸能越小；前面板越厚，前、后面板的中点挠度越小，结构的比吸能越小；前面板越薄，芯层的吸能越多；芯层越厚，结构后面板的中点挠度越小，结构的比吸能越小。

(3) 保持5次总冲击能量不变，在3种梯度冲击能量的作用下，递增能量作用下的泡沫铝夹芯壳结构的吸能最多，前、后面板的中点挠度最大，递减能量作用下泡沫铝夹芯壳结构的吸能最少，前、后面板的中点挠度最小。在给定的冲击能量下，前、后面板的厚度为1.5 mm，芯层厚度为15 mm的R50夹芯壳具有较优异的抗冲击性能。