A-Site Ordered Quadruple Perovskite Oxides: Structures, Properties and Prospects
-
摘要: A位有序四重钙钛矿氧化物
AA′3B4O12 具有丰富的物理性质和优异的材料性能,是当今凝聚态物理和材料科学的重要研究对象。相较于简单的ABO3型钙钛矿,在A位有序四重钙钛矿氧化物中,3/4的A位离子被过渡金属离子A′所取代,形成了1∶3的A/A′有序结构。因此,A位有序四重钙钛矿氧化物中的磁-电相互作用不再局限于B位子晶格内部,新颖的A′-A′、A′-B等磁-电相互作用也随之产生,从而展现出许多新现象和新物理机制,并为未来的实际应用提供了材料基础。围绕几种具有代表性的A位有序四重钙钛矿氧化物,回顾其研究脉络,对其晶体结构、物理性质和内在机理进行简单介绍,并对这类材料体系的研究方向和应用前景做出一些展望。Abstract: A-site ordered quadruple perovskite oxides with a formula asAA′3B4O12 exhibit multiple physical properties and superior performances, thus act as important subjects of current condensed matter physics and material science. Compared to the simple ABO3 perovskite, in the A-site ordered quadruple perovskite three quarters of the A atoms are replaced by transition metal Aʹ, forming ordered A/Aʹ occupancy with a 1∶3 ratio. As a result, the electric and magnetic interactions such as Aʹ-Aʹ and Aʹ-B can occur, leading to novel phenomena and new physics. Here we focus on several representative A-site ordered quadruple perovskites, recall their researches, briefly introduce their structures, physical properties and inner mechanisms, and discuss the opportunities for both fundamental studies and potential applications.-
Key words:
- high-pressure synthesis /
- perovskite oxide /
- dielectricity /
- charge order /
- multiferroics /
- half metal
-
ABO3钙钛矿氧化物是以CaTiO3为代表的具有类似的或衍生结构的材料体系。钙钛矿氧化物的研究具有悠久的历史,其灵活多变的结构使其可以容纳多种多样的离子组合,从而产生了丰富多彩的物理性质[1–3]。如果在钙钛矿的A位引入过渡金属离子,特别是将3/4的A离子替换为过渡金属离子Aʹ并形成1∶3的A/A′位有序结构,则可获得化学式为
AA′3B4O12 的A位有序四重钙钛矿(A-site ordered quadruple perovskite)氧化物。由于A′位、B位多个位点容纳磁性离子,其丰富的磁-电相互作用可以使A位有序四重钙钛矿氧化物进一步演生出一系列新颖的物理性质[4]。尽管A位有序四重钙钛矿的首次发现可以追溯至20世纪60年代[5],然而,直至21世纪初,其新颖的物理性质和优异的材料性能才引起了广泛的关注。近20余年来,在A位有序四重钙钛矿氧化物中已发现诸多引人入胜的物理现象,如高介电常数[6]、电荷有序[7]、铁电性[8]、多铁性[9]、高温磁性[10]、巨磁电阻[11]、半金属性[12]、催化活性[13]等。如今,A位有序四重钙钛矿氧化物的研究方兴未艾,许多新材料有待制备,许多新现象和新物性有待发现,相关的物理机制需要进一步解释和完善。本文着眼于本课题组所关注的几类具有代表性的A位有序四重钙钛矿氧化物,回顾其研究脉络,介绍其物理性质和研究进展,以期抛砖引玉,为这一领域的研究添砖加瓦。1. A位有序四重钙钛矿氧化物的结构
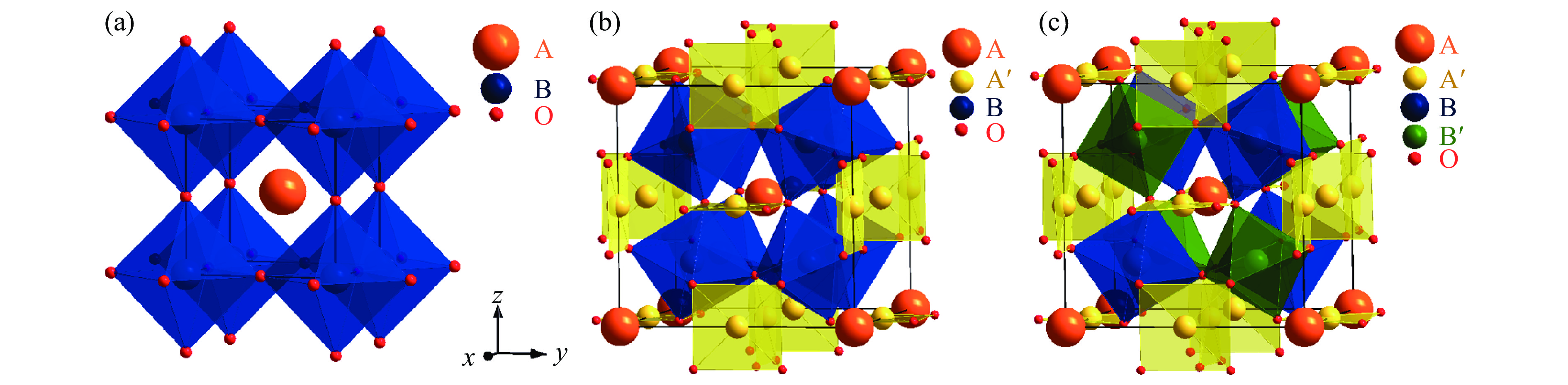
理想的ABO3型钙钛矿的结构如图1(a)所示:A位通常为碱金属、碱土金属或稀土金属,与其周围12个O形成AO12正二十面体结构;B位通常为过渡金属,与其周围的6个O形成BO6正八面体结构。对于ABO3型钙钛矿,其A位通常是非磁性离子,作为结构框架和电子库而存在,过渡金属离子通常位于B位,因而其磁-电相互作用通过B-B路径发生。如果能在A位也引入过渡金属离子,那么就可以引入更丰富的磁-电相互作用路径,如A-B等,从而产生新颖的物理性质。事实证明,将3/4的A位非磁性离子替换为过渡金属离子Aʹ,可以形成一种全新的A位有序四重钙钛矿
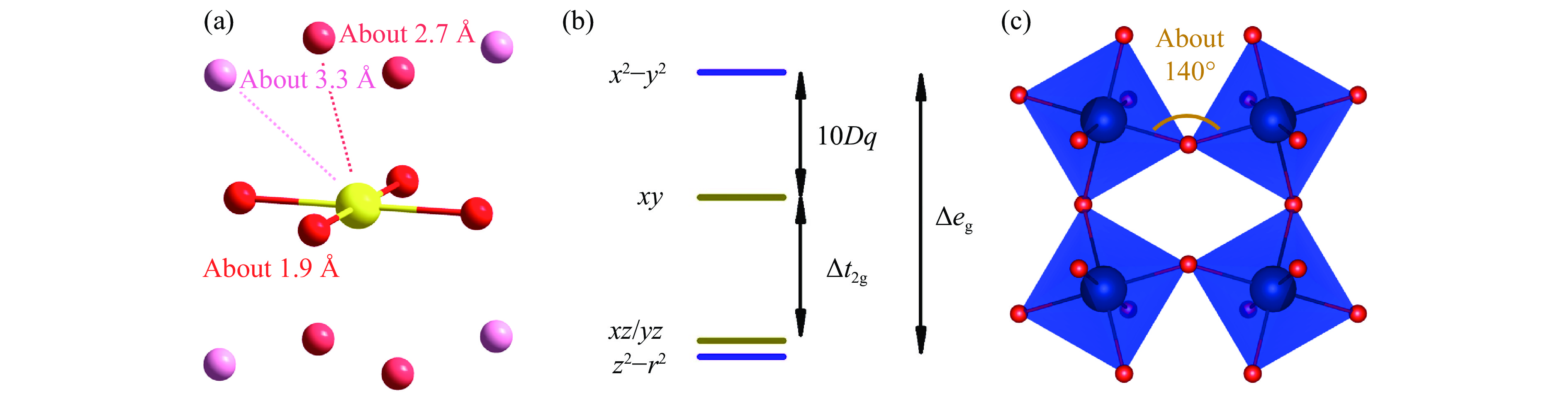
AA′3B4O12 ,如图1(b)所示。此外,B位也可形成有序结构,如岩盐(rock-salt)序,其化学式可写为AA′3B2B′2O12 ,如图1(c)所示。在A位有序四重钙钛矿氧化物中,磁性离子的引入不仅改变了A位的组分,更显著的变化在于A′位磁性离子不再与12个O形成正二十面体结构,而是形成3组键长不同的A′―O键。如图2(a)所示,A′与4个最近邻O形成了A′O4平面四边形结构,除此之外,还有4个次近邻和4个次次近邻O。由于次近邻和次次近邻的O距离A′较远,因此,一般仅考虑A′O4平面四边形结构。如图2(b)所示,在平面四边形晶体场中,由于z方向不存在O离子(也可以看作z方向的配位O离子处于无限远处),从而使与z相关的轨道(z2–r2、xz和yz)相对x2–y2和xy轨道的能量大幅降低。因此,具有强的杨-泰勒(Jahn-Teller)效应的离子如Cu2+(3d9,eg轨道仅有1个空穴)和Mn3+(3d4,eg轨道仅有1个电子)很容易占据A′位。目前,占据Aʹ位的过渡金属离子通常为上述Cu2+和Mn3+,也有一些其他离子,如Co2+、Fe2+等[14–15]。由于A位与A′位O配位环境的巨大不同,A位和A′位离子将自发形成1∶3的有序结构,致使其晶格常数也扩大至ABO3型钙钛矿的2倍,原胞所含原子数扩大至4倍(图1),此即A位有序四重钙钛矿名称的来源。另一方面,由于A′位占据过渡金属离子,相比于ABO3型钙钛矿,其A位离子的平均半径明显减小,从而造成A位和B位离子尺寸的失配。为了补偿这一晶格失配,BO6八面体将会出现较为剧烈的倾斜,相比于理想的180°键角,A位有序四重钙钛矿氧化物中的B―O―B键角约为140°,如图2(c)所示。A位有序四重钙钛矿氧化物中这种剧烈的晶格畸变难以在常压下形成,往往需要外部压力的推动。目前,高压手段是合成A位有序四重钙钛矿氧化物最常用的方法之一。A位有序四重钙钛矿氧化物中磁性A′位离子的引入使其磁-电相互作用不再局限于B位,Aʹ-Aʹ、Aʹ-B等新的相互作用随之发生,并由此产生了丰富的物理性质。
 图 2 (a) Aʹ的氧配位示意图(黄色表示Aʹ离子,红色表示O离子,颜色由深至浅表示Aʹ―O键长由短至长),(b) AʹO4平面四边形晶体场示意图(10Dq为d轨道(t2g、eg)的劈裂,Δt2g、Δeg分别为t2g(xy、xz、yz)和eg(x2–y2、z2–r2)轨道的劈裂),(c) BO6八面体的倾斜(蓝色表示B离子,红色表示O离子)Figure 2. (a) Coordination of the Aʹ site, the Aʹ ion is displayed in yellow, the O anions are displayed in red, and the different colors of O indicate the different Aʹ―O bond lengths; (b) crystal field of AʹO4 square planar, the 10Dq represents the split of the d orbit (t2g, eg), the Δt2g and Δeg represent the split of the t2g (xy, xz, yz) and eg (x2–y2, z2–r2) orbits, respectively; (c) tilt of the BO6 octahedra, the B ions are displayed in blue, and the O anions are displayed in red
图 2 (a) Aʹ的氧配位示意图(黄色表示Aʹ离子,红色表示O离子,颜色由深至浅表示Aʹ―O键长由短至长),(b) AʹO4平面四边形晶体场示意图(10Dq为d轨道(t2g、eg)的劈裂,Δt2g、Δeg分别为t2g(xy、xz、yz)和eg(x2–y2、z2–r2)轨道的劈裂),(c) BO6八面体的倾斜(蓝色表示B离子,红色表示O离子)Figure 2. (a) Coordination of the Aʹ site, the Aʹ ion is displayed in yellow, the O anions are displayed in red, and the different colors of O indicate the different Aʹ―O bond lengths; (b) crystal field of AʹO4 square planar, the 10Dq represents the split of the d orbit (t2g, eg), the Δt2g and Δeg represent the split of the t2g (xy, xz, yz) and eg (x2–y2, z2–r2) orbits, respectively; (c) tilt of the BO6 octahedra, the B ions are displayed in blue, and the O anions are displayed in red2. A位有序四重钙钛矿氧化物的物理性质
2.1 反常高介电常数:ACu3Ti4O12
CaCu3Ti4O12是首个被报道的A位有序四重钙钛矿氧化物,由Deschanvres等[5]于1967年首先制备,将钙钛矿CaTiO3中3/4的A位Ca2+替换为Cu2+。由于Cu2+是杨-泰勒离子,因此可以稳定存在于CuO4平面四边形的配位中,从而形成A位有序四重钙钛矿氧化物结构。这一特殊结构最终由Bochu等[16]于1979年通过X射线衍射(X-ray diffraction,XRD)实验确认。CaCu3Ti4O12的发现引起了人们对这一新材料体系的研究兴趣,并随之制备出一系列A位有序四重钙钛矿氧化物材料[17–26]。但是,自CaCu3Ti4O12被发现后的20年里,人们的研究主要集中于新材料的制备和结构。直到2000年,Subramanian等[6]和Ramirez等[27]在CaCu3Ti4O12中首次发现了反常高的相对介电常数,随后,在一系列具有不同A位离子的ACu3Ti4O12体系中均发现了反常高的介电常数[28],从而引发了对ACu3Ti4O12及A位有序四重钙钛矿氧化物的物性、机理和应用的研究热潮。
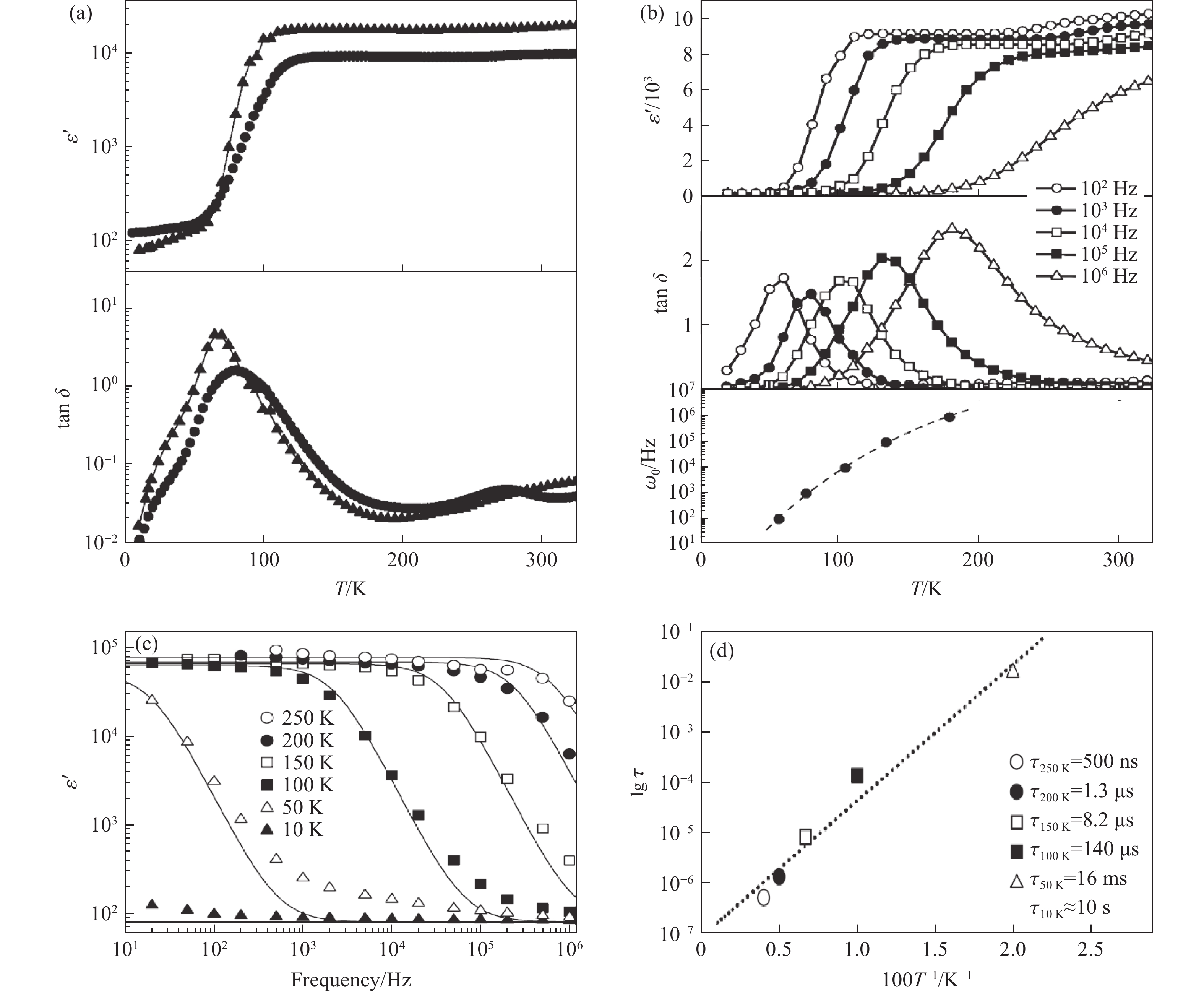
以CaCu3Ti4O12为例,其相对介电常数的实部(εʹ)和损耗因子(tan δ)随温度(T)的变化关系如图3(a)所示:其εʹ在100~400 K的温度范围内高达105量级(一般材料的εʹ不高于102量级),并且基本不随温度变化;在100 K附近εʹ发生突变,降低3个数量级,tan δ也在此处出现极大值。另一方面,其介电响应的特征频率(ω0)随温度的升高而升高,如图3(b)~图3(d)所示。
CaCu3Ti4O12出现如此反常高的介电常数是出乎人们意料的。从对称性上看,相较于典型的铁电体BaTiO3,在具有A位有序四重钙钛矿氧化物结构的CaCu3Ti4O12中,由于TiO6八面体的倾斜,其四重对称性被破坏,Ti4+只能沿着3次轴发生位移,而同一原胞的4个TiO6八面体中,Ti4+的位移恰好相互抵消,因此无法产生宏观铁电极化和铁电相变[6]。第一性原理计算也表明,CaCu3Ti4O12的εʹ为45~50[30],远低于实验观测值。另一方面,CaCu3Ti4O12的εʹ在100 K处发生突变,减小了3个数量级,并且随着频率的增加,突变温度也升高至200 K。而XRD和中子粉末衍射(neutron powder diffraction,NPD)均表明,CaCu3Ti4O12在35 K至室温范围内保持
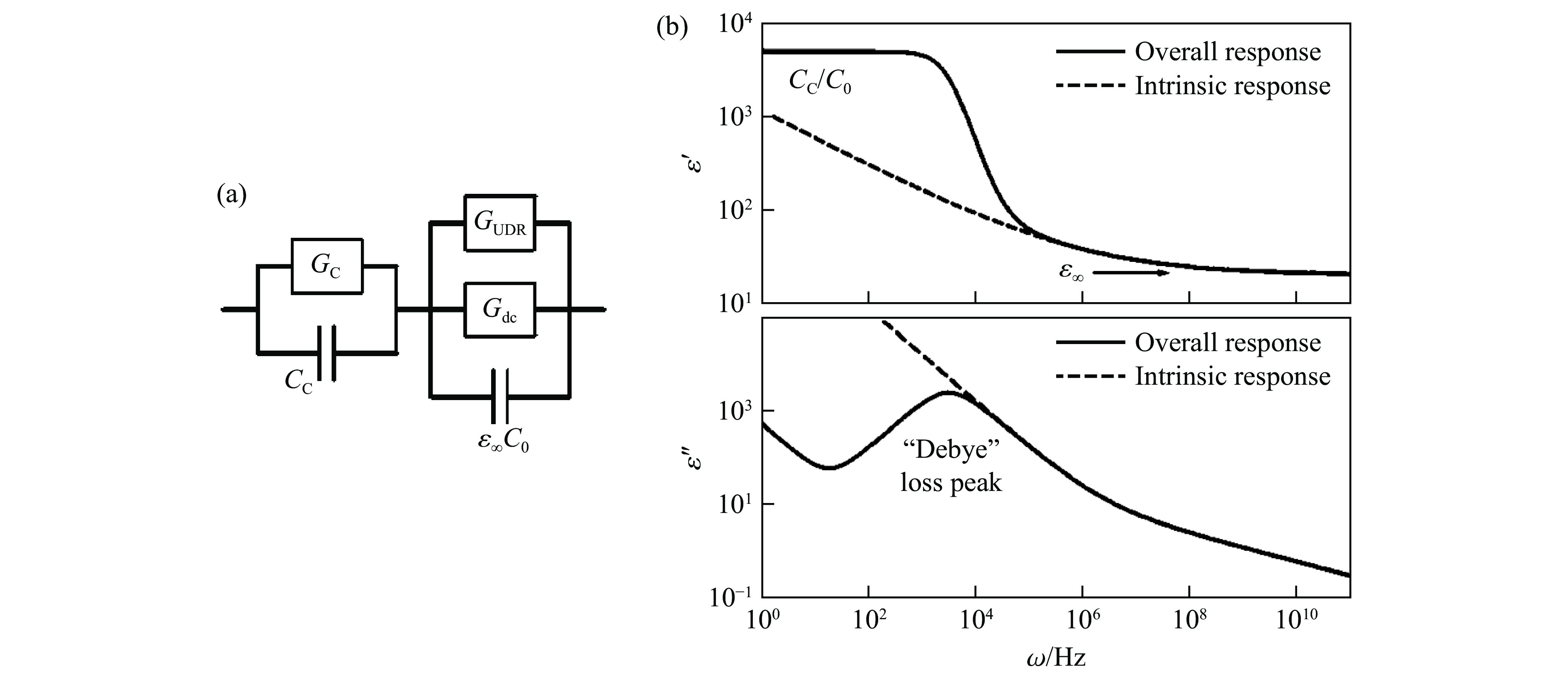
Im¯3 的立方结构[6, 27],仅在其奈尔(Néel)温度TN=25 K附近发生了Cu2+磁有序导致的反铁磁转变[31–32]。上述行为均预示着CaCu3Ti4O12的反常高的介电常数很可能具有非本征的起源,如晶界间的空间电荷、电极与样品间的接触电阻等。2002年,Lunkenheimer等[33]指出,CaCu3Ti4O12的反常高介电常数很可能来自材料自身和非本征因素(晶格缺陷、晶界、接触电阻等)共同参与的Maxwell-Wagner机制[34–35],这一机制最早的实验证明可追溯至钇铁石榴石(Y3Fe5O12,YIG)多晶块材的高介电行为[36]。Maxwell-Wagner机制可用如图4(a)所示的等效电路表示:其中GUDR、Gdc、ε∞C0分别表示本征交流电导、本征直流电导以及本征高频电容(ε∞为高频相对介电常数,C0为真空电容),三者代表材料的本征贡献;此外,GC和CC分别表示非本征的电导和电容。图4(a)所示的等效电路的介电行为随频率的变化关系见图4(b)。可以看到,εʹ在低频区基本不随频率变化,呈现出一个平台,随着频率的升高,εʹ发生突变,出现几个数量级的衰减,同时,相对介电常数的虚部(εʹʹ)也出现一个极大值,与CaCu3Ti4O12的实验测量结果(图3(c))一致。这一观点被随后的大量实验证明。首先,在极高质量、无缺陷的CaCu3Ti4O12薄膜中,测得了本征的εʹ随频率的变化行为(指数型响应,如图4(b)虚线所示),本征的εʹ在102量级[37]。另一方面,一系列ACu3Ti4O12的阻抗谱测量结果与Maxwell-Wagner机制相吻合,ACu3Ti4O12的本征εʹ在102量级且本征电导预示着ACu3Ti4O12是半导体[38–41]。至此,晶格与晶界共同参与的Maxwell-Wagner机制导致ACu3Ti4O12产生非本征、反常高的介电常数这一解释逐渐被研究者广泛接受。
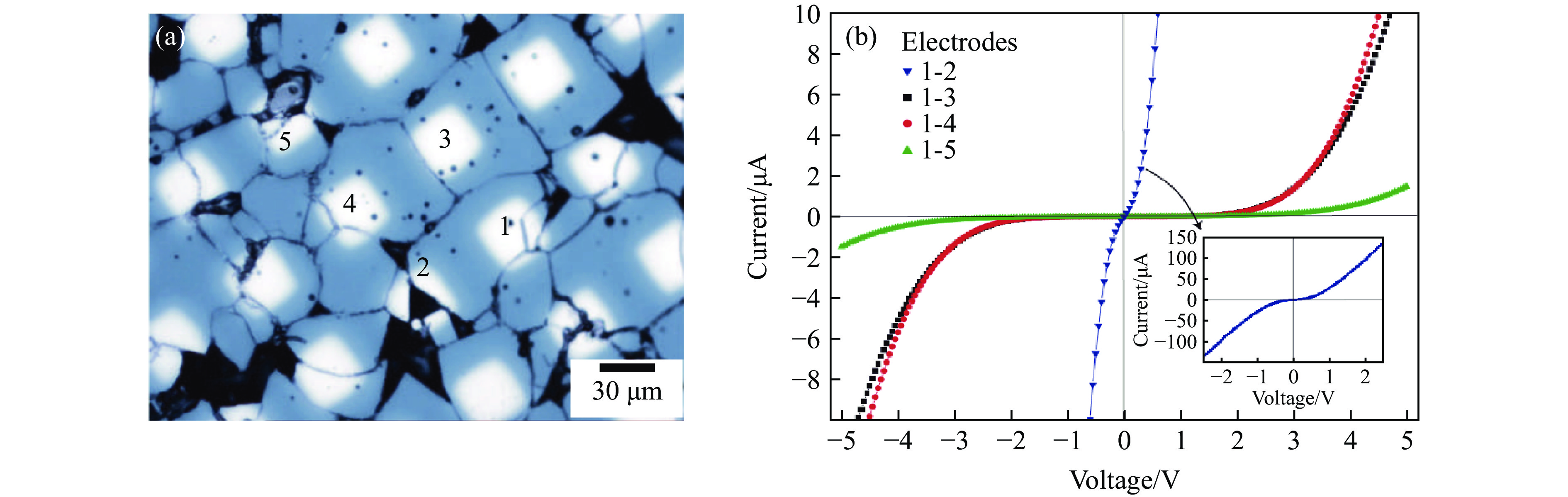
Chung等[42]通过微触点(microcontact)的电流-电压(I-V)曲线直观地展示了晶界对CaCu3Ti4O12电学性质的影响。如图5所示,在CaCu3Ti4O12晶粒内部(曲线1-2),I-V曲线表现出欧姆行为,其电阻率为310 Ω·cm,表明CaCu3Ti4O12为半导体,与理论计算以及阻抗测量结果一致[38–41]。另一方面,不同晶粒间(曲线1-3、曲线1-4和曲线1-5)的I-V曲线呈现显著的偏压,且偏压大小与接触点间的晶界数量呈正相关,表明晶界处存在显著的静电能垒。进一步计算得到的非线性系数ξ高达900(I∝V ξ),显著高于商用的ZnO基陶瓷材料[43]。值得注意的是,CaCu3Ti4O12的晶界性质还可以通过烧结过程、掺杂以及气体吸附进行有效调控[40, 44–49]。因此,尽管具有非本征的起源,以CaCu3Ti4O12为代表的一系列A位有序四重钙钛矿氧化物所具有的高介电常数以及大的非线性I-V系数使其在介电材料、电涌保护器、气敏/压敏器件等领域具有巨大的应用潜力。
2.2 电荷有序:ACu3Fe4O12
2008年,Yamada等[50]通过15 GPa的高压手段合成了一种新型A位有序四重钙钛矿CaCu3Fe4O12,该材料不仅具有罕见的Fe4+高价态,而且在其居里(Curie)温度TC=210 K处由于Cu和Fe自旋的反平行排列发生亚铁磁相变[51–52],并发生电荷歧化(charge disproportionation)2Fe4+ → Fe3++Fe5+,其B位Fe3+和Fe5+具有岩盐型有序结构,空间群由高温的
Im¯3 (图1(b))变为低温的Pn¯3 (图1(c))。2009年,Long等[7, 53]在LaCu3Fe4O12中观察到TN=393 K处Aʹ位Cu与B位Fe之间的电荷转移行为3Cu2++4Fe3.75+→3Cu3++4Fe3+,并伴随结构相变、反铁磁转变(B位Fe3+反铁磁序)、金属-绝缘体转变以及负热膨胀,如图6所示。随后,Yamada等[54]继续替换不同的A位离子,并在SrCu3Fe4O12中发现较高的负热膨胀性,不同于CaCu3Fe4O12(不发生负热膨胀)和LaCu3Fe4O12(相变窄温区的负热膨胀),SrCu3Fe4O12在170~270 K的宽温区内具有近线性的负热膨胀系数−2.26×10−5 K−1,与当时所知的最大负热膨胀系数纪录(−2.5×10−5 K−1)[55]相当。尽管这一材料体系均存在电荷有序,但具体发生B位Fe自身的电荷歧化,还是Aʹ位Cu与B位Fe之间的电荷转移,仍与具体的A位离子密切相关。另外,负热膨胀这一特性似乎仅出现在具有电荷转移的材料如LaCu3Fe4O12和SrCu3Fe4O12,而电荷歧化的CaCu3Fe4O12并未出现负热膨胀行为。 图 6 LaCu3Fe4O12在TN=393 K的多种转变:(a) Cu―O键、Fe―O键的键长随温度的变化关系;(b) 体积随温度的变化关系;(c) 穆斯堡尔(Mössbauer)谱的光吸收随运动速度的变化关系;(d) 磁化率(χ)和电阻率(ρ)随温度的变化曲线(插图为磁矩M随温度的变化曲线)[7]Figure 6. Multiple transitions of LaCu3Fe4O12 at TN=393 K: (a) temperature-dependent Cu―O and Fe―O bond lengths; (b) temperature-dependent negative thermal expansion; (c) Mössbauer spectra, the velocity-dependent absorption; (d) temperature-dependent magnetic susceptibility (χ) and resistivity (ρ), the inset displays the temperature-dependent magnetization (M)[7]
图 6 LaCu3Fe4O12在TN=393 K的多种转变:(a) Cu―O键、Fe―O键的键长随温度的变化关系;(b) 体积随温度的变化关系;(c) 穆斯堡尔(Mössbauer)谱的光吸收随运动速度的变化关系;(d) 磁化率(χ)和电阻率(ρ)随温度的变化曲线(插图为磁矩M随温度的变化曲线)[7]Figure 6. Multiple transitions of LaCu3Fe4O12 at TN=393 K: (a) temperature-dependent Cu―O and Fe―O bond lengths; (b) temperature-dependent negative thermal expansion; (c) Mössbauer spectra, the velocity-dependent absorption; (d) temperature-dependent magnetic susceptibility (χ) and resistivity (ρ), the inset displays the temperature-dependent magnetization (M)[7]通过第一性原理计算,Hao等[56]研究了CaCu3Fe4O12的电子结构,发现Fe-3d态密度在费米(Fermi)面(EF)附近具有与O-2p态密度相似的特征,预示着Fe―O之间存在强的共价键。另外,Li等[57]研究了LaCu3Fe4O12的电子结构,并指出其Cu-Fe电荷转移是通过Cu-3dxy→O-2px, 2py→O-2pz→Fe-3dxz, 3dyz这一路径发生。他们还指出:LaCu3Fe4O12的体积由Fe―O键长支配,电荷转移使Fe总体上得到电子(Fe3.75+→Fe3+),因而键长增加导致负热膨胀;而电荷歧化发生于Fe自身,Fe―O的平均键长没有明显变化,因此不发生体积突变。这一结论也与实验[54]相一致。Chen等[58]也通过研究Ca1−xLaxCu3Fe4O12固溶体的负热膨胀性质指出,CaCu3Fe4O12的Fe自身的电荷歧化可看作其配体空穴(ligand hole)局域于B位Fe附近而导致,而LaCu3Fe4O12的Cu-Fe电荷转移可以看作其配体空穴局域于Aʹ位Cu附近所致。此外,Allub等[59]还利用热力学模型研究了ACu3Fe4O12的相变,指出ACu3Fe4O12的电荷有序与Fe的最近邻跃迁项t(nearest-neighbor hopping term)相关:当t较小时(Fe-Fe间铁磁相互作用较弱),基态为反铁磁绝缘体,并发生Cu-Fe间电荷转移;当t较大时(Fe-Fe间铁磁相互作用较强),基态为铁磁金属,相变时Aʹ位Cu的电子数不变,发生Fe自身的电荷歧化。
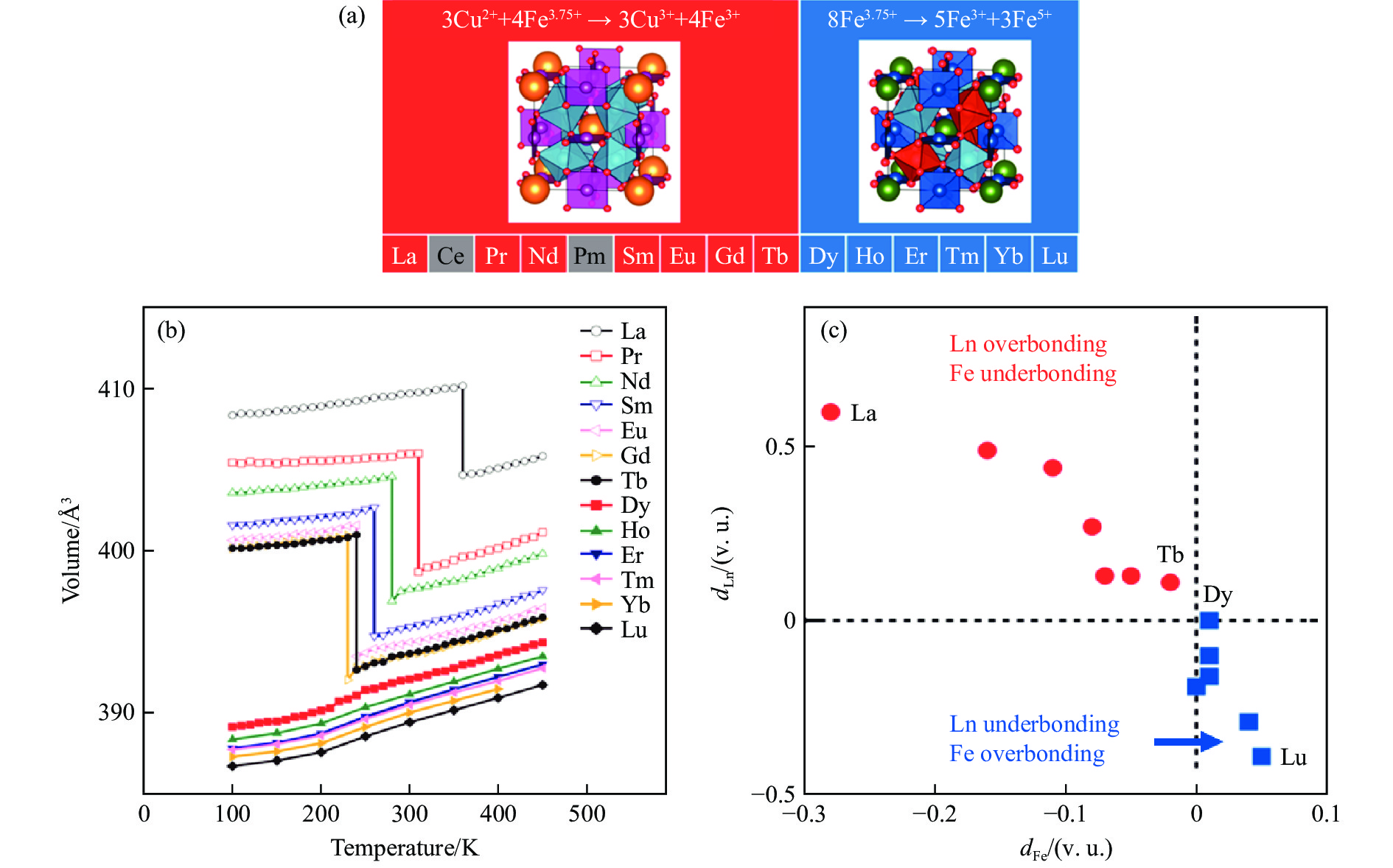
2012年,Etani等[60]指出,ACu3Fe4O12的电荷有序形式可简单地由A位离子半径决定:当A位离子半径较大时(A=La3+,Sr2+),发生电荷转移;当A位离子半径较小时(A=Ca2+,Y3+),发生电荷歧化。随后,Yamada等[61]系统地研究了A位为镧系元素时LnCu3Fe4O12的电荷有序行为,发现当Ln为离子半径较大的La~Tb时,发生电荷转移和负热膨胀;而当A位离子为半径较小的Dy~Lu时,发生电荷歧化,如图7(a)和图7(b)所示。通过进一步研究A位镧系离子和B位Fe离子的键长和化合价,如图7(c)所示,他们发现,对于半径较大的Ln(La~Tb),Ln处于过键合(overbonding)状态(价态高于自由离子,Ln―O键被压缩),而Fe处于欠键合(underbonding)状态(价态低于自由离子,Fe―O键被拉伸);反之,对于半径较小的Ln(Dy~Lu),Ln处于欠键合状态,而Fe处于过键合状态。
 图 7 (a) LnCu3Fe4O12的电荷有序形式总览;(b) LnCu3Fe4O12在相变温度附近的体积随温度的变化曲线;(c) Ln和Fe的键合状态(d为价键求和(bond valence sum,BVS)计算得到的价态与自由离子价态之差,d < 0表示欠键合,d > 0表示过键合)[61]Figure 7. (a) An overview of charge order of LnCu3Fe4O12; (b) temperature-dependent volume of LnCu3Fe4O12; (c) correlation between dLn and dFe (d is the difference between bond valence sum (BVS) and ionic valence state. d < 0 indicates underbonding and d > 0 indicates overbonding.)[61]
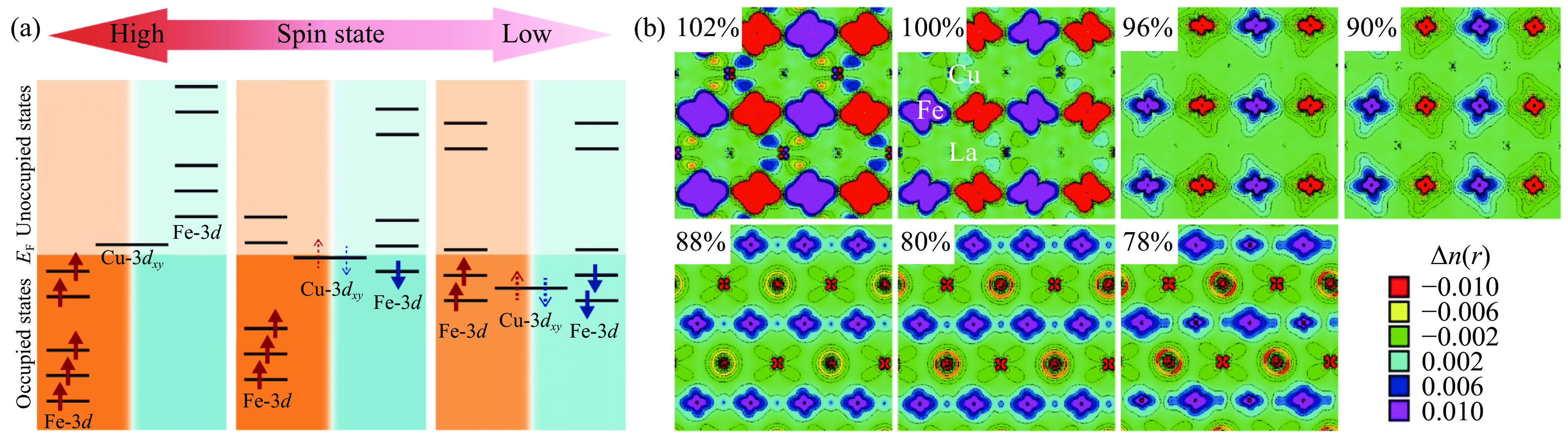
图 7 (a) LnCu3Fe4O12的电荷有序形式总览;(b) LnCu3Fe4O12在相变温度附近的体积随温度的变化曲线;(c) Ln和Fe的键合状态(d为价键求和(bond valence sum,BVS)计算得到的价态与自由离子价态之差,d < 0表示欠键合,d > 0表示过键合)[61]Figure 7. (a) An overview of charge order of LnCu3Fe4O12; (b) temperature-dependent volume of LnCu3Fe4O12; (c) correlation between dLn and dFe (d is the difference between bond valence sum (BVS) and ionic valence state. d < 0 indicates underbonding and d > 0 indicates overbonding.)[61]容易想到,Fe―O的键合强度显著影响Fe的电子结构。Rezaei等[62]通过理论计算指出,当Fe―O欠键合时,Fe的价态较低,其周围电子较多,因此具有较大的自旋量子数。此时,强的磁交换能将使Fe的上自旋轨道降低,其结果是Fe的下自旋轨道和Cu的3dxy轨道处于费米面以上,如图8(a)左侧所示。因此,电子将倾向占据Fe的轨道,发生Cu-Fe间的电荷转移。反之,当Fe―O过键合时,Fe的价态较高,具有较小的自旋量子数,此时的能级示意图如图8(a)右侧所示。因此,Fe的下自旋能带和Cu的3dxy轨道能量均与Fe的上自旋能带接近,因此,电子倾向于同时占据3种能带,发生Fe自身的电荷歧化,并且形成反铁磁结构。另一方面,通过压力也可以调节键合强度,从而调控其电荷有序。Meng等[63]计算了LaCu3Fe4O12在不同体积下的电子结构,如图8(b)所示,在100%体积下的计算表明,其为Cu-Fe电荷转移型电荷有序,与实验结果(图6)[7] 一致,随着压力升高(体积减小),电荷转移逐渐受到抑制,并转变为Fe离子间的电荷歧化。类似地,通过化学压力同样也可以实现对ACu3Fe4O12磁性、电荷有序、负热膨胀等性质的调控[58, 64]。
除ACu3Fe4O12体系以外,还有一些材料通过电荷有序形成A位有序四重钙钛矿结构。如ABO3型钙钛矿PbCoO3具有电荷有序的
Pb2+Pb4+3Co2+2Co3+2O12 型结构,不仅A位具有1∶3的有序结构,B位Co2+和Co3+也形成了岩盐型有序,具有立方的Pn¯3 空间群[65]。并且,这一精细的电荷有序态可以被压力调控,实现Pb4+-Co2+间的电荷转移,并诱导Co2+自旋态转变,同时伴随着结构相变和金属-绝缘体相变,如图9(a)所示[66]。令人惊讶的是,一些二元氧化物通过电荷有序也可以形成A位有序四重钙钛矿结构。例如:对Mn2O3进行高压处理,可以形成A位有序四重钙钛矿结构的ζ-Mn2O3相Mn2+Mn3+3Mn3.25+4O12 ,如图9(b)[67]所示。类似地,有迹象表明,Fe2O3在高压下也出现了具有A位有序四重钙钛矿结构的ζ-Fe2O3相,如图9(c)[68]所示。因此,A位有序四重钙钛矿氧化物不仅为研究多种丰富的电荷有序提供了重要的材料基础,其负热膨胀性质也为材料科学和实际运用提供了新的材料体系。此外,通过压力调控其电荷序以及结构、磁学、电学等性质,在地球物理等交叉学科研究中也具有重要意义。2.3 磁电多铁性:AMn3Cr4O12
2003年,2种重要的多铁性材料BiFeO3[69]和TbMnO3[70]掀起了多铁性研究的热潮。BiFeO3是目前仅有的在室温以上同时具有铁磁性和铁电性的多铁性材料,它在TC=1103 K和TN=643 K分别发生铁电相变和反铁磁相变,其电极化可达60 μC/cm2,并具有1.0玻尔磁子每分子式(μB/(f. u.))的饱和磁矩[71]。因此,BiFeO3所具有的大的电极化、强的磁性以及极高的特征温度使其具有相当理想的应用前景。然而,BiFeO3的电极化和磁性具有不同的起源,前者来自Bi3+的位移(与传统铁电材料BaTiO3类似),后者来自Dzyaloshinskii-Moriya(DM)相互作用引起的Fe3+螺旋磁结构。以BiFeO3为代表的多铁性材料被称为Ⅰ类多铁性材料[72–73],它们的铁电性和铁磁性具有不同的来源,因而两者的耦合较弱(磁电耦合系数α<3 ps/m)[74]。
另一种ABO3型钙钛矿TbMnO3在28 K处出现介电常数异常,同时产生电极化(0.08 μC/cm2)[70]。由于TbMnO3中并没有具有孤对电子的离子,因此,其电极化应该与BiFeO3有着不同的成因。进一步的研究表明,其电极化还受到磁场的调控,预示着较强的磁电耦合效应。因此,TbMnO3是具有磁电耦合效应的多铁性材料,也是第一个被发现的Ⅱ类多铁性材料。与Ⅰ类多铁性材料不同,Ⅱ类多铁性材料的铁电性通常由特殊的磁结构所引起,因而其铁电性具有磁性起源,并具有强的磁电耦合[72–73, 75]。
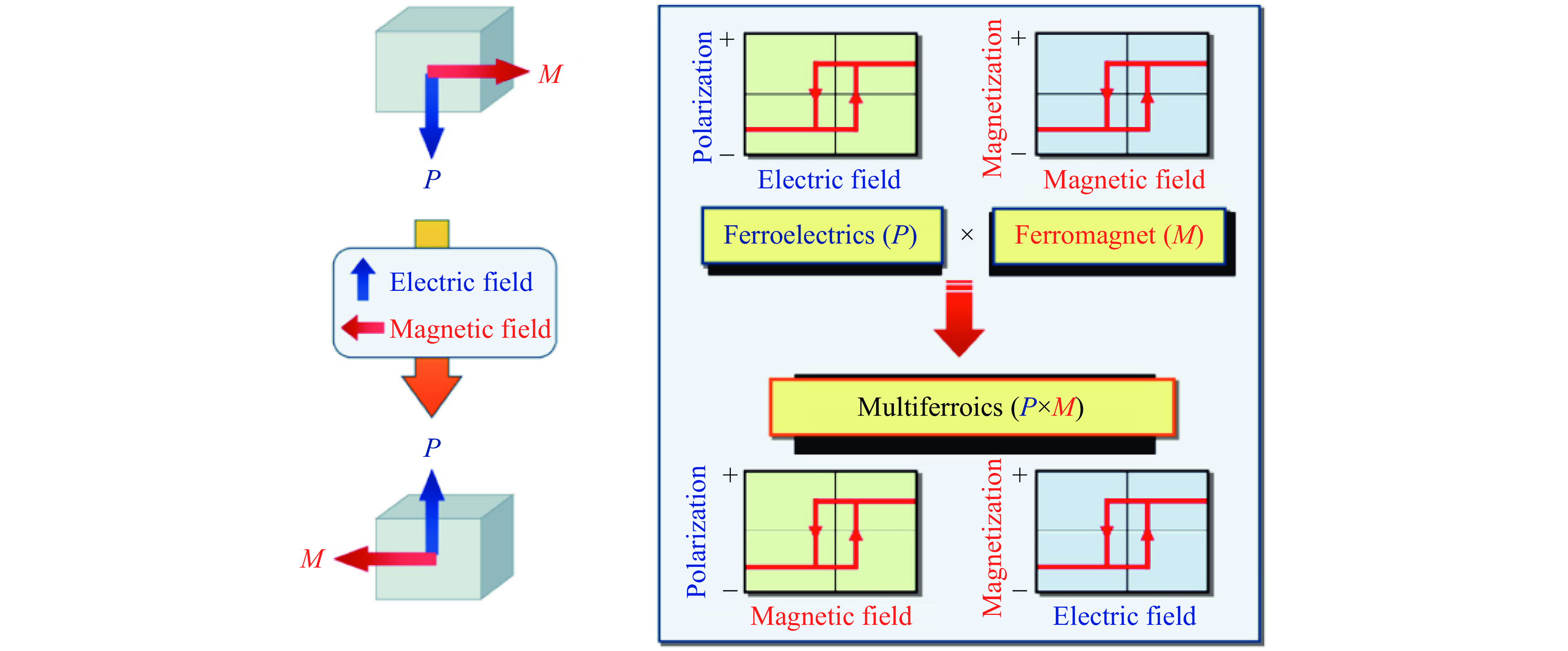
磁电多铁性材料以其潜在的应用而受到广泛的关注,如图10所示,磁电多铁性材料的磁、电性质可以相互响应和调控,即磁(电)场不仅可以改变磁(电)性,而且可以同时改变电(磁)性。因此,磁电多铁性材料在存储器件[76]、逻辑运算[77]、磁强计[78]以及磁电天线[79]等领域具有极为广阔的应用前景。
A位有序四重钙钛矿
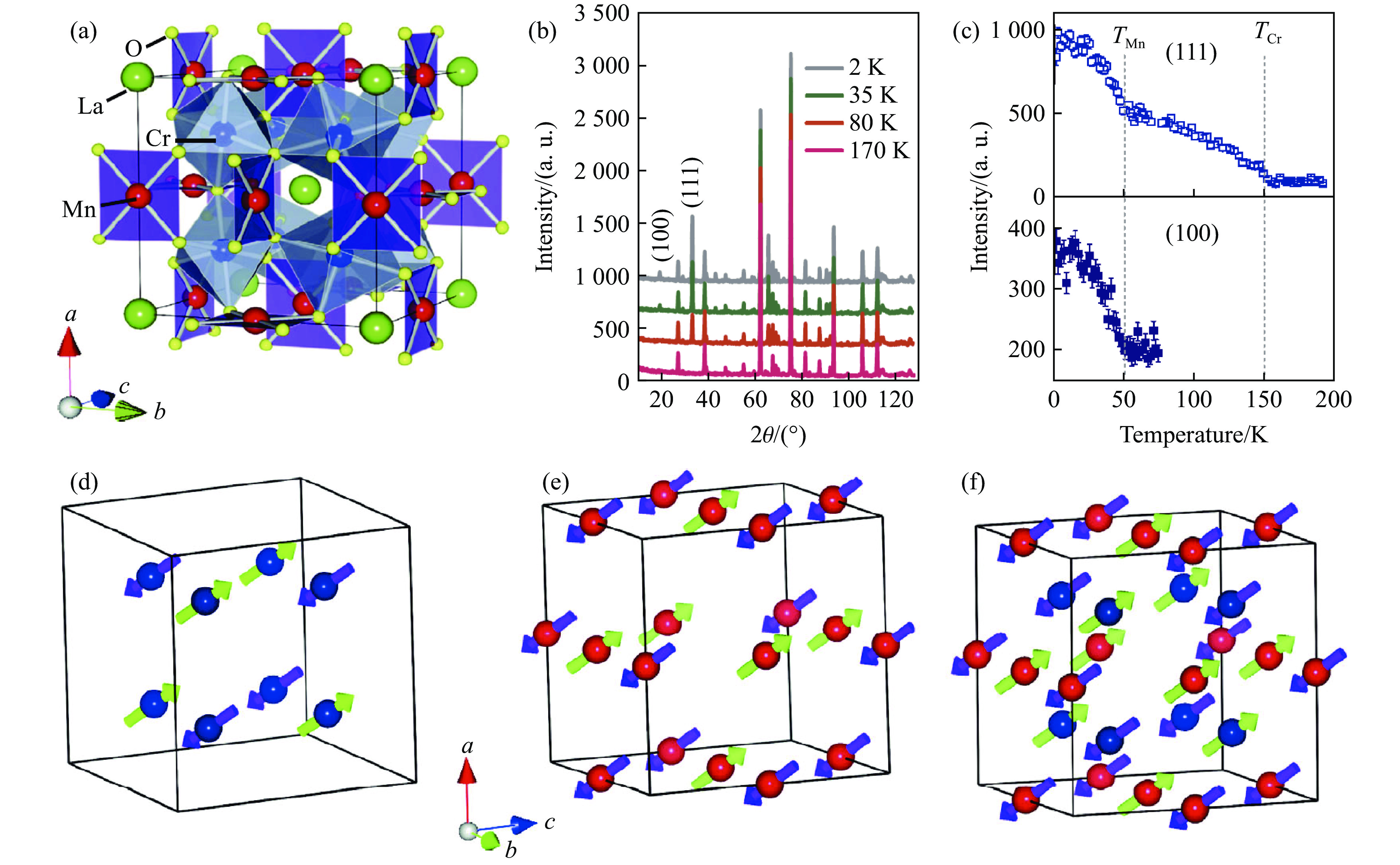
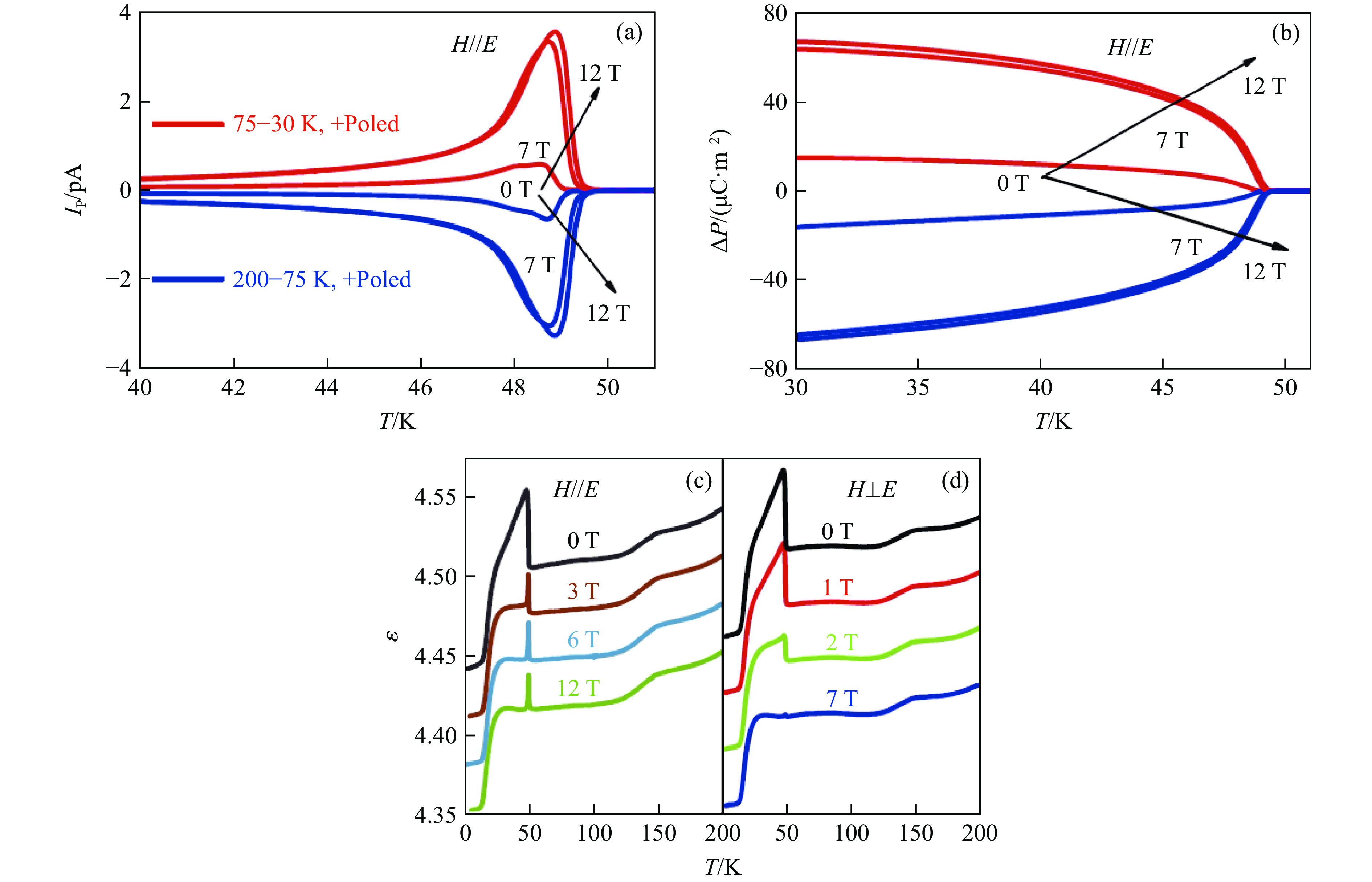
AA′3B4O12 是研究磁电耦合多铁性的理想材料体系。在这一材料体系中,由于A′位与B位均容纳过渡金属离子,从而使磁电耦合不再局限于B位,而是延伸到整个晶格结构之中。这一改变不仅使AA′3B4O12 具有丰富的磁电耦合相互作用,并且可以通过选择合适的A′位和B位离子,实现磁电耦合的有效调控。2009年,Long等[80]首次报道了一种新型A位有序四重钙钛矿LaMn3Cr4O12,该材料在8 GPa的高压条件下合成,具有立方的晶格结构(Im¯3 空间群),在TCr=150 K和TMn=50 K附近依次发生反铁磁转变。理论计算预测两处反铁磁转变分别由B位Cr3+和Aʹ位Mn3+沿着111方向的G型共线反铁磁排列所致[81]。2015年,Wang等[9, 82]通过NPD证明了该磁结构,如图11所示。由于立方晶系结构的高对称性,LaMn3Cr4O12并不被预期具有多铁性。但是,随着温度降至50 K(Aʹ位Mn3+的反铁磁有序温度),LaMn3Cr4O12开始出现铁电极化,并且其介电常数、热释电电流(IP)以及电极化(P)均可被外加磁场(H)调控,如图12所示,其中E为极化电场。这一行为表明,LaMn3Cr4O12的铁电极化不仅具有磁性起源,而且存在着较强的磁电耦合。为了探索立方结构的LaMn3Cr4O12中由反铁磁序导致的铁电行为,考虑3种常见的磁电多铁微观机制[75]:首先是交换收缩模型(exchange striction model),其铁电极化来源于相邻自旋的数量积之和,且与自旋方向无关,但是理论计算表明,LaMn3Cr4O12的极化方向随着自旋在所有等效[111]方向上的变化而变化[9],因而不满足该模型;第2种微观机制是反DM模型(inverse DM model)或称为自旋流模型(spin current model),其铁电极化来源于相邻自旋间的矢量积,在具有G型反铁磁结构的LaMn3Cr4O12中,各自旋必然平行或反平行排列(图11),致使其矢量积始终为零,因此,该理论也无法解释其磁电多铁性;第3种是自旋依赖的p-d杂化模型(spin-dependent p-d hybridization model),这一模型通常用于解释具有特殊且复杂的自旋结构的材料中的铁电极化,如非共线的螺旋磁结构以及之字形(zigzag)的自旋链结构,因此,这一理论也不适用于具有高度对称结构的LaMn3Cr4O12。
尽管上述3种微观机制无法解释LaMn3Cr4O12磁电多铁性的成因,但是通过对称性分析发现,Cr3+和Mn3+子格分别属于−3ʹ和−3磁点群,两者均为非极化点群,但是,如果同时考虑2个子格共同的对称性,这2套磁子格共同构成极化的31′磁点群(图11),因此,可以打破空间反演对称性,诱导铁电极化。因此,LaMn3Cr4O12由于具有高度对称的晶体结构以及特殊的共线反铁磁结构,为多铁新机理研究提供了全新体系,并为多铁新材料探索与新机理研究开辟了新思路。
LaMn3Cr4O12所表现出的“出人意料的多铁性”[83]引起了研究者的广泛关注。Feng等[84]随即提出了一种新的微观机制以解释该新颖的磁电多铁性,称为各向异性的对称交换(anisotropic symmetric exchange)。考虑到LaMn3Cr4O12的电极化是由Mn3+和Cr3+的自旋共同诱导,因而它们的自旋相互作用是电极化产生的重要原因。由于Mn3+和Cr3+的次近邻原子均距离它们很远(大于6 Å),因此,最近邻的Mn3+-Cr3+相互作用是主要的考虑因素。理论计算中,材料的极化矩阵可写为Pint=PJ+PD+PΓ,其中:PJ为各向同性的对称对角矩阵(isotropic symmetric diagonal matrix),对应于交换收缩模型;PD为反对称矩阵(antisymmetric matrix),对应于自旋流模型;而PΓ为各向异性的对称交换矩阵。其中,当不考虑自旋-轨道耦合(spin-orbit coupling,SOC)时,PΓ的值为零,与密度泛函理论(density functional theory,DFT)计算结果[9]一致。在过去的研究中,通常不考虑PΓ,而在LaMn3Cr4O12中,Mn-Cr自旋对具有C1点群对称性,因而PΓ的每一个元素都可能不为零,因此,PΓ对电极化的贡献不可忽略。通过理论计算发现,PΓ具有有限值,并得到了沿[111]方向、大小为3.2×10−4 μC/cm2的电极化。这一结论也与DFT计算结果(3.4×10−4 μC/cm2)[9]一致。该研究还预言,随着SOC的加强,电极化也随之加强,因此,在一些5d过渡金属体系中,各向异性的对称交换作用对电极化的贡献可能超过其他电极化的产生机制。
尽管在LaMn3Cr4O12中发现了新的磁电耦合多铁性,但是其电极化(1.5×10−3 μC/cm2)很小,相比于Ⅰ类多铁性材料如BiFeO3(10~100 μC/cm2)低了几个数量级,即使相比于其他Ⅱ类多铁性材料如TbMnO3(0.08 μC/cm2)[70]和TbMn2O5(0.04 μC/cm2)[85],其电极化也弱了很多。对于具有6s2孤对电子的离子如Bi3+和Pb2+的Ⅰ类多铁性材料,由于电子云的极化,可能导致大的电极化的出现。如果结合Mn-Cr子格诱导的磁电多铁性,那么就可以同时实现大的电极化和磁-电相互调控。2017年,Zhou等[86]通过高压高温的合成方法成功制备了另一种新型A位有序四重钙钛矿BiMn3Cr4O12,其保持了LaMn3Cr4O12在TMn以下的磁电耦合多铁性,同时,由于将LaMn3Cr4O12中的A位La3+替换为具有6s2孤对电子的Bi3+离子,因而BiMn3Cr4O12在135 K附近由于Bi3+离子的6s2孤对电子的极化而发生了铁电相变,具有大的电极化(1.5 μC/cm2),比LaMn3Cr4O12提高了3个数量级。同时,BiMn3Cr4O12还具有大的磁电耦合系数(α=85 ps/m)。BiMn3Cr4O12不仅实现了较大的电极化,而且实现了磁电调控。因此,BiMn3Cr4O12实现了多种铁电相的共存,通过不同的极化过程实现了4种极化态,如图13所示[86–87],为多态磁电多铁性材料的探索与应用提供了新的思路。
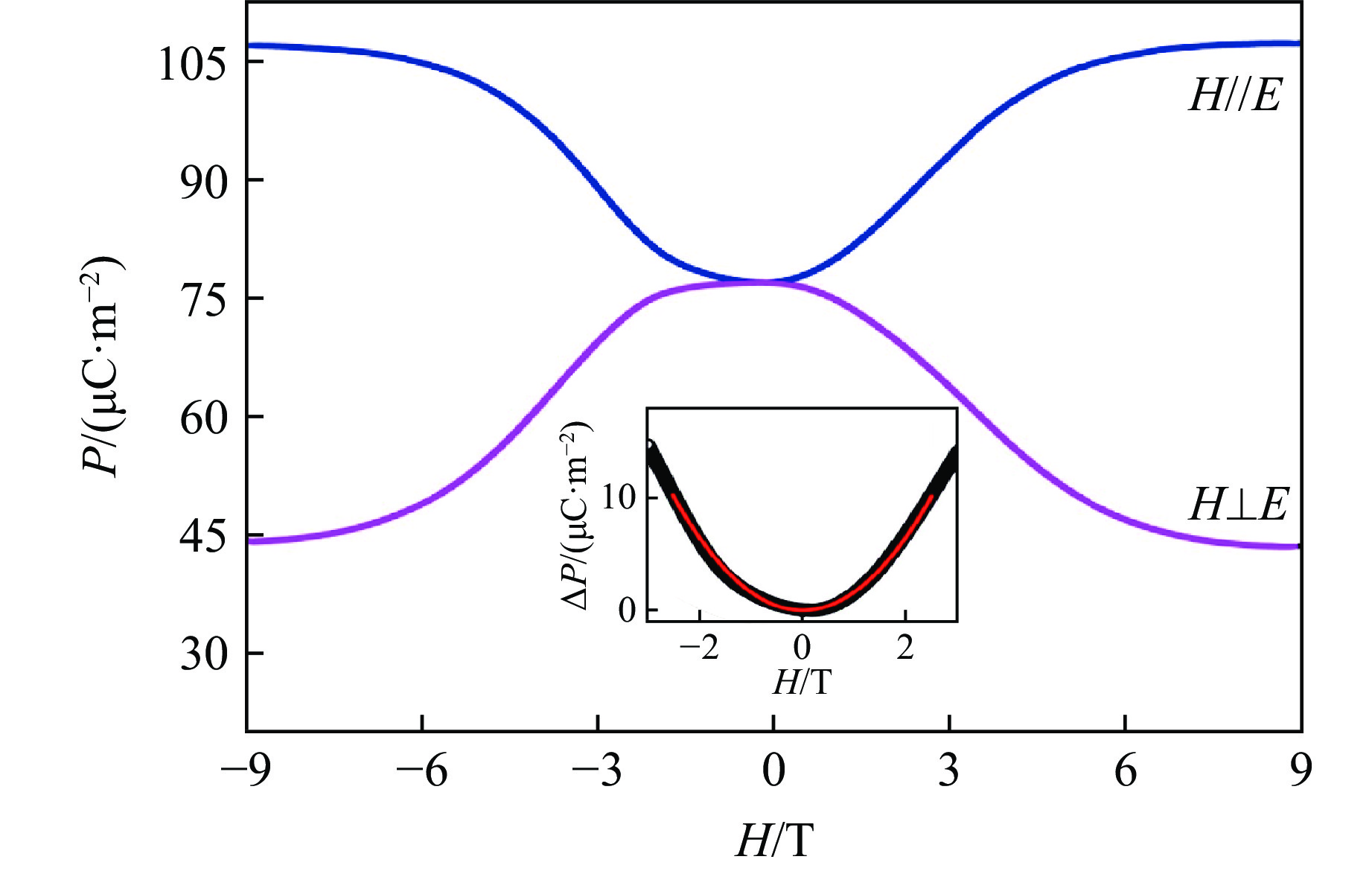
2021年,Liu等[88]指出,AMn3Cr4O12体系具有的31′磁点群仅允许偶数阶的磁电耦合效应,因此应具有强的二阶磁电效应,即当外加磁场与极化电场平行时,电极化显著增强,而当外加磁场与极化电场垂直时,电极化受到抑制。他们在SmMn3Cr4O12中测得了此效应,如图14所示,拟合得到二阶磁电系数β=d2P/dH2=2.56×10−18 s/A。目前,二阶磁电效应的物理机制还未被系统地阐述,因此,AMn3Cr4O12这一具有立方结构的钙钛矿体系为该领域的研究提供了重要的原型材料。
具有高对称性的A位有序四重钙钛矿氧化物还可能是研究材料拓扑结构的重要载体。二维拓扑流形可以分为可定向曲面和非定向曲面2种。可定向曲面包括球面和圆环面等,它们都有2个面,有内外之分;而非定向曲面,如莫比乌斯(Mobius)带、克莱因(Klein)瓶和罗马(Rome)面等,只有1个面,没有内外之分。一个常见且有趣的例子是克莱因瓶永远装不满水。因此,对于球面或圆环面,可以通过它们的贝里(Berry)曲率通量的量子化值来定义拓扑不变量,这对非定向曲面是不适用的。譬如,陈(Chern)绝缘体的底流形是圆环面,描述它们的拓扑不变量陈数就是该量子化值;外尔(Weyl)半金属中包裹外尔点的费米球是底流形,贝里曲率通量的量子化值就是其中外尔费米子的净磁荷数。非定向曲面另一个有趣的性质是,在面上沿着某闭合路径走一圈后,发现自己的左右对换,变成出发时镜子里的像。与定义在可定向曲面上的拓扑物态相比,非定向曲面的物理实现和物理性质的研究还比较少。如何在物理系统中实现非定向曲面,使得物理量在其上面的演化是一个非常值得研究的问题。由于非定向曲面独特的拓扑几何性质,在其上进行演化的物理量很可能呈现出一系列新奇的、路径依赖的物理现象。
莫比乌斯带是具有1条边界、1个面的二维曲面,可以通过排布或折叠纳米单晶或DNA带在三维实空间实现[89–90]。对于没有边界的、闭合的克莱因瓶和罗马面来说,它们在三维空间必定会自相交,因而它们在相空间的实现更容易。克莱因瓶可以看作是把2个莫比乌斯环的边界粘合在一起,而罗马面则是把莫比乌斯环和圆盘的边界粘合在一起。1844年,Steiner在罗马度假时发现并命名了罗马面[91],它的三维实现具有非常高的四面体Td对称性,存在4个三次对称轴以及自相交导致的双线(double line)、三重交点(triple point)和夹点(pinch point)等。可见,具有立方高对称性的晶格可能成为实现罗马面的最佳结构载体。
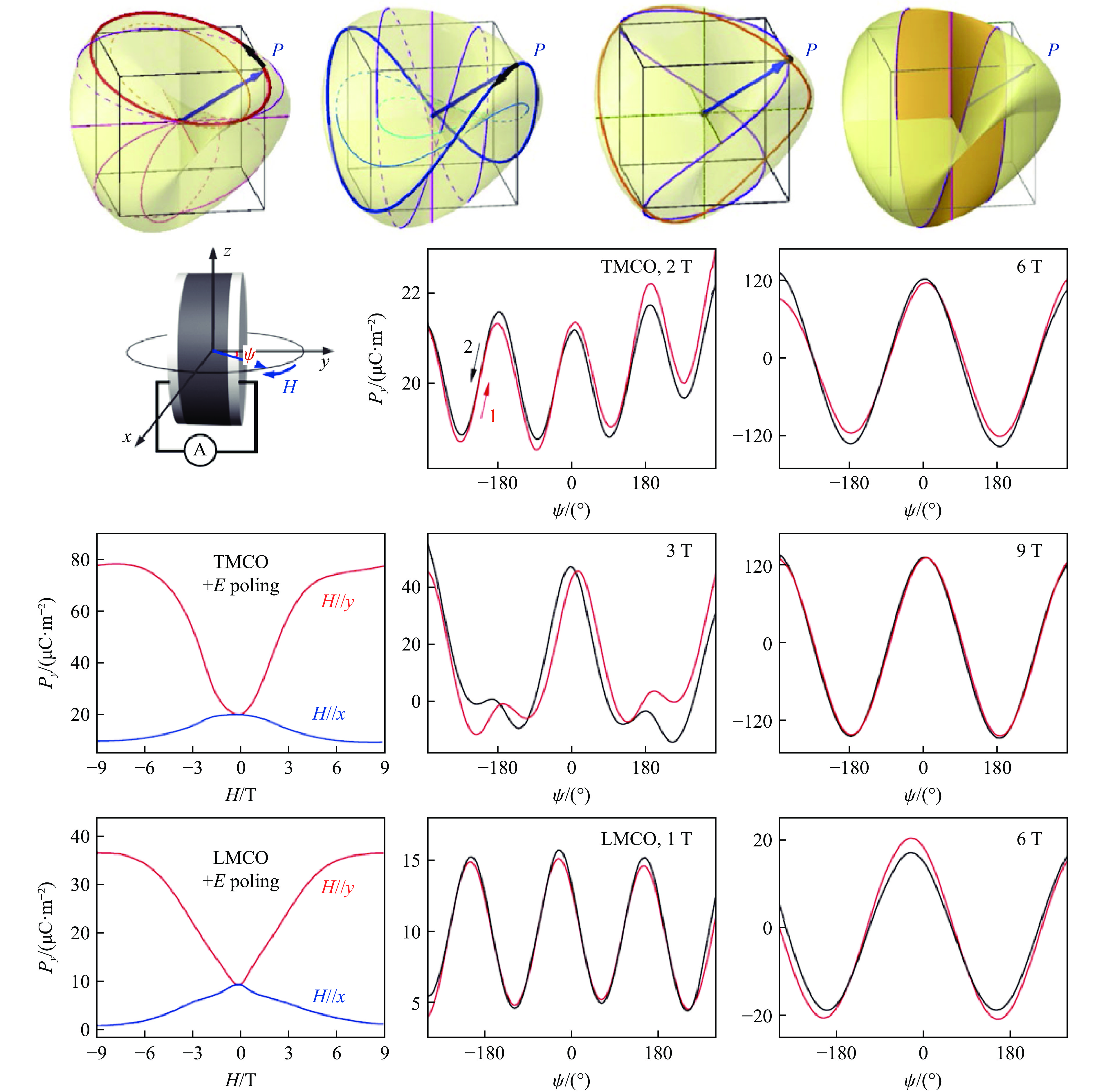
2022年,Liu等[92]通过研究LaMn3Cr4O12和TbMn3Cr4O12的电极化过程,首次观察到了非可定向罗马面的物理实现。理论计算表明,立方钙钛矿AMn3Cr4O12体系中自旋与电极化之间本征的磁电耦合作用使反铁磁自旋结构在三维空间转动时,电极化矢量在三维空间发生转动并组成了非定向的罗马面(图15)。该材料体系高对称的立方晶格与罗马面的四面体对称性兼容,是非常理想的实现体系。外加磁场可以控制奈尔矢量的转动,驱动磁诱导的电极化在罗马面上演化。当演化路径是罗马面上的非定向莫比乌斯带时,电极化转动的频率是奈尔矢量的2倍,即奈尔矢量转1圈,电极化在罗马面上运动2圈;当路径落在可定向圆盘上时,电极化的转动周期与奈尔矢量的转动周期相同。这种路径依赖的拓扑磁电响应表现出了罗马面的本征几何特性。实验上,通过控制不同大小的转动磁场对奈尔矢量转动模式调控,成功观测到了电极化与转动磁场之间不同的周期性依赖关系,如图15所示。近期,Wang等[93]通过第一性原理计算进一步证明了AMn3Cr4O12的自旋诱导铁电极化的演化路径在三维空间具有拓扑罗马面的形式。在AMn3Cr4O12立方钙钛矿多铁体系中,研究路径依赖的拓扑磁电效应有利于深入理解拓扑在数学和物理上的紧密关联,也为实现更多不可定向流形上的拓扑对象提供了新的思路。
2.4 高性能磁性半金属:ACu3Fe2Re2O12
材料中的电子具有2种自由度,分别为电荷自由度和自旋自由度。电荷自由度对应材料的电输运行为,决定其为金属、半导体或是绝缘体;而自旋自由度则对应于材料的磁性。传统的电子学认为,电子的电荷自由度和自旋自由度是分立的2种自由度:当考虑电荷自由度如电子在电场中的运动时,往往忽略其自旋自由度;而考虑自旋自由度如磁性时,又忽略其电荷自由度。长久以来,这种将电子的2种自由度拆分开来的观点在解释材料的物理性质上是可行且有效的。1988年,Baibich等[94]在Fe(001)/Cr(001)异质结中发现的巨磁电阻(giant magnetoresistance,GMR)打破了人们长久以来对电子的2种自由度的认知,实验发现,通过调控电子的自旋自由度,可以达到调控电子的电荷自由度的目的。因此,尽管Mott[95]在1936年就对自旋电子学(spintronics)进行了研究,这一学科至此才得到了广泛的关注和深入探索。
单相材料中的电荷自由度与自旋自由度相互关联的现象也被发现。在20世纪80年代,一系列Heusler合金表现出了奇异的电输运性质,根据施加于材料的电流的自旋方向的不同,这些Heusler合金表现出绝缘性或金属性。因此,这类材料被称为半金属铁磁体(half-metal ferromagnet,HMF)。HMF的能带示意图如图16(a)所示,其费米面穿过某一个自旋方向的能带,从而对该自旋方向的电子表现出金属性;而对于另一个自旋方向的能带,其费米面处于能隙之中,从而表现出绝缘性。因此,理论上,HMF在0 K时可以表现出100%的完全自旋极化。目前,对于HMF的探索主要集中于尖晶石结构AB2O4(如Fe3O4)、Heusler合金(如NiMnSb、Co2MnAl)以及二元氧化物CrO2等[96]。可以看到,由于HMF同时具有铁磁性和半金属性,因此,不仅需要磁性离子如过渡金属离子及其通过各种交换作用形成的长程磁有序,同时还需要足够复杂的晶格结构和电子相互作用,从而使不同自旋的能带劈裂开来。另外,还需要足够强的磁交换能,以克服泡利(Pauli)不相容原理所产生的电子间的相互作用势,才能使电子完全占据在同一自旋方向的能带上。
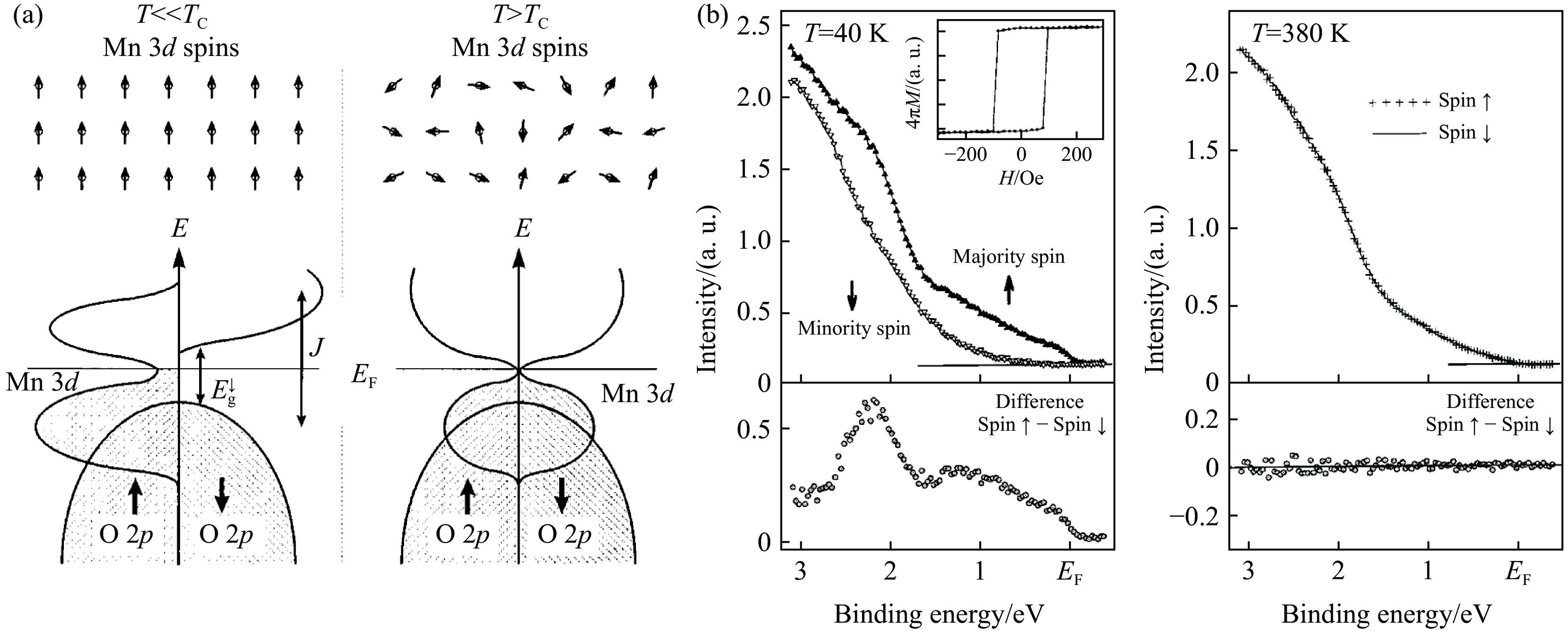
对于HMF形成所要求的复杂多样的条件,容易想到钙钛矿尤其是A位有序四重钙钛矿氧化物是理想的候选材料。钙钛矿容纳各种离子的灵活性及其复杂的晶体结构为HMF的发现提供了充分的结构基础,也为HMF开辟了新的研究领域。1998年,Park等[97]通过自旋分辨光电子能谱(spin-resolved photoemission)首次在ABO3型钙钛矿La0.7Sr0.3MnO3薄膜中观察到了HMF行为,如图16(b)所示,La0.7Sr0.3MnO3的半金属行为与其铁磁性密切相关,La0.7Sr0.3MnO3中的3d过渡金属Mn表现出了2种化合价Mn3+(
t32ge1g )和Mn4+(t32g ),2种Mn离子通过eg轨道电子的双交换作用形成铁磁序。同时,双交换作用产生了一个很大的磁交换能J(约2.5 eV),远远大于eg能带的宽度(约1 eV),因此自旋向下的能带在费米面处打开了一个能隙Eg,半金属性由此产生,如图16(a)所示。Hwang等[98]在La0.7Sr0.3MnO3多晶中观察到GMR行为,并指出此GMR来源于半金属晶界间的自旋极化隧穿(spin-polarized tunneling)效应。在La0.7Sr0.3MnO3中,2种具有不同电荷/自旋组态的Mn3+(
t32ge1g )和Mn4+(t32g )同时占据B位,它们之间的双交换作用导致了La0.7Sr0.3MnO3的半金属行为。如果材料的晶体结构具有更多的容纳过渡金属离子的位置,或许可以发现更多的半金属材料。而在双钙钛矿A2BB′O6中,B位和B′位可以分别容纳不同的过渡金属离子,为更多半金属材料的发现提供了机遇。Kobayashi等[99]通过理论计算发现双钙钛矿Sr2FeMoO6是半金属,其B位Fe3+与B′位Mo5+在TC(约420 K)附近通过超交换作用形成亚铁磁结构。Sr2FeMoO6的磁阻也表现出GMR行为,如图17所示,当温度远低于其TC时,磁阻随着磁场的变化产生了弛豫行为,并呈现蝴蝶形(butterfly-shaped)磁阻曲线,其峰值正好对应其矫顽场Hc。Sr2FeMoO6产生蝴蝶形磁阻的原因如下:当磁场强度降至−Hc时,材料的磁化强度降至零,对应于体系的磁矩最混乱无序的状态,此时体系的磁散射最强,因此,电阻最大;当磁场继续下降,材料的磁矩被磁场逐渐扭转到平行于磁场的方向,在此过程中,对于自旋方向与磁场相同的电荷,磁矩的散射逐渐减弱,因而电阻下降。此外,在另一种双钙钛矿Sr2FeReO6中也发现了类似的磁阻行为,预示着半金属性的存在[100]。对于A位有序四重钙钛矿氧化物,由于其能容纳更多的磁性离子,其中的相互作用更加丰富和复杂,理论研究变得更加困难,同时由于其通常需要高压手段进行合成,在A位有序四重钙钛矿氧化物中对半金属材料的探索长期以来没有取得进展。直到2014年,Chen等[12]首次发现了具有半金属性的CaCu3Fe2Re2O12,其具有形如
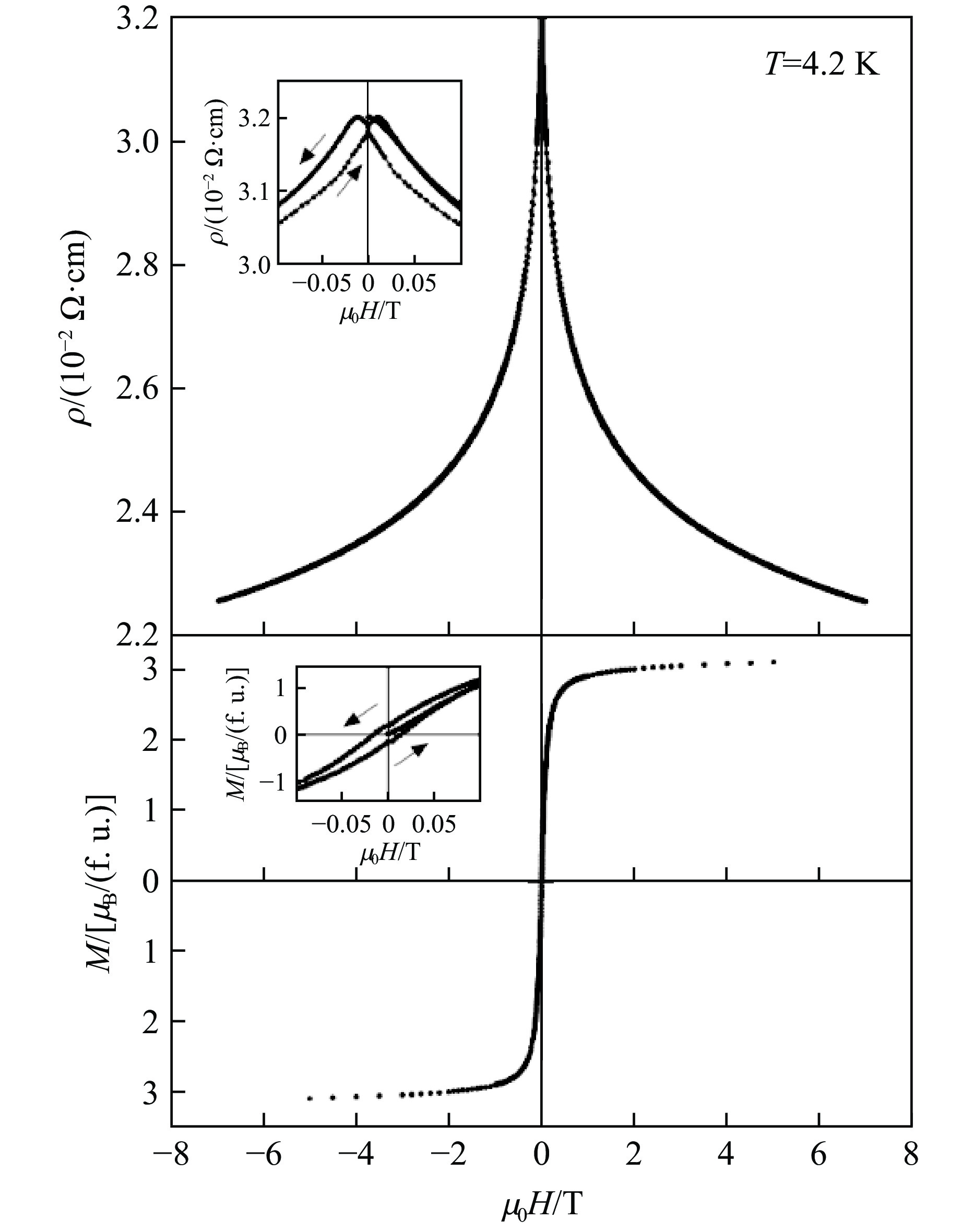
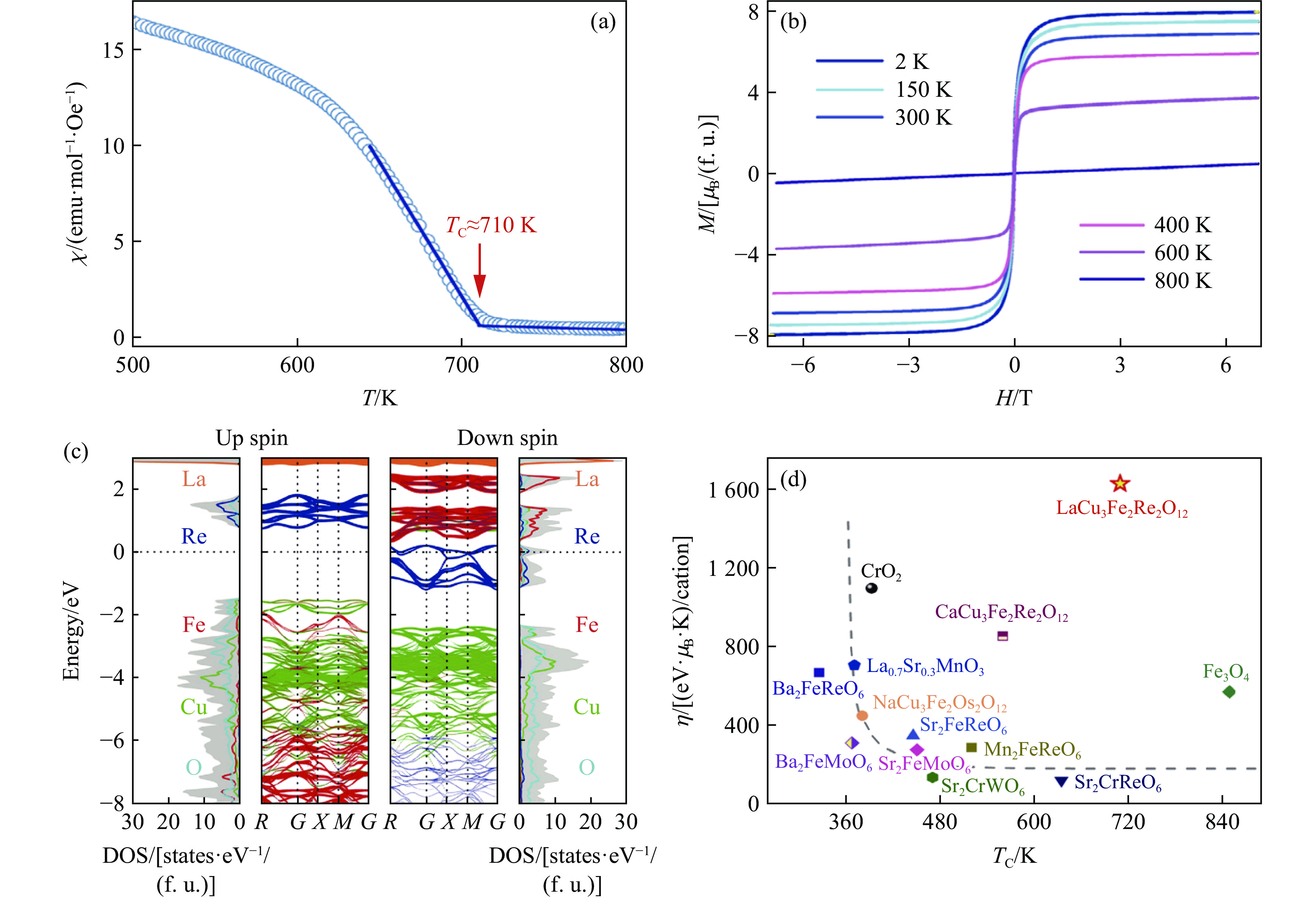
AA′3B2B′2O12 的A、B位同时有序的四重钙钛矿结构,其中B位的Fe和B′位的Re形成岩盐有序结构,在TC 约560 K时,其A位Cu2+和B位Fe3+的磁矩平行排列,并与B′位Re5+的磁矩反平行排列,形成亚铁磁有序,如图18(a)所示。CaCu3Fe2Re2O12的低温磁阻测量表明,其在弱磁场下的电阻随磁场的增强而迅速减小,表现出GMR行为,同时,其磁阻随磁场的变化也出现滞后现象,形成蝴蝶形磁阻曲线,预示着其半金属性同样来源于自旋极化的隧穿效应,如图18(b)所示。理论计算表明,CaCu3Fe2Re2O12具有半金属的能带结构,如图18(c)所示,该材料自旋向上的能带在费米面附近具有宽度约1.2 eV的能隙,而自旋向下的能带在费米面附近没有能隙。从图18(b)还可以发现,CaCu3Fe2Re2O12的磁阻曲线的峰值并不位于Hc处,而从图18(b)的插图可以看到,CaCu3Fe2Re2O12的电阻随温度下降而缓慢上升,而不是金属常见的电阻随温度下降而下降,这一行为可能源于多晶材料的晶粒间界效应,较大的晶粒间界也可能是导致电阻曲线的峰值与Hc不一致的原因之一。另外,B位和B′位离子的反占位也有可能破坏理想的半金属能带结构,从而使磁阻行为与理想的半金属出现偏差。CaCu3Fe2Re2O12使半金属研究首次深入此类复杂的钙钛矿氧化物中,由此开始了对A位有序四重钙钛矿氧化物的半金属性的探索。2022年,Liu等[101]报道了另一种新型A位有序四重钙钛矿LaCu3Fe2Re2O12,其TC高达710 K,如图19所示,创造了钙钛矿半金属TC的新纪录。其高TC可用海森堡(Heisenberg)模型
H=∑ijJijSi×Sj 解释:理论计算表明,LaCu3Fe2Re2O12的磁性由Cu/Fe与Re之间的反铁磁耦合主导,从而形成Cu(↑)Fe(↑)Re(↓)的自旋组态[101–104],因此,若能提高其哈密顿(Hamilton)量H,则可预期更高的TC。相比于CaCu3Fe2Re2O12,LaCu3Fe2Re2O12的A位由Ca2+变为La3+,导致B位Re的价态由Re5+(5d2,S=1)降低至Re4.5+(5d2.5,S=2.5/2),增加了自旋角动量S,从而使TC提高。此外,LaCu3Fe2Re2O12还具有高达Ms=8.0μB/(f. u.)的饱和磁矩,理论计算还得到了Eg=2.3 eV的上自旋宽能隙。因此,如果定义半金属综合性能指标η=TCEgMs,如图19所示,那么在TC高于室温的半金属氧化物中,LaCu3Fe2Re2O12具有半金属氧化物中最高的综合性能。LaCu3Fe2Re2O12的制备与研究提供了一个高性能磁性半金属的范例,为探索具有实际应用前景的半金属材料提供了新的思路。 图 19 LaCu3Fe2Re2O12的 (a) 磁化率随温度的变化曲线、(b) 磁化强度随磁场的变化曲线、(c) 能带计算结果以及 (d) 半金属综合性能指标η与其他半金属氧化物的比较[101]Figure 19. (a) Temperature-dependent magnetic susceptibility, (b) field-dependent magnetization, (c) calculated band structure from first principles and (d) overall performance factor η of LaCu3Fe2Re2O12 (The η values of some selected half-metallic oxides are displayed for comparison.)[101]
图 19 LaCu3Fe2Re2O12的 (a) 磁化率随温度的变化曲线、(b) 磁化强度随磁场的变化曲线、(c) 能带计算结果以及 (d) 半金属综合性能指标η与其他半金属氧化物的比较[101]Figure 19. (a) Temperature-dependent magnetic susceptibility, (b) field-dependent magnetization, (c) calculated band structure from first principles and (d) overall performance factor η of LaCu3Fe2Re2O12 (The η values of some selected half-metallic oxides are displayed for comparison.)[101]根据上述海森堡模型,可以预见,如果继续降低Re的价态,则有可能进一步提高这一半金属材料体系的TC。近期,本课题组还制备出了氧缺位的A位有序四重钙钛矿LaCu3Fe2Re2O12−δ,进一步使Re的价态降低至Re4+(5d3,S=3/2),从而将其TC提升至760 K。同时,理论计算结果表明其为半金属,并具有2.48 eV的上自旋宽能隙。LaCu3Fe2Re2O12−δ是迄今为止具有最高TC的钙钛矿半金属。
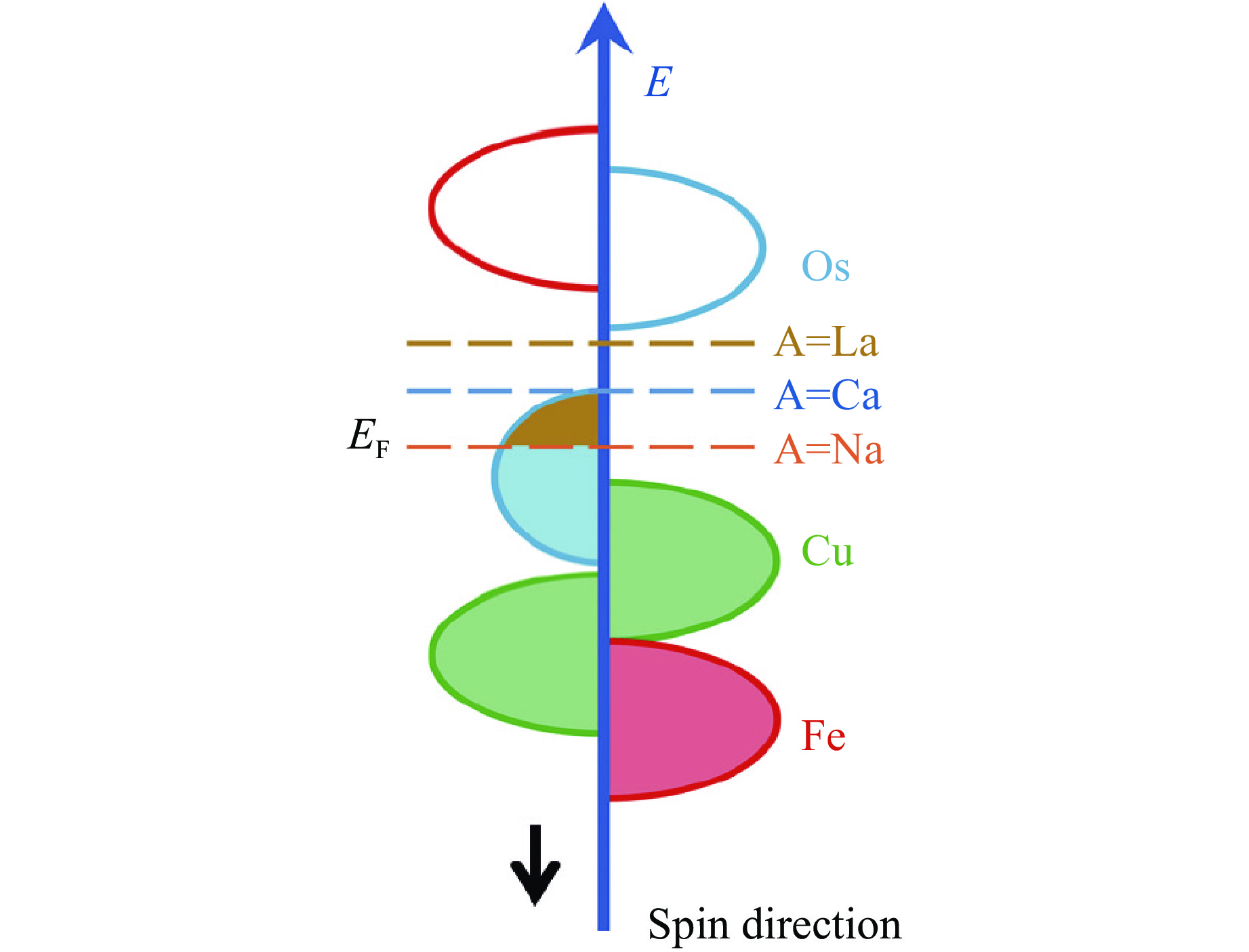
除了ACu3Fe2Re2O12体系以外,半金属性还广泛地存在于A位有序四重钙钛矿氧化物中。例如,LaCu3Co2Re2O12在2 K、8 T的磁阻可达到7%,但其TC较低(150 K)[105]。而NaCu3Fe2Os2O12是首个被报道的Fe-Os体系钙钛矿半金属,具有室温以上的TC(380 K)[106]。不同的是,当A位Na+替换为更高价态的Ca2+和La3+,该材料将会转变成为半导体[10, 107]。Ye等[108]通过比较这一ACu3Fe2Os2O12体系的能带结构指出,A位离子尽管不具有磁性,但可以有效地调节材料的费米面,从而可以有目的地调控材料,以实现金属、半金属、半导体以及绝缘体性质,如图20所示。需要指出的是,CaCu3Fe2Os2O12的能带结构预示着其为双极磁性半导体(价带顶和导带底具有100%的自旋极化,且两者的自旋极化方向相反)[109],与半金属同属重要的自旋电子学材料。因此,A位有序四重钙钛矿氧化物以其丰富多变的离子组合、复杂的磁相互作用,成为探索高性能半金属性以及高TC磁性材料的重要材料体系,在未来的自旋电子学器件、高温磁体等领域具有可观的应用潜力。
3. 结论与展望
A位有序四重钙钛矿氧化物以其独特的晶体结构和丰富多彩的物理性质,近20年来作为研究热点受到了广泛的关注,取得了长足的发展。相比于简单的ABO3型钙钛矿,A位有序四重钙钛矿氧化物中3/4的A位非磁性离子被过渡金属离子A′取代,形成了1∶3的A/A′有序结构。因此,A位有序四重钙钛矿氧化物中的磁-电相互作用不再仅仅局限于B子格内部(如B-B),新颖的磁-电相互作用如A′-A′和A′-B也随之产生。迄今为止,由于A′位磁性离子的引入,A位有序四重钙钛矿氧化物表现出了极为丰富的物理性质,如高介电常数、负热膨胀、电荷有序、磁电多铁性、高性能半金属性等,因此,具有重要的基础研究价值和可观的应用前景。值得注意的是,由于A位有序四重钙钛矿氧化物的A′位由较小的过渡金属占据,因此,需要足够高的外部压力使之与配位的O足够接近从而形成化学键。另一方面,小的A′位过渡金属离子还会使B/B′O6八面体发生严重的倾斜,其典型的B―O―B′键角由理想的180°减小至140°左右。巨大的晶格畸变导致此类材料的常压制备异常困难,高压制备方法为A位有序四重钙钛矿氧化物的研究提供了机会。
人类对材料中电荷自由度的充分利用,促成了大规模集成电路的产生,极大地促进了现代文明的发展。自发现巨磁阻效应以来,科学家们通过探索电子的内禀自旋属性为操纵电子提供新的自由度,发现了一系列新奇效应,奠定了第三次产业革命的基础,引领整个人类社会进入新型信息时代。半金属材料作为自旋注入源[110],A位有序四重钙钛矿氧化物为寻找具有高温稳定性、高自旋极化率、抗干扰能力强的半金属材料提供了新的材料体系。另一方面,在未来的非易失的磁电随机存储器(magnetoelectric random access memory,MeRAM)中,磁电多铁性材料是其关键组成部分。目前,研究者已通过Ⅰ类多铁性材料BiFeO3的压电/压磁性质实现对CoFe外延磁性层一定程度的磁-电调控[77]。若寻找到能够实现此功能的单相Ⅱ类多铁性材料,则可极大地减少能量损耗,并提高响应速度。其中,A位有序四重钙钛矿氧化物具有丰富且强的磁-电相互作用,是探索大铁电极化、强磁电耦合、低矫顽场、快响应的磁电多铁性材料的重要材料体系。此外,大体积单晶生长和高质量的异质结外延也是A位有序四重钙钛矿氧化物通往实际应用的重要攻坚方向。
清洁能源和碳中和是当代的重要主题,在寻求清洁、高效的可持续新能源之路上,氢能被寄予厚望。然而,氢能利用长期受限于析氧反应效率,研发高效、稳定、绿色的电催化剂或者寻求新的突破点成为该领域亟待解决的问题。近年来,研究人员发现,ABO3钙钛矿具有良好的电化学活性,特别是其衍生结构A位有序四重钙钛矿
AA′3B4O12 在电解水中的催化性能显著增强,并且该结构也为减少贵金属含量甚至非贵金属催化剂提供了一种有效方案[13, 111–112]。鉴于A′位磁性离子对材料性能的显著提升,如果把A位有序四重钙钛矿氧化物中剩余1/4的A位也替换为磁性过渡金属离子,全过渡金属(transition-metal-only)A位有序四重钙钛矿氧化物由于其A、A′、B和B′位均被磁性过渡金属离子所占据,将具有更加丰富的磁-电相互作用(如图21所示),由此产生更多新颖的物性,并进一步提高材料的性能。例如,MnCu3V4O12[113]和CuCu3V4O12[114]在低温下表现出奇异的比热行为,进一步的研究表明,这一行为来自A位较小的磁性离子(Mn2+、Cu2+)在AO12笼子中的振动。此外,A位Mn2+离子的引入也使CaCu3Mn4O12的TC由355 K进一步提高至MnCu3Mn4O12的365 K。有趣的是,对二元氧化物Mn2O3在约20 GPa的高压下处理,可以形成具有A位有序四重钙钛矿结构的ζ-Mn2O3相(
Mn2+Mn3+3Mn3.25+4O12 ,图9(b))[67],并在其中发现了新颖的磁电多铁性,其原因在于多种磁性格点间复杂的磁相互作用导致螺旋磁结构的形成,其磁电多铁性可以被自旋流模型所解释[115]。类似地,有迹象表明,Fe2O3在高压下(约50 GPa)也出现了具有A位有序四重钙钛矿结构的ζ-Fe2O3相(图9(c))[68]。这些发现也为矿物研究和地球物理研究提供了思路。然而,迄今为止,受实验技术的限制,对全过渡金属A位有序四重钙钛矿氧化物的报道极少。随着高压合成手段的发展,全过渡金属A位有序四重钙钛矿氧化物可以为高压技术、物性探索以及交叉学科的研究开辟广阔的空间。与此同时,A位有序四重钙钛矿氧化物的研究还存在许多亟待解决的问题。在材料制备方面,理论预测的许多新的材料体系[3, 116–117]以及高压下大块高质量单晶生长的迫切需求,均对实验合成条件和工艺探索提出了新的挑战和机遇。在物理性质方面,许多A位有序四重钙钛矿氧化物的性质研究还存在诸多难点,例如:AMn3Mn4O12(A=Na, Ca, Sr, Cd, Pb, Mn, Hg)这一体系具有的复杂多变的磁结构[118–120];对于
ACu3Fe2B′2O12 (A=Na, Ca, La;Bʹ=Re, Os),尽管理论计算和间接的实验证据均表明其为半金属材料[12, 101, 106],但仍缺乏直接的实验证据;A位有序四重钙钛矿氧化物在电解水过程中的催化机制仍存在争议[13, 111–112]。因此,A位有序四重钙钛矿氧化物以其灵活的组分、多样的物性以及丰富的物理内涵,成为材料科学和物理学重要的材料体系,可以预期,未来人们将在其中探索出更多的新材料和新物理。 -
图 2 (a) Aʹ的氧配位示意图(黄色表示Aʹ离子,红色表示O离子,颜色由深至浅表示Aʹ―O键长由短至长),(b) AʹO4平面四边形晶体场示意图(10Dq为d轨道(t2g、eg)的劈裂,Δt2g、Δeg分别为t2g(xy、xz、yz)和eg(x2–y2、z2–r2)轨道的劈裂),(c) BO6八面体的倾斜(蓝色表示B离子,红色表示O离子)
Figure 2. (a) Coordination of the Aʹ site, the Aʹ ion is displayed in yellow, the O anions are displayed in red, and the different colors of O indicate the different Aʹ―O bond lengths; (b) crystal field of AʹO4 square planar, the 10Dq represents the split of the d orbit (t2g, eg), the Δt2g and Δeg represent the split of the t2g (xy, xz, yz) and eg (x2–y2, z2–r2) orbits, respectively; (c) tilt of the BO6 octahedra, the B ions are displayed in blue, and the O anions are displayed in red
图 3 (a) CaCu3Ti4O12的εʹ和tan δ随温度的变化关系(2条曲线分别为2个样品的测试数据)[27];(b) 不同频率下εʹ、tan δ和ω0随温度的变化关系[27];(c) εʹ随频率的变化关系;(d) 弛豫时间(τ)随温度的变化关系(10 K的τ为预测值)[29]
Figure 3. (a) Temperature-dependent εʹ and tan δ of two CaCu3Ti4O12 samples[27]; (b) temperature-dependent εʹ, tan δ and ω0 at selected frequencies[27]; (c) frequency-dependent εʹ of CaCu3Ti4O12 and (d) the relaxation time (τ) as a function of 1/T, the legend also gives the estimated τ at 10 K[29]
图 6 LaCu3Fe4O12在TN=393 K的多种转变:(a) Cu―O键、Fe―O键的键长随温度的变化关系;(b) 体积随温度的变化关系;(c) 穆斯堡尔(Mössbauer)谱的光吸收随运动速度的变化关系;(d) 磁化率(χ)和电阻率(ρ)随温度的变化曲线(插图为磁矩M随温度的变化曲线)[7]
Figure 6. Multiple transitions of LaCu3Fe4O12 at TN=393 K: (a) temperature-dependent Cu―O and Fe―O bond lengths; (b) temperature-dependent negative thermal expansion; (c) Mössbauer spectra, the velocity-dependent absorption; (d) temperature-dependent magnetic susceptibility (χ) and resistivity (ρ), the inset displays the temperature-dependent magnetization (M)[7]
图 7 (a) LnCu3Fe4O12的电荷有序形式总览;(b) LnCu3Fe4O12在相变温度附近的体积随温度的变化曲线;(c) Ln和Fe的键合状态(d为价键求和(bond valence sum,BVS)计算得到的价态与自由离子价态之差,d < 0表示欠键合,d > 0表示过键合)[61]
Figure 7. (a) An overview of charge order of LnCu3Fe4O12; (b) temperature-dependent volume of LnCu3Fe4O12; (c) correlation between dLn and dFe (d is the difference between bond valence sum (BVS) and ionic valence state. d < 0 indicates underbonding and d > 0 indicates overbonding.)[61]
图 8 (a) ACu3Fe4O12体系电荷有序能级示意图[62];(b) 当体积为原体积的102%、100%、96%、90%、88%、80%、78%时的电荷分布(不同颜色表示不同位置电荷相对密度差异Δn(r))[63]
Figure 8. (a) Schematic diagram of charge order in the ACu3Fe4O12 compounds[62]; (b) computed charge densities for volumes of 102%, 100%, 96%, 90%, 88%, 80% and 78%, the colors represent the charge density differences Δn(r)[63]
图 19 LaCu3Fe2Re2O12的 (a) 磁化率随温度的变化曲线、(b) 磁化强度随磁场的变化曲线、(c) 能带计算结果以及 (d) 半金属综合性能指标η与其他半金属氧化物的比较[101]
Figure 19. (a) Temperature-dependent magnetic susceptibility, (b) field-dependent magnetization, (c) calculated band structure from first principles and (d) overall performance factor η of LaCu3Fe2Re2O12 (The η values of some selected half-metallic oxides are displayed for comparison.)[101]
-
[1] CARPENTER M A, HOWARD C J. Symmetry rules and strain/order-parameter relationships for coupling between octahedral tilting and cooperative Jahn-Teller transitions in ABX3 perovskites. Ⅰ. theory [J]. Acta Crystallographica Section B, 2009, 65(Pt 2): 134−146. [2] CARPENTER M A, HOWARD C J. Symmetry rules and strain/order-parameter relationships for coupling between octahedral tilting and cooperative Jahn-Teller transitions in ABX3 perovskites. Ⅱ. application [J]. Acta Crystallographica Section B, 2009, 65(Pt 2): 147−159. [3] VASALA S, KARPPINEN M. A2BʹBʹʹO6 perovskite: a review [J]. Progress in Solid State Chemistry, 2015, 43(1/2): 1–36. [4] ANDERSON P W. More is different: broken symmetry and the nature of the hierarchical structure of science [J]. Science, 1972, 177(4047): 393–396. doi: 10.1126/science.177.4047.393 [5] DESCHANVRES A, RAVEAU B, TOLLEMER F. Substitution of copper for a divalent metal in perovskite-type titanates [J]. Bulletin de la Société Chimique de France, 1967, 11: 4077–4078. [6] SUBRAMANIAN M A, LI D, DUAN N, et al. High dielectric constant in ACu3Ti4O12 and ACu3Ti3FeO12 phases [J]. Journal of Solid State Chemistry, 2000, 151(2): 323–325. doi: 10.1006/jssc.2000.8703 [7] LONG Y W, HAYASHI N, SAITO T, et al. Temperature-induced A-B intersite charge transfer in an A-site-ordered LaCu3Fe4O12 perovskite [J]. Nature, 2009, 458(7234): 60–63. doi: 10.1038/nature07816 [8] ZHAO J F, GAO J C, LI W M, et al. A combinatory ferroelectric compound bridging simple ABO3 and A-site-ordered quadruple perovskite [J]. Nature Communications, 2021, 12(1): 747. doi: 10.1038/s41467-020-20833-6 [9] WANG X, CHAI Y S, ZHOU L, et al. Observation of magnetoelectric multiferroicity in a cubic perovskite system: LaMn3Cr4O12 [J]. Physical Review Letters, 2015, 115(8): 087601. doi: 10.1103/PhysRevLett.115.087601 [10] DENG H S, LIU M, DAI J H, et al. Strong enhancement of spin ordering by A-site magnetic ions in the ferrimagnet CaCu3Fe2Os2O12 [J]. Physical Review B, 2016, 94(2): 024414. doi: 10.1103/PhysRevB.94.024414 [11] ZENG Z, GREENBLATT M, SUBRAMANIAN M A, et al. Large low-field magnetoresistance in perovskite-type CaCu3Mn4O12 without double exchange [J]. Physical Review Letters, 1999, 82(15): 3164–3167. doi: 10.1103/PhysRevLett.82.3164 [12] CHEN W T, MIZUMAKI M, SEKI H, et al. A half-metallic A- and B-site-ordered quadruple perovskite oxide CaCu3Fe2Re2O12 with large magnetization and a high transition temperature [J]. Nature Communications, 2014, 5: 3909. doi: 10.1038/ncomms4909 [13] YAGI S, YAMADA I, TSUKASAKI H, et al. Covalency-reinforced oxygen evolution reaction catalyst [J]. Nature Communications, 2015, 6: 8249. doi: 10.1038/ncomms9249 [14] OVSYANNIKOV S V, ZAINULIN Y G, KADYROVA N I, et al. New antiferromagnetic perovskite CaCo3V4O12 prepared at high-pressure and high-temperature conditions [J]. Inorganic Chemistry, 2013, 52(20): 11703–11710. doi: 10.1021/ic400649h [15] PATINO M A, ROMERO F D, GOTO M, et al. Multi- k spin ordering in CaFe3Ti4O12 stabilized by spin-orbit coupling and further-neighbor exchange [J]. Physical Review Research, 2021, 3(4): 043208. doi: 10.1103/PhysRevResearch.3.043208 [16] BOCHU B, DESCHIZEAUX M N, JOUBERT J C, et al. Synthèse et caractérisation d'une série de titanates pérowskites isotypes de [CaCu3](Mn4)O12 [J]. Journal of Solid State Chemistry, 1979, 29(2): 291–298. doi: 10.1016/0022-4596(79)90235-4 [17] MAREZIO M, DERNIER P D, CHENAVAS J, et al. High pressure synthesis and crystal structure of NaMn7O12 [J]. Journal of Solid State Chemistry, 1973, 6(1): 16–20. doi: 10.1016/0022-4596(73)90200-4 [18] BOCHU B, CHENAVAS J, JOUBERT J C, et al. High pressure synthesis and crystal structure of a new series of perovskite-like compounds CM7O12 (C=Na, Ca, Cd, Sr, La, Nd) [J]. Journal of Solid State Chemistry, 1974, 11(2): 88–93. doi: 10.1016/0022-4596(74)90102-9 [19] CHENAVAS J, JOUBERT J C, MAREZIO M, et al. The synthesis and crystal structure of CaCu3Mn4O12: a new ferromagnetic-perovskite-like compound [J]. Journal of Solid State Chemistry, 1975, 14(1): 25–32. doi: 10.1016/0022-4596(75)90358-8 [20] OZAKI Y, GHEDIRA M, CHENAVAS J, et al. High-pressure synthesis and bond lengths of calcium copper germanium oxide [CaCu3](Ge4)O12 [J]. Acta Crystallographica, 1977, B33: 3615–3617. [21] MEYER C, GROS Y, BOCHU B, et al. Synthesis, crystal structure, and Mössbauer study of a series of perovskite-like compounds [ACu3](M, Fe)4O12 [J]. Physica Status Solidi (A), 1978, 48(2): 581–586. doi: 10.1002/pssa.2210480239 [22] BOCHU B, JOUBERT J C, COLLOMB A, et al. Ferromagnetic oxides [Ln3+/Cu3]Mn4O12 (Ln=La to Lu and Y) [J]. Journal of Magnetism and Magnetic Materials, 1980, 15: 1319–1321. [23] BRYNTSE I, WERNER P E. Synthesis and structure of a perovskite related oxide, Bi2/3Cu3Ti4O12 [J]. Materials Research Bulletin, 1990, 25(4): 477–483. doi: 10.1016/0025-5408(90)90183-3 [24] LEINENWEBER K, LINTON J, NAVROTSKY A, et al. High-pressure perovskites on the joint CaTiO3-FeTiO3 [J]. Physics and Chemistry of Minerals, 1995, 22(4): 251–258. [25] TROYANCHUK I O, LOBANOVSKY L S, KASPER N V, et al. Magnetotransport phenomena in A(Mn3− x Cu x )Mn4O12 (A=Ca, Tb, Tm) perovskites [J]. Physical Review B, 1998, 58(22): 14903–14907. doi: 10.1103/PhysRevB.58.14903 [26] ZENG Z, GREENBLATT M, SUNSTROM J E, et al. Giant magnetoresistance in CaCu3Mn4O12-based oxides with perovskite-type structure [J]. Journal of Solid State Chemistry, 1999, 147(1): 185–198. doi: 10.1006/jssc.1999.8212 [27] RAMIREZ A P, SUBRAMANIAN M A, GARDEL M, et al. Giant dielectric constant response in a copper-titanate [J]. Solid State Communications, 2000, 115(5): 217–220. doi: 10.1016/S0038-1098(00)00182-4 [28] CHOUDHARY R N P, BHUNIA U. Structural, dielectric and electrical properties of ACu3Ti4O12 (A=Ca, Sr, and Ba) [J]. Journal of Materials Science, 2002, 37(24): 5177–5182. doi: 10.1023/A:1021019412533 [29] HOMES C C, VOGT T, SHAPIRO S M, et al. Optical response of high-dielectric-constant perovskite-related oxide [J]. Science, 2000, 293(5530): 673–676. [30] HE L X, NEATON J B, COHEN M H, et al. First-principles study of the structure and lattice dielectric response of CaCu3Ti4O12 [J]. Physical Review B, 2002, 65(21): 214112. doi: 10.1103/PhysRevB.65.214112 [31] COLLOMB A, SAMARAS D, BOCHU B, et al. Propriétés et structure magnétiques de CaCu3Ti4O12 à structure perovskite [J]. Physica Status Solidi A, 1977, 41(2): 459–463. doi: 10.1002/pssa.2210410215 [32] KOITZSCH A, BLUMBERG G, GOZAR A, et al. Antiferromagnetism in CaCu3Ti4O12 studied by magnetic Raman spectroscopy [J]. Physical Review B, 2002, 65(5): 052406. doi: 10.1103/PhysRevB.65.052406 [33] LUNKENHEIMER P, BOBNAR V, PRONIN A V, et al. Origin of apparent colossal dielectric constants [J]. Physical Review B, 2002, 66(5): 052105. [34] MAXWELL J C. A Treatise on electricity and magnetism [M]. 3rd ed. New York: Dover, 1954. [35] WAGNER K W. Zur theorie der unvollkommenen dielektrika [J]. Annalen der Physik, 1913, 345(5): 817–855. doi: 10.1002/andp.19133450502 [36] LARSEN P K, METSELAAR R. Electric and dielectric properties of polycrystalline yttrium iron garnet: space-charge-limited currents in an inhomogeneous solid [J]. Physical Review B, 1973, 8(5): 2016–2025. doi: 10.1103/PhysRevB.8.2016 [37] TSELEV A, BROOKS C M, ANLAGE S M et al. Evidence for power-law frequency dependence of intrinsic dielectric response in the CaCu3Ti4O12 [J]. Physical Review B, 2004, 70(14): 144101. doi: 10.1103/PhysRevB.70.144101 [38] LIU J J, DUAN C G, YIN W G, et al. Large dielectric constant and Maxwell-Wagner relaxation in Bi2/3Cu3Ti4O12 [J]. Physical Review B, 2004, 70(14): 144106. doi: 10.1103/PhysRevB.70.144106 [39] LIU J J, DUAN C G, MEI W N. Dielectric properties and Maxwell-Wagner relaxation of compounds ACu3Ti4O12 (A=Ca, Bi2/3, Y2/3, La2/3) [J]. Journal of Applied Physics, 2005, 98(9): 093703. doi: 10.1063/1.2125117 [40] SHAO S F, ZHANG J L, ZHENG P, et al. Microstructure and electrical properties of CaCu3Ti4O12 ceramics [J]. Journal of Applied Physics, 2006, 99(8): 084106. doi: 10.1063/1.2191447 [41] FU D S, TANIGUCHI H, TANIYAMA T, et al. Origin of giant dielectric response in nonferroelectric CaCu3Ti4O12: inhomogeneous conduction nature probed by atomic force microscopy [J]. Chemistry of Materials, 2008, 20(5): 1694–1698. doi: 10.1021/cm0710507 [42] CHUNG S Y, KIM I D, KANG S J L. Strong nonlinear current-voltage behaviour in perovskite-derivative calcium copper titanate [J]. Nature Materials, 2004, 3(11): 774–778. doi: 10.1038/nmat1238 [43] CLARKE D R. Varistor ceramics [J]. Journal of the American Ceramic Society, 1999, 82(3): 485–502. doi: 10.1111/j.1151-2916.1999.tb01793.x [44] FALCÓN H, ALONSO J A, SÁNCHEZ-BENÍTEZ J, et al. Crystal structure, magnetic and electrical properties of CaCu3Mn4− x Ti x O12 (0.3≤ x≤ 3.0) perovskites [J]. Journal of Physics: Condensed Matter, 2006, 18(29): 6841–6852. doi: 10.1088/0953-8984/18/29/021 [45] DENG G C, XANTHOPOULOS N, MURALT P. Chemical nature of colossal dielectric constant of CaCu3Ti4O12 thin film by pulsed laser deposition [J]. Applied Physics Letters, 2008, 92(17): 172909. doi: 10.1063/1.2919076 [46] JACOB K T, SHEKHAR C, LI X G, et al. Gibbs energy of formation of CaCu3Ti4O12 and phase relations in the system CaO-CuO/Cu2O-TiO2 [J]. Acta Materialia, 2008, 56(17): 4798–4803. doi: 10.1016/j.actamat.2008.05.038 [47] AMARAL F, RUBINGER C P L, VALENTE M A, et al. Enhanced dielectric response of GeO2-doped CaCu3Ti4O12 ceramics [J]. Journal of Applied Physics, 2009, 105(3): 034109. doi: 10.1063/1.3075909 [48] CHOI S Y, CHUNG S Y, YAMAMOTO T, et al. Direct determination of dopant site selectivity in ordered perovskite CaCu3Ti4O12 polycrystals by aberration-corrected STEM [J]. Advanced Materials, 2009, 21(8): 885–889. doi: 10.1002/adma.200802728 [49] DENG G C, MURALT P. Annealing effects on electrical properties and defects of CaCu3Ti4O12 thin films deposited by pulsed laser deposition [J]. Physical Review B, 2010, 81(22): 224111. doi: 10.1103/PhysRevB.81.224111 [50] YAMADA I, TAKATA K, HAYASHI N, et al. A perovskite containing quadrivalent iron as a charge-disproportionated ferrimagnet [J]. Angewandte Chemie International Edition, 2008, 47(37): 7032–7035. doi: 10.1002/anie.200801482 [51] XIANG H P, LIU X J, ZHAO E J, et al. Ferrimagnetic and half-metallic CaCu3Fe4O12: prediction from first principles investigation [J]. Applied Physics Letters, 2007, 91(1): 011903. doi: 10.1063/1.2753734 [52] MIZUMAKI M, CHEN W T, SAITO T, et al. Direct observation of the ferrimagnetic coupling of A-site Cu and B-site Fe spins in charge-disproportionated CaCu3Fe4O12 [J]. Physical Review B, 2011, 84(9): 094418. doi: 10.1103/PhysRevB.84.094418 [53] LONG Y W. A-site ordered quadruple perovskite oxides AAʹ3B4O12 [J]. Chinese Physics B, 2016, 25(7): 078108. doi: 10.1088/1674-1056/25/7/078108 [54] YAMADA I, TSUCHIDA K, OHGUSHI K, et al. Giant negative thermal expansion in the iron perovskite SrCu3Fe4O12 [J]. Angewandte Chemie International Edition, 2011, 50(29): 6579–6582. doi: 10.1002/anie.201102228 [55] TAKENAKA K, TAKAGI H. Giant negative thermal expansion in Ge-doped anti-perovskite manganese nitrides [J]. Applied Physics Letters, 2005, 87(26): 261902. doi: 10.1063/1.2147726 [56] HAO X F, XU Y H, GAO F M, et al. Charge disproportionation in CaCu3Fe4O12 [J]. Physical Review B, 2009, 79(11): 113101. doi: 10.1103/PhysRevB.79.113101 [57] LI H P, LV S H, WANG Z C, et al. Mechanism of A-B intersite charge transfer and negative thermal expansion in A-site-ordered perovskite LaCu3Fe4O12 [J]. Journal of Applied Physics, 2012, 111(10): 103718. doi: 10.1063/1.4721408 [58] CHEN W T, SAITO T, HAYASHI N, et al. Ligand-hole localization in oxides with unusual valence Fe [J]. Scientific Reports, 2012, 2: 449. doi: 10.1038/srep00449 [59] ALLUB R, ALASCIO B. A thermodynamic model for the simultaneous charge/spin order transition in LaCu3Fe4O12 [J]. Journal of Physics: Condensed Matter, 2012, 24(49): 495601. doi: 10.1088/0953-8984/24/49/495601 [60] ETANI H, YAMADA I, OHGUSHI K, et al. Suppression of intersite charge transfer in charge-disproportionated perovskite YCu3Fe4O12 [J]. Journal of the American Chemical Society, 2012, 135(16): 6100–6106. [61] YAMADA I, ETANI H, TSUCHIDA K, et al. Control of bond-strain-induced electronic phase transitions in iron perovskites [J]. Inorganic Chemistry, 2013, 52(23): 13751–13761. doi: 10.1021/ic402344m [62] REZAEI N, HANSMANN P, BAHRAMY M S, et al. Mechanism of charge transfer/disproportionation in LnCu3Fe4O12 (Ln=lanthanides) [J]. Physical Review B, 2014, 89(12): 125125. doi: 10.1103/PhysRevB.89.125125 [63] MENG J L, ZHANG L F, YAO F, et al. Theoretical study on the negative thermal expansion perovskite LaCu3Fe4O12: pressure-triggered transition of magnetism, charge, and spin state [J]. Inorganic Chemistry, 2017, 56(11): 6371–6379. doi: 10.1021/acs.inorgchem.7b00458 [64] YAMADA I, MARUKAWA S, MURAKAMI M, et al. “True” negative thermal expansion in Mn-doped LaCu3Fe4O12 perovskite oxides [J]. Applied Physics Letters, 2014, 105(23): 231906. doi: 10.1063/1.4903890 [65] SAKAI Y, YANG J Y, YU R Z, et al. A-site and B-site charge orderings in an s- d level controlled perovskite oxide PbCoO3 [J]. Journal of the American Chemical Society, 2017, 139(12): 4574–4581. doi: 10.1021/jacs.7b01851 [66] LIU Z H, SAKAI Y, YANG J Y, et al. Sequential spin state transition and intermetallic charge transfer in PbCoO3 [J]. Journal of the American Chemical Society, 2020, 142(12): 5731–5741. doi: 10.1021/jacs.9b13508 [67] OVSYANNIKOV S V, ABAKUMOV A M, TSIRLIN A A, et al. Perovskite-like Mn2O3: a path to new manganites [J]. Angewandte Chemie International Edition, 2013, 52(5): 1494–1498. doi: 10.1002/anie.201208553 [68] BYKOVA E, DUBROVINSKY L, DUBROVINSKAIA N, et al. Structural complexity of simple Fe2O3 at high pressures and temperatures [J]. Nature Communications, 2016, 7: 10661. doi: 10.1038/ncomms10661 [69] SMOLENSKII G A, BOKOV V A. Coexistence of magnetic and electric ordering in crystals [J]. Journal of Applied Physics, 1964, 35(3): 915–918. doi: 10.1063/1.1713535 [70] KIMURA T, GOTO T, SHINTANI H, et al. Magnetic control of ferroelectric polarization [J]. Nature, 2003, 426(6962): 55–58. doi: 10.1038/nature02018 [71] WANG J, NEATON J B, ZHENG H, et al. Epitaxial BiFeO3 multiferroic thin film heterostructures [J]. Science, 2003, 299(5613): 1719–1722. doi: 10.1126/science.1080615 [72] KHOMSKII D I. Multiferroics: different ways to combine magnetism and ferroelectricity [J]. Journal of Magnetism and Magnetic Materials, 2006, 306(1): 1–8. doi: 10.1016/j.jmmm.2006.01.238 [73] DONG S, LIU J M, CHEONG S W, et al. Multiferroic materials and magnetoelectric physics: symmetry, entanglement, excitation, and topology [J]. Advances in Physics, 2015, 64(5/6): 519–626. [74] POPOV Y F, KADOMTSEVA A M, KROTOV S S, et al. Features of the magnetoelectric properties of BiFeO3 in high magnetic fields [J]. Low Temperature Physics, 2001, 27(6): 478–479. doi: 10.1063/1.1382990 [75] TOKURA Y, SEKI S, NAGAOSA N. Multiferroics of spin origin [J]. Reports on Progress in Physics, 2014, 77(7): 076501. doi: 10.1088/0034-4885/77/7/076501 [76] GAJEK M, BIBES M, FUSIL S, et al. Tunnel junctions with multiferroic barriers [J]. Nature Materials, 2007, 6(4): 296–302. doi: 10.1038/nmat1860 [77] CHU Y H, MARTIN L W, HOLCOMB M B, et al. Electric-field control of local ferromagnetism using a magnetoelectric multiferroic [J]. Nature Materials, 2008, 7(6): 478–482. doi: 10.1038/nmat2184 [78] SHEVLIN S. Multiferroics and the path to the market [J]. Nature Materials, 2019, 18(3): 191–192. doi: 10.1038/s41563-019-0295-6 [79] NAN T X, LIN H, GAO Y, et al. Acoustically actuated ultra-compact NEMS magnetoelectric antennas [J]. Nature Communications, 2017, 8(1): 296. doi: 10.1038/s41467-017-00343-8 [80] LONG Y W, SAITO T, MIZUMAKI M, et al. Various valence states of square-coordinated Mn in A-site-ordered perovskites [J]. Journal of the American Chemical Society, 2009, 131(44): 16244–16247. doi: 10.1021/ja906668c [81] LV S H, LI H P, LIU X J, et al. Mn-Cr intersite independent magnetic behavior and electronic structures of LaMn3Cr4O12: study from first-principles [J]. Journal of Applied Physics, 2011, 110(2): 023711. doi: 10.1063/1.3610504 [82] 殷云宇, 王潇, 邓宏芟, 等. 多种有序钙钛矿结构的高压制备与特殊物性 [J]. 物理学报, 2017, 66(3): 030201. doi: 10.7498/aps.66.030201YIN Y Y, WANG X, DENG H S, et al. High-pressure synthesis and special physical properties of several ordered perovskite structures [J]. Acta Physica Sinica, 2017, 66(3): 030201. doi: 10.7498/aps.66.030201 [83] SCHIRBER M. Multiferroic surprise [J]. Physics, 2015, 8: s95. doi: 10.1103/Physics.8.s95 [84] FENG J S, XIANG H J. Anisotropic symmetric exchange as a new mechanism for multiferroicity [J]. Physical Review B, 2016, 93(17): 174416. doi: 10.1103/PhysRevB.93.174416 [85] HUR N, PARK S, SHARMA P A, et al. Electric polarization reversal and memory in a multiferroic material induced by magnetic fields [J]. Nature, 2004, 429(6990): 392–395. doi: 10.1038/nature02572 [86] ZHOU L, DAI J H, CHAI Y S, et al. Realization of large electric polarization and strong magnetoelectric coupling in BiMn3Cr4O12 [J]. Advanced Materials, 2017, 29(44): 1703435. doi: 10.1002/adma.201703435 [87] 周龙, 王潇, 张慧敏, 等. 多阶有序钙钛矿多铁性材料的高压制备与物性 [J]. 物理学报, 2018, 67(15): 157505. doi: 10.7498/aps.67.20180878ZHOU L, WANG X, ZHANG H M, et al. High pressure synthesis and physical properties of multiferroic materials with multiply-ordered perovskite structure [J]. Acta Physica Sinica, 2018, 67(15): 157505. doi: 10.7498/aps.67.20180878 [88] LIU G X, LIU Z H, CHAI Y S, et al. Magnetic and electric field dependent anisotropic magnetoelectric multiferroicity in SmMn3Cr4O12 [J]. Physical Review B, 2021, 104(5): 054407. [89] TANDA S, TSUNETA T, OKAJIMA Y, et al. A Möbius strip of single crystals [J]. Nature, 2002, 417(6887): 397–398. doi: 10.1038/417397a [90] HAN D R, PAL S, LIU Y, et al. Folding and cutting DNA into reconfigurable topological nanostructures [J]. Nature Nanotechnology, 2010, 5(10): 712–717. doi: 10.1038/nnano.2010.193 [91] GRAY A. Modern differential geometry of curves and surfaces with mathematica [M]. 2nd ed. Boca Raton: CRC Press, 1997. [92] LIU G X, PI M C, ZHOU L, et al. Physical realization of topological Roman surface by spin-induced ferroelectric polarization in cubic lattice [J]. Nature Communications, 2022, 13(1): 2373. doi: 10.1038/s41467-022-29764-w [93] WANG Z W, CHAI Y S, DONG S. First-principles demonstration of Roman-surface topological multiferroicity [J]. Physical Review B, 2023, 108(6): L060407. doi: 10.1103/PhysRevB.108.L060407 [94] BAIBICH M N, BROTO J M, FERT A, et al. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices [J]. Physical Review Letters, 1988, 61(21): 2472–2475. doi: 10.1103/PhysRevLett.61.2472 [95] MOTT N F. The electrical conductivity of transition metals [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1936, 153(880): 699-717. [96] PICKETT W E, MOODERA J S. Half metallic magnets [J]. Physics Today, 2001, 54(5): 39–44. doi: 10.1063/1.1381101 [97] PARK J H, VESCOVO E, KIM H J, et al. Direct evidence for a half-metallic ferromagnet [J]. Nature, 1998, 392(6678): 794–796. doi: 10.1038/33883 [98] HWANG H Y, CHEONG S W, ONG N P, et al. Spin-polarized intergrain tunneling in La2/3Sr1/3MnO3 [J]. Physical Review Letters, 1996, 77(10): 2041–2044. doi: 10.1103/PhysRevLett.77.2041 [99] KOBAYASHI K I, KIMURA T, SAWADA H, et al. Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure [J]. Nature, 1998, 395(6703): 677–680. doi: 10.1038/27167 [100] KOBAYASHI K I, KIMURA T, TOMIOKA Y, et al. Intergrain tunneling magnetoresistance in polycrystals of the ordered double perovskite Sr2FeReO6 [J]. Physical Review B, 1999, 59(17): 11159–11162. doi: 10.1103/PhysRevB.59.11159 [101] LIU Z H, ZHANG S K, WANG X, et al. Realization of a half metal with a record-high Curie temperature in perovskite oxides [J]. Advanced Materials, 2022, 34(17): 2200626. doi: 10.1002/adma.202200626 [102] WANG X, LIU Z H, DENG H S, et al. Comparative study on the magnetic and transport properties of B-site ordered and disordered CaCu3Fe2Os2O12 [J]. Inorganic Chemistry, 2022, 61(42): 16929–16935. doi: 10.1021/acs.inorgchem.2c03030 [103] EL GANICH H, EL RHAZOUANI O, AHMED Y A, et al. Computation of the exchange interactions in CaCu3Fe2Os2O12 quadruple perovskite: Monte Carlo simulation [J]. Physica E: Low-Dimensional Systems and Nanostructures, 2023, 150: 115696. doi: 10.1016/j.physe.2023.115696 [104] MEHMOOD S, ALI Z, ALHARBI Y T, et al. Structural and magneto-elastic properties of the quadruple perovskites CaCu3B2Os2O12 (B=Mn–Ni): the Heisenberg model and DFT study [J]. Journal of Electronic Materials, 2023, 52(9): 5872–5883. doi: 10.1007/s11664-023-10555-y [105] LIU Z H, SUN Q, YE X B, et al. Quadruple perovskite oxide LaCu3Co2Re2O12: a ferrimagnetic half metal with nearly 100% B-site degree of order [J]. Applied Physics Letters, 2020, 117(15): 152402. doi: 10.1063/5.0025704 [106] WANG X, LIU M, SHEN X D, et al. High-temperature ferrimagnetic half metallicity with wide spin-up energy gap in NaCu3Fe2Os2O12 [J]. Inorganic Chemistry, 2019, 58(1): 320–326. doi: 10.1021/acs.inorgchem.8b02404 [107] WANG X, LIU Z H, YE X B, et al. Os doping suppressed Cu-Fe charge transfer and induced structural and magnetic phase transitions in LaCu3Fe4− x Os x O12 ( x = 1 and 2) [J]. Inorganic Chemistry, 2021, 60(9): 6298–6305. doi: 10.1021/acs.inorgchem.1c00009 [108] YE X B, WANG X, LIU Z H, et al. Emergent physical properties of perovskite-type oxides prepared under high pressure [J]. Dalton Transactions, 2022, 51(5): 1745–1753. doi: 10.1039/D1DT03551G [109] LI X X, WU X J, LI Z Y, et al. Bipolar magnetic semiconductors: a new class of spintronics materials [J]. Nanoscale, 2012, 4(18): 5680–5685. doi: 10.1039/c2nr31743e [110] KATSNELSON M I, IRKHIN V Y, CHIONCEL L, et al. Half-metallic ferromagnets: from band structure to many-body effects [J]. Reviews of Modern Physics, 2008, 80(2): 315–378. doi: 10.1103/RevModPhys.80.315 [111] YAMADA I, FUJII H, TAKAMATSU A, et al. Bifunctional oxygen reaction catalysis of quadruple manganese perovskites [J]. Advanced Materials, 2017, 29(4): 1603004. doi: 10.1002/adma.201603004 [112] YE X B, SONG S Z, LI L L, et al. Aʹ-B intersite cooperation-enhanced water splitting in quadruple perovskite oxide CaCu3Ir4O12 [J]. Chemistry of Materials, 2021, 33(23): 9295–9305. doi: 10.1021/acs.chemmater.1c03015 [113] AKIZUKI Y, YAMADA I, FUJITA K, et al. A-site-ordered perovskite MnCu3V4O12 with a 12-coordinated manganese (Ⅱ) [J]. Inorganic Chemistry, 2013, 52(19): 11538–11543. doi: 10.1021/ic401855j [114] AKIZUKI Y, YAMADA I, FUJITA K, et al. Rattling in the quadruple perovskite CuCu3V4O12 [J]. Angewandte Chemie International Edition, 2015, 54(37): 10870–10874. doi: 10.1002/anie.201504784 [115] CONG J Z, ZHAI K, CHAI Y S, et al. Spin-induced multiferroicity in the binary perovskite manganite Mn2O3 [J]. Nature Communications, 2018, 9(1): 2996. doi: 10.1038/s41467-018-05296-0 [116] BARTEL C J, SUTTON C, GOLDSMITH B R, et al. New tolerance factor to predict the stability of perovskite oxides and halides [J]. Science Advances, 2019, 5(2): eaav0693. doi: 10.1126/sciadv.aav0693 [117] ALBRECHT E K, KARTTUNEN A J. Investigation on the predictive power of tolerance factor τ for A-site double perovskite oxides [J]. Dalton Transactions, 2023, 52(35): 12461–12469. doi: 10.1039/D3DT01990J [118] STRELTSOV S V, KHOMSKII D I. Jahn-Teller distortion and charge, orbital, and magnetic order in NaMn7O12 [J]. Physical Review B, 2014, 89(20): 201115(R). [119] JOHNSON R D, KHALYAVIN D D, MANUEL P, et al. Magneto-orbital ordering in the divalent A-site quadruple perovskite manganites AMn7O12 (A=Sr, Cd, and Pb) [J]. Physical Review B, 2017, 96(5): 054448. doi: 10.1103/PhysRevB.96.054448 [120] BELIK A A, JOHNSON R D, KHALYAVIN D D. The rich physics of A-site-ordered quadruple perovskite manganites AMn7O12 [J]. Dalton Transactions, 2021, 50(43): 15458–15472. doi: 10.1039/D1DT02992D -



















 下载:
下载:









































 下载:
下载: