破片式战斗部空中爆炸下冲击波与破片的耦合作用

陈长海; 侯海量; 朱锡; 胡年明; 李典

doi:10.11858/gywlxb.20170849

破片式战斗部空中爆炸下冲击波与破片的耦合作用

doi: 10.11858/gywlxb.20170849

海军工程大学舰船工程系，湖北武汉 430033

基金项目:

国家自然科学基金 51409253

国家自然科学基金 51479204

详细信息

作者简介:
陈长海(1985—), 男, 博士, 讲师, 主要从事舰船结构毁伤力学研究. E-mail:chenchanghai0746@163.com

中图分类号: O382.1
计量
- 文章访问数: 7076
- HTML全文浏览量: 3075
- PDF下载量: 427
出版历程
- 收稿日期: 2017-09-16
- 修回日期: 2017-11-06

Coupling Action Spans for Air-Blast Waves and Fragments by Fragmentation Warheads Exploding in Air

Department of Naval Architecture Engineering, Naval University ofEngineering, Wuhan 430033, China

摘要

摘要: 为探讨破片式战斗部空中爆炸下冲击波与破片的耦合作用机制，通过分析冲击波和破片在空气中的运动规律，在考虑壳体对冲击波强度的影响下，建立了冲击波与破片耦合作用区间的理论计算模型，并采用相关文献试验结果进行了对比。在此基础上，结合实例讨论了耦合作用区间随各影响因素的变化规律。结果表明，战斗部装填系数、装药爆速、壳体厚度以及能量分配对耦合作用区间的影响较大，而装药爆热、破片质量及破片形状对耦合作用区间的影响较小；随着装填系数、装药爆热和爆速、破片质量及冲击波能量与破片动能的比值的增大，耦合作用区间均减小；而随着壳体厚度和破片形状不规则度的提高，耦合作用区间增大。
- 破片式战斗部 /
- 空爆冲击波 /
- 高速破片 /
- 耦合作用区间
Abstract: In the present work, to find out the mechanisms of the coupling effect for blast waves and fragments by fragmentation warheads exploding in the air, we developed a theoretical model by analyzing the motion patterns of the blast waves and fragments moving in the air in consideration of the influence of the shell on the intensity of the shock wave.Meanwhile, we carried out an analysis of an actual case and examined the factors that influence the coupling action spans.The results show that the warhead loading coefficients, detonation velocities, shell thicknesses and energy allocations have a great influence on the coupling action spans, whereas the influence of the explosion heats, masses and shapes of the fragments is relatively limited.The coupling action spans decrease with the increase of the loading coefficients, explosion heats and detonation velocities of the explosives, fragment masses and the energy ratio of the shock wave energy to the fragment kinetic energy.However, as the shell thickness gets bigger and the fragment shapes become more abnormal, the coupling action spans become larger.
- fragmentation warhead /
- air-blast wave /
- high-velocity fragment /
- coupling action span

HTML全文

破片式战斗部空中爆炸下会同时产生冲击波和高速破片。战斗部近距空爆情形下，冲击波与高速破片会存在耦合作用，此时不能简单地将两种毁伤载荷分开考虑。对于战斗部空爆的毁伤问题，早期的研究思路主要是将其解耦成冲击波对结构的破坏^[1]和高速破片的穿甲破坏^[2]两个问题进行考虑。随着研究的不断深入，人们逐渐认识到战斗部近距空爆情形下，冲击波与破片存在耦合效应，该耦合效应的存在会使结构的破坏效果较单一冲击波或高速破片单独作用时严重得多^[3-6]。因此，战斗部空中爆炸下冲击波与高速破片的耦合作用问题成为近些年来防护领域研究的热点和难点，而如何找出冲击波与破片的耦合作用区间则是耦合作用研究的一个重要内容。

现代半穿甲反舰导弹战斗部主要通过侵入舰艇舷侧内部后的近距空爆，形成冲击波和大量的高速破片，耦合作用于舰艇结构，从而造成更严重的破坏。通过研究冲击波与破片的耦合作用区间可以较准确地得出冲击波与破片的耦合作用区间大小，从而尽量避免舰艇防护结构遭受耦合作用毁伤，最大限度地发挥防护结构的防护效能。因此，冲击波与破片耦合作用区间的研究对于舰艇水上防护结构的设计具有重要意义。对于战斗部空中爆炸下冲击波与破片的先后作用问题，近些年来，研究者通过实验^[6-7]或数值仿真^{[5, 8-9]}进行了一些探讨，同时也开展了一定的理论分析^[10-11]。然而，对于战斗部空中爆炸下冲击波与破片耦合作用区间问题的研究，目前尚未见报道。

本研究通过推导冲击波和破片在空气中的运动规律，在考虑壳体对冲击波强度的影响下，建立破片式战斗部空中爆炸下冲击波与破片耦合作用区间的理论计算模型，并进行实例分析。在此基础上，讨论战斗部装填系数和装药类型等因素对冲击波与破片耦合作用区间大小的影响规律，明确耦合作用区间的主要影响因素以及耦合作用区间随各因素的变化规律。

1. 空爆冲击波的传播规律分析

战斗部装药在空气中爆炸时，将形成空爆冲击波。空爆冲击波在空气中传播时压力不断衰减，峰值超压Δp_m随传播距离的变化关系满足^[12]

$\Delta {p_{\rm{m}}}\left( {\bar r} \right) = \left\{ \begin{array}{l} \frac{{0.00625}}{{{{\bar r}^4}}} - \frac{{0.0357}}{{{{\bar r}^3}}} + \frac{{0.5540}}{{{{\bar r}^2}}} + \frac{{1.4072}}{{\bar r}}\;\;\;\;\;\;\;0.05 \le \bar r \le 0.50\\ \frac{{0.431}}{{{{\bar r}^3}}} + \frac{{0.301}}{{{{\bar r}^2}}} + \frac{{0.067}}{{\bar r}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.50 < \bar r \le 70.9 \end{array} \right.$

(1)

式中： $\bar r = R/\sqrt[3]{\omega }$ 为比例爆距，其中R为离爆炸中心的距离(m)，ω为战斗部等效TNT装药量(kg)。

距离爆心R处，空爆冲击波的正压作用时间t₊为^[12]

${t_ + } = 1.35 \times {10^{ - 3}}\sqrt[6]{\omega }\sqrt R$

(2)

冲击波在空气中的传播速度与其超压有关。根据冲击波的基本关系可得，空爆冲击波波阵面的传播速度v_s(m/s)与峰值超压Δp_m(MPa)之间的近似关系式为^[12]

${v_{\rm{s}}} = 340\sqrt {1 + 8.3\Delta {p_{\rm{m}}}\left( {\bar r} \right)}$

(3)

虽然通过积分或对时间进行迭代的计算方法可以获得空爆冲击波波阵面传播距离与时间的关系，但该方法计算过程较为复杂。因此，本研究首先采用幂函数拟合得到空爆冲击波波阵面传播速度与比例爆距的关系，然后通过积分转换得到传播距离与时间的关系式。

采用幂函数拟合所得空爆冲击波波阵面传播速度v_s与比例爆距 $\bar r$ 的关系(如图 1所示)

图 1 空爆冲击波波阵面传播速度与比例爆距的关系

Figure 1. Relation between scaled stand-off distance and propagation velocity of air-blast wave front

下载: 全尺寸图片幻灯片

${v_{\rm{s}}} = 1195.07{{\bar r}^{ - 0.76}}$

(4)

将比例爆距的表达式代入(4)式，即可得到空爆冲击波波阵面传播速度v_s与传播距离R_s的关系

${v_{\rm{s}}} = 1195.07{\omega ^{0.25}}R_{\rm{s}}^{ - 0.76}$

(5)

然后，对(5)式进行积分，整理得到空爆冲击波波阵面的传播距离R_s与时间t_s的关系

${R_{\rm{s}}} = {\left( {2103.32{\omega ^{0.25}}{t_{\rm{s}}}} \right)^{1/1.76}}$

(6)

2. 破片在空气中的运动规律分析

对于一般的柱形战斗部，其爆炸产生的破片初速v_f0可近似由格尼公式计算得到^[13]

${v_{{\rm{f0}}}} = \sqrt {2E} {\left( {\frac{\beta }{{1 + 0.5\beta }}} \right)^{1/2}}$

(7)

式中： $\sqrt {2E}$ 为格尼常数，β为战斗部的装填系数。

破片在空气中飞行时水平方向主要受到空气阻力的影响。假设破片的水平飞行弹道为直线，忽略空气升力和自身重力的影响，只考虑空气阻力作用，则其运动方程为

${m_{\rm{f}}}\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - \frac{1}{2}{c_{\rm{f}}}{\rho _0}\bar A{v^2}$

(8)

式中：v为破片的瞬时速度，m_f为战斗部破片设计质量，c_f为破片飞行的空气阻力系数，A为破片的平均迎风面积。对(8)式积分得到破片飞行速度v_f与飞行时间t_f的关系式

${v_{\rm{f}}} = \frac{{{v_{{\rm{f0}}}}}}{{1 + {c_{\rm{f}}}{\rho _0}\bar A{v_{{\rm{f0}}}}{t_{\rm{f}}}/\left( {2{m_{\rm{f}}}} \right)}}$

(9)

进一步积分得到破片飞行距离R_f与飞行时间t_f的关系式

${R_{\rm{f}}} = \frac{{2{m_{\rm{f}}}}}{{{c_{\rm{f}}}{\rho _0}\bar A}}\ln \left( {1 + \frac{{{c_{\rm{f}}}{\rho _0}\bar A{v_{{\rm{f0}}}}}}{{2{m_{\rm{f}}}}}{t_{\rm{f}}}} \right)$

(10)

在空气中飞行时，破片的平均迎风面积与其质量存在如下近似关系^[13]

$\bar A = \alpha m_{\rm{f}}^{2/3}$

(11)

式中：α为破片的形状系数。将(11)式代入(10)式整理后得到

${R_{\rm{f}}} = \frac{{2m_{\rm{f}}^{1/3}}}{{\alpha {c_{\rm{f}}}{\rho _0}}}\ln \left( {1 + \frac{{\alpha {c_{\rm{f}}}{\rho _0}{v_{{\rm{f0}}}}}}{{2m_{\rm{f}}^{1/3}}}{t_{\rm{f}}}} \right)$

(12)

通过转换可得破片飞行时间t_f与飞行距离R_f的关系式

${t_{\rm{f}}} = \frac{{2m_{\rm{f}}^{1/3}}}{{\alpha {c_{\rm{f}}}{\rho _0}{v_{{\rm{f0}}}}}}\left[ {\exp \left( {\frac{{\alpha {c_{\rm{f}}}{\rho _0}}}{{2m_{\rm{f}}^{1/3}}}{R_{\rm{f}}}} \right) - 1} \right]$

(13)

3. 壳体对冲击波强度的影响分析

战斗部爆炸形成冲击波和高速破片的过程中，装药的总内能主要转化为初始冲击波能E₀、爆轰气体的动能E₁和势能E₂以及破片总动能E_fk。由于壳体变形及破裂耗能占比很小且可忽略，因而有

${m_{\rm{e}}}{Q_v} = {E_0} + {E_1} + {E_2} + {E_{{\rm{fk}}}}$

(14)

式中：m_e和Q_v分别为战斗部装药质量和爆热。

破片形成及随后的加速过程中，爆轰气体的动能和势能最终都将转化为冲击波的能量^[14-15]，即空气冲击波的总能量E_st=E₀+E₁+E₂，根据(14)式可以得到

${E_{{\rm{st}}}} = {E_0} + {E_1} + {E_2} = {m_{\rm{e}}}{Q_v} - {E_{{\rm{fk}}}}$

(15)

将破片总动能E_fk=m_ftv_f0²/2代入(15)式整理得到

${E_{{\rm{st}}}} = {m_{\rm{e}}}{Q_v} - \frac{1}{2}{m_{{\rm{ft}}}}v_{{\rm{f0}}}^2 = {m_{\rm{e}}}{Q_v}\left( {1 - \frac{{{m_{{\rm{ft}}}}v_{{\rm{f0}}}^2}}{{2{m_{\rm{e}}}{Q_v}}}} \right)$

(16)

式中：m_ft为破片的总质量。令η=1-m_ftv_f0²/(2m_eQ_v)，则战斗部形成空气冲击波的装药即等效裸装药量为ηω。因此，考虑壳体对战斗部爆炸形成空气冲击波的影响，(5)式和(6)式修正为

${v_{\rm{s}}} = 1195.07{\left( {\eta \omega } \right)^{0.25}}R_{\rm{s}}^{ - 0.76}$

(17)

${R_{\rm{s}}} = {\left[ {2103.32{{\left( {\eta \omega } \right)}^{0.25}}{t_{\rm{s}}}} \right]^{1/1.76}}$

(18)

4. 战斗部极限膨胀半径计算

破片式战斗部爆炸形成高速破片的过程是爆轰气体对壳体膨胀做功并使破片加速的过程。战斗部爆炸过程中，壳体膨胀破裂形成破片。随后，破片被加速直至爆轰气体膨胀速度小于破片速度。此时，壳体膨胀半径称为战斗部的极限膨胀半径。忽略绕流效应，爆轰气体对破片的做功W_f为

${W_{\rm{f}}} = \int_{{r_0}}^{{R_0}} {{p_{\rm{i}}}{A_{\rm{f}}}{\rm{d}}r}$

(19)

式中：R₀为破片加速过程结束时壳体膨胀半径即战斗部的极限膨胀半径，r₀为战斗部壳体的初始半径，A_f为破片的面积，p_i为爆轰气体的瞬时压力。由爆轰气体的状态方程可得^[12]

${p_{\rm{i}}} = \left\{ \begin{array}{l} {p_0}{\left( {{r_0}/r} \right)^6}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p > 200{\rm{MPa}}\\ {p_0}{\left( {{r_0}/{r_{\rm{k}}}} \right)^6}{\left( {{r_{\rm{k}}}/r} \right)^{2.8}}\;\;\;\;\;\;p \le 200{\rm{MPa}} \end{array} \right.$

(20)

式中：p₀=ρ_eD_e²/8为初始压力，其中ρ_e和D_e分别为装药密度和爆速；r_k=r₀[p₀/(2×10⁸)]^1/6。

由于常规破片式战斗部爆炸时的p₀值远大于200 MPa，因而根据能量守恒原理，结合破片动能的表达式ρ_fA_fh_fv²/2并联立(19)式可得，破片加速过程结束时刻有(p>2×10⁸ Pa)

$\frac{1}{2}{\rho _{\rm{f}}}{h_{\rm{f}}}{v^2} = \frac{1}{5}{P_0}{r_0}\left[ {1 - {{\left( {\frac{{{r_0}}}{{{R_0}}}} \right)}^5}} \right]$

(21)

式中：v为破片瞬时速度，ρ_f和h_f分别为战斗部的材料密度和壳体厚度。

忽略绕流效应引起的能量损失，有

$v = \sqrt {7{p_0}/{\rho _{\rm{e}}}} {\left( {{r_0}/{R_0}} \right)^2}$

(22)

将(22)式代入(21)式整理得到

$R_0^5 - \frac{{35{\rho _{\rm{f}}}{h_{\rm{f}}}}}{{2{\rho _{\rm{e}}}}}r_0^3{R_0} - r_0^5 = 0$

(23)

求解(23)式可得战斗部的极限膨胀半径R₀，由于(23)式为超越方程，因此需要采用数值方法求解。

5. 耦合作用区间的计算

破片式战斗部空中爆炸下，初始冲击波速远大于破片初速，冲击波运动在破片之前。然而，由于冲击波的速度衰减很快，破片会追赶上冲击波。因此，存在破片与冲击波的追赶相遇问题。要得到冲击波与破片的耦合作用区间，需要先求出破片追赶上冲击波波阵面的距离及相应的时间。

将(18)式进行转化得到

${t_{\rm{s}}} = 4.75 \times {10^{ - 4}}{\left( {\eta \omega } \right)^{ - 0.25}}R_{\rm{s}}^{1.76}$

(24)

令R_s=R_f=R_m，且t_s=t_f=t_m，联立(24)式和(13)式可得

$4.75 \times {10^{ - 4}}{\left( {\eta \omega } \right)^{ - 0.25}}R_{\rm{m}}^{1.76} = \frac{{2m_{\rm{f}}^{1/3}}}{{{c_{\rm{f}}}{\rho _0}\alpha {v_{{\rm{f0}}}}}}\left[ {\exp \left( {\frac{{{c_{\rm{f}}}{\rho _0}\alpha }}{{2m_{\rm{f}}^{1/3}}}{R_{\rm{m}}}} \right) - 1} \right]$

(25)

求解(25)式即可得到破片追赶上冲击波波阵面的距离R_m。将R_m代入(24)式或(13)式，即可得到破片追赶上冲击波波阵面的时间t_m。由于(25)式为超越方程，需通过数值方法求解。

当破片追赶上冲击波波阵面后，破片运动在冲击波之前，破片先作用于结构。此时，冲击波与破片的耦合作用与结构自身振动周期T有关。由于破片穿甲舰艇防护结构的时间远小于结构自身的振动周期^[16]，因此可以近似认为，若在结构振动T/4时间内，冲击波能够到达，则该距离内破片作用后冲击波作用时仍会产生耦合作用效应。根据冲击波的传播规律可得，破片追赶上冲击波后的T/4时间内，冲击波波阵面传播的距离为

${R_{T/4}} = {R_{\rm{s}}}\left( {{t_{\rm{m}}} + T/4} \right) - {R_{\rm{s}}}\left( {{t_{\rm{m}}}} \right)$

(26)

耦合作用的最大距离R_cmax为

${R_{{\rm{cmax}}}} = {R_0} + {R_{\rm{m}}} + {R_{T/4}}$

(27)

综合上述讨论可知，破片式战斗部空中爆炸下，冲击波与破片的耦合作用区间为(R₀, R_cmax)。

6. 算例分析及讨论

采用文献[17]中某自然破片战斗部空中爆炸下的试验结果对上述理论计算模型进行验证。设破片战斗部TNT炸药当量为34.93 kg，其他相关参数设置如下：m_f=0.37 kg、ρ₀=1.25 kg/m³、c_f=0.3、A=19.72 cm²。试验得出，当破片初始速度为887 m/s时，冲击波与破片相遇的距离(R₀+R_m)约为10.2 m；另一方面，通过理论模型计算得到冲击波与破片相遇的距离约为9.84 m，与试验结果的相对误差为-3.5%，说明了理论计算模型的合理性和准确性。

进一步以某典型自然破片式导弹战斗部为例，对空爆冲击波和高速破片耦合作用区间的影响因素进行分析。设战斗部的总质量为230 kg，柱形装药直径为374.4 mm，装药质量为89.1 kg，装药密度为1.717 g/cm³；装药类型为B类混合装药，其格尼常数 $\sqrt {2E}$ =2 682 m/s，爆热Q_vB=4 969 J/g，TNT的爆热Q_vTNT=4 225 J/g；空气密度为1.23 kg/m³，壳体材料密度为7.8 g/cm³；破片设计质量取为战斗部平均破片设计质量(质量覆盖率0.95)，形状取为不规则矩形体(或菱形体)，破片阻力系数c_f=1.5，形状系数α=4.42×10^-3 m²/kg^2/3；舰艇防护结构的自身振动周期T=10 ms。

通过计算得到，该战斗部空中爆炸下冲击波与破片的耦合作用区间为(0.327 m, 7.376 m)。破片追赶上冲击波波阵面的时间为2.70 ms，相应的追赶距离为4.863 m。由(2)式可得，冲击波在4.863 m处的正压作用时间为7.00 ms，即破片追赶上冲击波的时间在其正压作用时间范围内，说明破片追赶上冲击波的距离计算结果是合理的。而在7.376 m处，冲击波的正压作用时间为8.6 ms，大于冲击波被破片超过后到达结构的时间T/4。由此可见，理论计算得到的耦合作用区间是合理的。

图 2为上面算例中冲击波传播距离和破片飞行距离随时间的变化情况。由图 2可知，当t < t_m时，冲击波波阵面运动在破片之前；当t=t_m时刻，两者相遇；而当t>t_m时，破片超过冲击波并运动在冲击波之前。在0 < t < t_m+T/4时间段内(对应的区间为R₀ < R < R_cmax)，冲击波与破片作用于结构时均存在耦合效应。换言之，若结构离战斗部爆心的距离处于(R₀, R_cmax)区间内，则结构会受到冲击波与破片的耦合作用毁伤。令R_cr=R₀+R_m，根据结构是否受到冲击波与破片的耦合作用，将整个距离空间分为4个区间。(1) r₀ < R≤R₀：战斗部壳体膨胀破裂即冲击波和破片的形成区间，两者向外运动的共同起点；(2) R₀ < R≤R_cr：冲击波运动在破片之前，冲击波先作用于结构，存在耦合作用效应；(3) R_cr < R≤R_cmax：破片运动在冲击波之前，破片先作用于结构，存在耦合作用效应；(4) R>R_cmax：破片始终运动在冲击波之前，可不考虑耦合作用效应，进行解耦处理。

图 2 传播距离随时间的变化

Figure 2. Propagation distances versus time

下载: 全尺寸图片幻灯片

通过算例分析可知，理论模型是合理的。(1)若不考虑壳体对冲击波强度的影响，则R_cmax计算值为7.870 m，与考虑壳体影响时的计算结果相差6.7%。由此可见，不考虑壳体对冲击波强度的影响下，耦合作用区间稍大。这主要是由于不考虑壳体影响情形下冲击波的压力更大，冲击波传播速度更快。由于冲击波后期的压力衰减很快，传播速度较慢，因而耦合作用区间增加不大。(2)破片大小和形状对其速度衰减有一定影响，因而对耦合作用区间大小也有一定的影响。由于质量大且形状规则的破片速度衰减相对较慢，耦合作用区间相对偏小，因此采用理论模型计算得到的耦合作用区间对于大质量破片而言是比较可靠的。(3)从壳体对冲击波强度的影响来看，壳体膨胀形成破片的确减小了形成冲击波的等效药量，降低了冲击波的压力和冲量。但是，从总冲量来看，冲击波的冲量和破片群的等效冲量之和大于不考虑壳体影响下的冲击波总冲量。

7. 耦合作用区间的影响因素分析

战斗部空中爆炸下冲击波与破片的耦合作用区间大小主要与冲击波的传播速度和破片运动速度有关，而决定这两个速度大小的直接因素则是战斗部的结构，包括装填系数、壳体性质(主要表现为爆炸形成破片质量的不同)、装药类型等。因此，通过对影响冲击波与破片耦合作用区间大小的因素进行分析，可以揭示各影响因素对耦合作用区间的影响规律，为战斗部设计提供参考。

7.1 装填系数的影响

保持战斗部壳体的总质量和直径不变，通过改变装药量得到装填系数β对耦合作用区间R_cmax的影响规律，如图 3所示。由图 3可知，随着战斗部装填系数的增大，空爆冲击波与破片的耦合作用区间不断减小，主要原因如下：装填系数增大时，破片初速提高，此时，破片能够在更短的距离内追赶上冲击波波阵面并更早地作用于结构，使得冲击波传播至结构表面及产生耦合作用的时长变短，导致耦合作用区间减小。虽然冲击波传播速度也随着装填系数的增大而增大，但是，由于破片速度的衰减速度远小于冲击波速度的衰减速度，因此破片初速成为决定耦合作用区间大小的主要内在因素。

图 3 装填系数对耦合作用区间大小的影响

Figure 3. Influence of loading coefficient on coupling action spans

下载: 全尺寸图片幻灯片

7.2 装药类型的影响

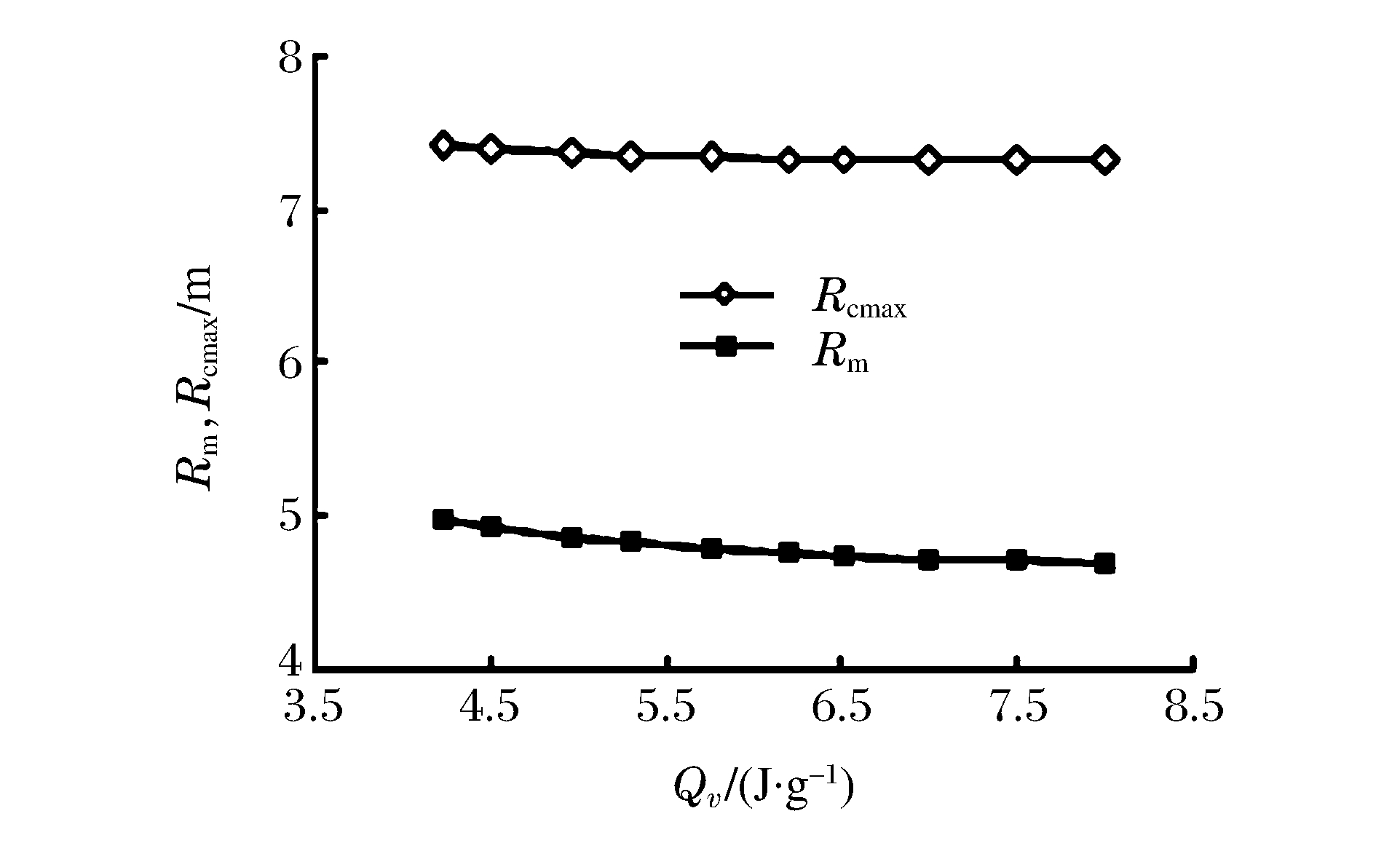
战斗部装药类型的差异主要体现在装药爆热及爆速上，以下分别对战斗部装药爆热和爆速对耦合作用区间的影响进行分析。首先令装药的爆速及其他参数不变，爆热不断增大，得到耦合作用区间R_cmax随爆热Q_v的变化如图 4所示。由图 4可知，耦合作用区间随着装药爆热的增大而减小，但是减小程度较小，即装药爆热对耦合作用区间的影响较小。主要原因如下：一方面，战斗部装药爆热的增大使其等效TNT当量增大，提高了装填系数，使破片的初速提高，能够更快追赶上冲击波波阵面(参考图 4中R_m随爆热的变化)；另一方面，装药爆热的增加也使冲击波的传播速度增大，冲击波被破片追赶上以后T/4时间内传播的距离增大，抵消了一部分由于R_m减小所引起的耦合作用区间减小的影响。

图 4 装药爆热对耦合作用区间大小的影响

Figure 4. Influence of detonation heat on coupling action spans

下载: 全尺寸图片幻灯片

由于装药爆速与格尼常数直接相关，因此装药爆速对耦合作用区间的影响不同于装药爆热。保持战斗部装药爆热和其他参数不变，改变装药爆速，得到耦合作用区间R_cmax随装药爆速D_e的变化规律如图 5所示。从图 5中可以看出，随着装药爆速的增加，耦合作用区间近似呈直线下降，说明装药爆速对耦合作用区间的影响很大。一方面，破片初速计算公式中格尼常数与装药爆速有关，且近似呈线性增长关系^[12]。装药爆速越高，格尼常数越大，破片初速越高，破片追赶上冲击波波阵面的距离就越短。另一方面，破片初速的提高会导致产生冲击波的等效裸装药减小，使冲击波的传播速度下降，被破片追赶上后T/4时间内传播的距离变短。这两方面的原因导致耦合作用区间随装药爆速的增加而急剧减小。进一步比较图 4和图 5可知，相对于装药爆热而言，装药爆速对耦合作用区间的影响更大。换言之，冲击波与破片耦合作用区间大小对装药爆速更敏感，受装药爆速的影响更加明显。主要原因在于，装药爆速能更直接、更有效地提高破片初速，而破片初速是决定耦合作用区间的主要内在因素，因而导致装药爆速比装药爆热对耦合作用区间的影响大得多。

图 5 装药爆速对耦合作用区间大小的影响

Figure 5. Influence of detonation velocity on coupling action spans

下载: 全尺寸图片幻灯片

7.3 破片质量的影响

战斗部爆炸会产生质量不同的高速破片，不同质量的高速破片在空气中的速度衰减快慢有所差异。在保持破片初速及形状相同的情况下，改变单枚破片质量得到冲击波与破片耦合作用区间的影响规律，如图 6所示。由图 6可以看出，耦合作用区间R_cmax随破片质量的增大而有所减小，但减小幅度很小。这说明破片质量对耦合作用区间大小有一定影响，但影响程度很小。主要原因在于：一方面，破片本身在空气中的速度衰减效应较弱，另一方面，破片追赶上冲击波波阵面的时间较短，因此大质量破片与小质量破片的速度衰减差别不大，尽管大质量破片的速度衰减慢于小质量破片。由于破片初速和形状相同，不同质量破片的速度衰减又差别不大，而破片初速是决定耦合作用区间的主要内在因素，因此破片质量对耦合作用区间的影响很小。

图 6 破片质量对耦合作用区间大小的影响

Figure 6. Influence of fragment mass on coupling action spans

下载: 全尺寸图片幻灯片

7.4 破片形状的影响

不同形状的破片在空气中的速度衰减也存在差异。保持破片的初速和质量相同，改变破片的形状，得到冲击波与破片耦合作用区间随破片形状的变化规律，如图 7所示，Spherical表示球形破片，Cubic表示立方体破片，Reg.R(Rh)表示规则矩形体(或菱形体)破片，Irreg.R(Rh)则表示不规则矩形体(或菱形体)破片。由图 7可知，球形破片、立方体破片、规则和不规则矩形体(或菱形体)破片的耦合作用区间依次增大。主要原因在于，球形、立方体、规则和不规则矩形体(或菱形体)破片的迎风阻力系数和形状系数均依次增大，导致速度衰减效应依次提高，使得追赶上冲击波波阵面的时间及相应距离依次增加，进而导致耦合作用区间R_cmax依次增大。但是，从图 7还可以看出，耦合作用区间随破片形状的变化量较小，导致该结果的原因主要有以下两个方面：(1)破片本身在空气中的速度衰减效应较弱，(2)破片追赶上冲击波波阵面的时间较短。

图 7 破片形状对耦合作用区间大小的影响

Figure 7. Influence of fragment shape on coupling action spans

下载: 全尺寸图片幻灯片

7.5 壳体厚度的影响

破片式战斗部壳体厚度的不同会导致爆炸形成的单个破片质量有所差异，同时还会对破片初速产生影响。以算例中的典型战斗部为分析对象，在保持装药类型和装药量不变的情况下，通过改变壳体厚度，得到壳体厚度对冲击波与破片耦合作用区间R_cmax的影响规律，如图 8所示。

图 8 壳体厚度对耦合作用区间大小的影响

Figure 8. Influence of shell thickness on coupling action spans

下载: 全尺寸图片幻灯片

由图 8可知，随着壳体厚度的增加，耦合作用区间近似呈线性增大，且增大的幅度较大，主要原因是：增加战斗部的壳体厚度相当于减小战斗部的装填系数，使得战斗部爆炸形成的破片初速大大降低。尽管壳体厚度的增加会增大破片的质量，使破片速度衰减变慢，但是由于破片在空气中衰减效应较弱，而破片初速则是决定耦合作用区间大小的主要内在因素，因此，随着壳体厚度的增大，破片初速降低，耦合作用区间明显变大。应该指出的是，在7.1节对装填系数的影响分析中，是通过增加战斗部装药量实现装填系数的增大，本节则是通过减小壳体厚度的方式达到装填系数增大的目的。从对耦合作用区间影响的规律来看，这两种方式的效果是一致的。另外还需要指出，虽然耦合作用区间随着壳体厚度的增大而增大，但是，当耦合作用区间增大到一定程度后，冲击波的强度较弱，此时，尽管冲击波与破片在理论上仍存在耦合作用，实际耦合作用却并不大。

7.6 能量分配的影响

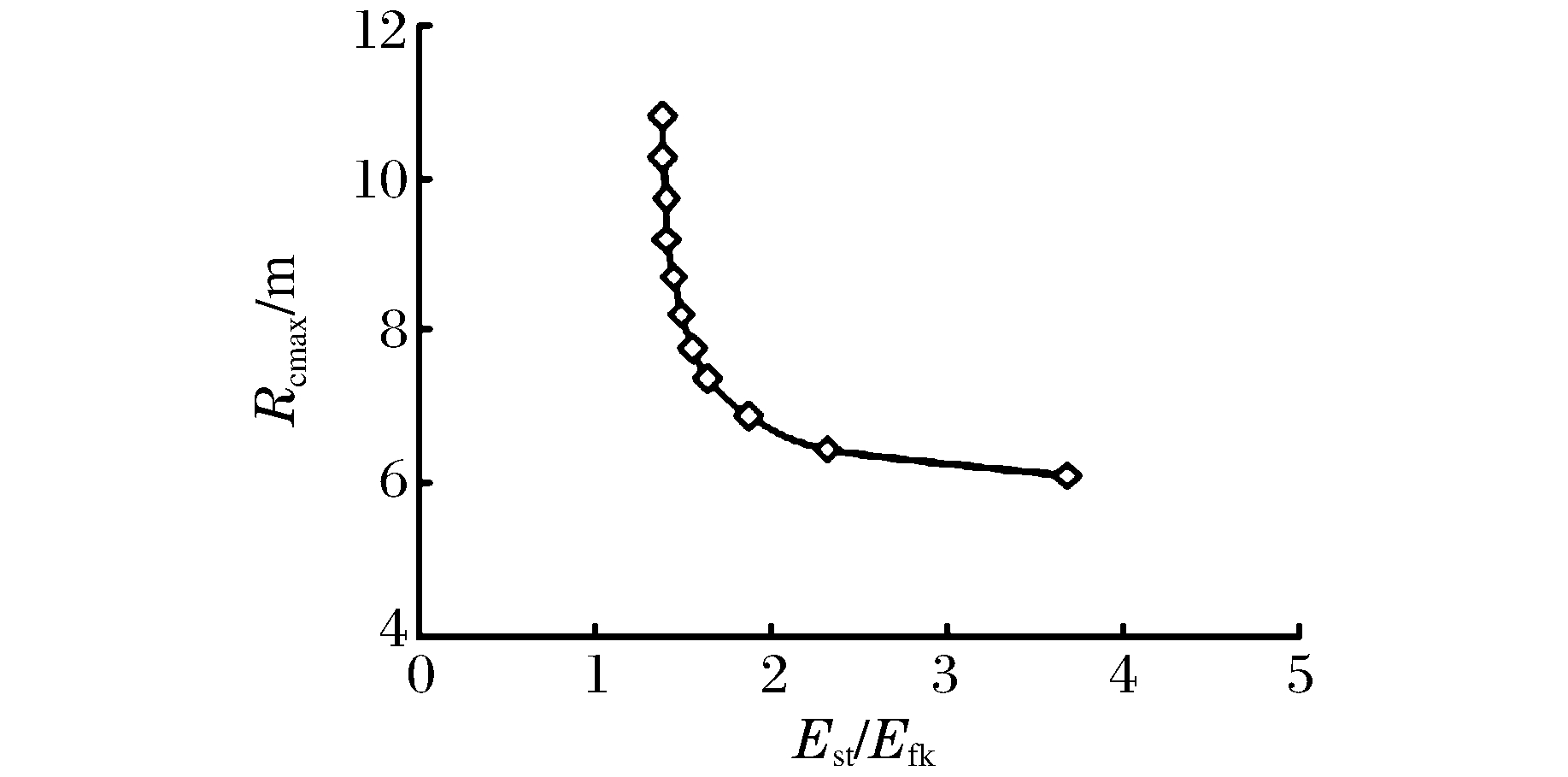
图 9给出了战斗部爆炸产生的冲击波能与破片动能的能量分配对耦合作用区间的影响规律，其中E_st为冲击波总能量，E_fk为破片总动能。从图 9中可以看出，随着冲击波能量与破片动能之比E_st/E_fk的增大，耦合作用区间R_cmax的值近似以幂指数规律急剧下降。主要原因在于，提高冲击波能量与破片动能的比值必然要增大装药量或减小壳体总质量，这两种方式都会增大战斗部装填系数，导致破片初速明显提高。结合7.2节中分析可知，破片初速是决定冲击波与破片耦合作用区间的主要内在因素，因此冲击波能量与破片动能比值的增大会增大破片初速，大大缩短破片追赶上冲击波波阵面所需要的时间及距离，从而明显地减小冲击波与破片耦合作用区间R_cmax。

图 9 能量分配对耦合作用区间大小的影响

Figure 9. Influence of energy distribution on coupling action spans

下载: 全尺寸图片幻灯片

8. 结论

(1) 通过与相关文献试验结果的对比，验证了所建立理论模型的合理性和有效性，因此工程上可以采用该理论模型估算破片式战斗部空中爆炸下冲击波与破片的耦合作用区间。

(2) 战斗部装填系数对耦合作用区间的影响较大，随着装填系数的增大，耦合作用区间相应减小。

(3) 装药爆热对耦合作用区间的影响较小，而装药爆速对耦合作用区间的影响较大；随着两者的增大，耦合作用区间均相应减小。

(4) 破片质量和形状对耦合作用区间的影响均较小，随着破片质量的增大，耦合作用区间相应减小；而随着破片形状不规则度的提高，耦合作用区间相应增大。

(5) 战斗部壳体厚度对耦合作用区间的影响较大，随着壳体厚度的增加，耦合作用区间相应增大。

(6) 战斗部空中爆炸下，形成冲击波的总能量与破片总动能的能量分配对耦合作用区间的影响较大，随着冲击波总能量与破片总动能的能量比的提高，耦合作用区间相应减小。

图 1 空爆冲击波波阵面传播速度与比例爆距的关系

Figure 1. Relation between scaled stand-off distance and propagation velocity of air-blast wave front

下载: 全尺寸图片幻灯片

图 2 传播距离随时间的变化

Figure 2. Propagation distances versus time

下载: 全尺寸图片幻灯片

图 3 装填系数对耦合作用区间大小的影响

Figure 3. Influence of loading coefficient on coupling action spans

下载: 全尺寸图片幻灯片

图 4 装药爆热对耦合作用区间大小的影响

Figure 4. Influence of detonation heat on coupling action spans

下载: 全尺寸图片幻灯片

图 5 装药爆速对耦合作用区间大小的影响

Figure 5. Influence of detonation velocity on coupling action spans

下载: 全尺寸图片幻灯片

图 6 破片质量对耦合作用区间大小的影响

Figure 6. Influence of fragment mass on coupling action spans

下载: 全尺寸图片幻灯片

图 7 破片形状对耦合作用区间大小的影响

Figure 7. Influence of fragment shape on coupling action spans

下载: 全尺寸图片幻灯片

图 8 壳体厚度对耦合作用区间大小的影响

Figure 8. Influence of shell thickness on coupling action spans

下载: 全尺寸图片幻灯片

图 9 能量分配对耦合作用区间大小的影响

Figure 9. Influence of energy distribution on coupling action spans

下载: 全尺寸图片幻灯片

参考文献(17)

[1]	蒋志刚, 白志海, 严波, 等.金属薄板与加筋板爆炸冲击响应研究进展[J].振动与冲击, 2010, 29(11):41-46. doi: 10.3969/j.issn.1000-3835.2010.11.010 JIANG Z G, BAI Z H, YAN B, et al.Advances in study on impact response of thin and stiffened metal plates under blast loading[J]. Journal of Vibration and Shock, 2010, 29(11):41-46. doi: 10.3969/j.issn.1000-3835.2010.11.010
[2]	王晓强, 朱锡.舰船用钢的抗弹道冲击性能研究进展[J].中国造船, 2010, 51(1):227-236. http://d.wanfangdata.com.cn/Periodical_zgzc201001029.aspx WANG X Q, ZHU X.Review on ballistic impact resistance of ship building steel[J]. Shipbuilding of China, 2010, 51(1):227-236. http://d.wanfangdata.com.cn/Periodical_zgzc201001029.aspx
[3]	何翔, 庞伟宾, 曲建波, 等.防护门在空气冲击波和破片作用下的破坏[J].爆炸与冲击, 2004, 24(5):475-479. http://d.old.wanfangdata.com.cn/Periodical/bzycj200405017 HE X, PANG W B, QU J B, et al.Protective door damaged by air shock wave and fragment arisen from explosion in prototype tunnel[J]. Explosion and Shock Waves, 2004, 24(5):475-479. http://d.old.wanfangdata.com.cn/Periodical/bzycj200405017
[4]	李伟, 朱锡, 梅志远, 等.战斗部舱内爆炸对舱室结构毁伤的实验研究[J].舰船科学技术, 2009, 31(3):34-37. http://d.wanfangdata.com.cn/Periodical_jckxjs200903008.aspx LI W, ZHU X, MEI Z Y, et al.Experimental studies on damage effect of missile warhead on cabin's structure under internal explosion[J]. Ship Science and Technology, 2009, 31(3):34-37. http://d.wanfangdata.com.cn/Periodical_jckxjs200903008.aspx
[5]	NYSTRÖM U, GYLLTOFT K.Numerical studies of the combined effects of blast and fragment loading[J]. International Journal of Impact Engineering, 2009, 36(8):995-1005. doi: 10.1016/j.ijimpeng.2009.02.008
[6]	张成亮, 朱锡, 侯海量, 等.爆炸冲击波与高速破片对夹层结构的联合毁伤效应试验研究[J].振动与冲击, 2014, 33(15):184-188. http://www.cnki.com.cn/Article/CJFDTotal-ZDCJ201415033.htm ZHANG C L, ZHU X, HOU H L, et al.Tests for combined damage effect of blast waves and high-velocity fragments on composite sandwich plates[J]. Journal of Vibration and Shock, 2014, 33(15):184-188. http://www.cnki.com.cn/Article/CJFDTotal-ZDCJ201415033.htm
[7]	梁为民, 张晓忠, 梁仕发, 等.结构内爆炸破片与冲击波运动规律试验研究[J].兵工学报, 2009, 30(增刊2):223-227. https://www.cnki.com.cn/qikan-BIGO2009S2047.html LIANG W M, ZHANG X Z, LIANG S F, et al.Experimental research on motion law of fragment and shock wave under the condition of internal explosion[J]. Acta Armamentarii, 2009, 30(Suppl 2):223-227. https://www.cnki.com.cn/qikan-BIGO2009S2047.html
[8]	刘刚. 破片和冲击波对直升机结构联合作用的数值模拟研究[D]. 南京: 南京理工大学, 2013.
[9]	张媛. 杀爆战斗部对武装直升机的毁伤研究[D]. 南京: 南京理工大学, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2276980
[10]	赵德辉, 许金余, 张燕.武器爆炸条件下冲击波与弹片共同作用数值模拟分析[J].西北工业大学学报, 2006, 24(3):334-337. http://d.wanfangdata.com.cn/Periodical_xbgydxxb200603014.aspx ZHAO D H, XU J Y, ZHANG Y.Velocities and displacements of shrapnel and shock wave during blast[J]. Journal of Northwestern Polytechnical University, 2006, 24(3):334-337. http://d.wanfangdata.com.cn/Periodical_xbgydxxb200603014.aspx
[11]	吕晓聪, 许金余, 白二雷, 等.弹片与爆炸冲击波耦合作用分析[J].解放军理工大学学报(自然科学版), 2007, 8(6):640-644. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_jfjlgdxxb200706015 LÜ X C, XU J Y, BAI E L, et al.Analysis of coupling between shrapnel and blast shock wave[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2007, 8(6):640-644. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_jfjlgdxxb200706015
[12]	张守中.爆炸基本原理[M].北京:国防工业出版社, 1988.
[13]	王儒策, 赵国志.弹丸终点效应[M].北京:北京理工大学出版社, 1993.
[14]	张奇, 苗常青, 白春华, 等.壳体对爆炸空气冲击波强度的影响[J].应用力学学报, 2003, 20(3):145-147. doi: 10.3969/j.issn.1000-4939.2003.03.033 ZHANG Q, MIAO C Q, BAI C H, et al.The influence of shell on blast shock wave intensity[J]. Chinese Journal of Applied Mechanics, 2003, 20(3):145-147. doi: 10.3969/j.issn.1000-4939.2003.03.033
[15]	ZHANG Q, MIAO C Q, LIN D C, et al.Relation of fragment with air shock wave intensity for explosion in a shell[J]. International Journal of Impact Engineering, 2003, 28(1):1129-1141. https://www.sciencedirect.com/science/article/pii/S0734743X03000046
[16]	陈志坚.舰艇振动学[M].北京:国防工业出版社, 2010.
[17]	KELLER J A. Environment from internal detonation of warheads[R]. Engineering Sciences Laboratory, Dener Research Institute, 1997.