1.   引言

轮轨关系是高速铁路工程领域最重要的研究课题之一，严重的轮轨失效会造成一系列灾难性后果以及巨大的经济损失。车轮扁疤是一种主要的轮轨失效形式，通常在踏面制动和车轮长期运转中由于轮轨之间的摩擦而引起。随着列车运行速度的提高，含扁疤缺陷的车轮循环冲击轨道，导致钢轨、轨枕、车轮、轴承等关键部件出现高周疲劳，加剧萌生裂纹和裂纹扩展，严重影响设备的使用寿命和列车运行的平稳性及安全性，给行车安全造成极大隐患^[1-3]。此外，车轮扁疤引起的车辆振动以及冲击和滚动噪声极大地影响乘客的舒适度^[1]。

近些年来，国内外研究学者对车轮扁疤引起的轮轨冲击问题开展了大量的研究。实验研究方面，最早可以追溯到20世纪50年代^[2]，美国铁路协会利用现场实验获得了车轮扁疤引起的轮轨垂向冲击力与速度的关系，结果表明：在速度为32 km/h左右时，轮轨垂向冲击力出现一个小的峰值；之后随着速度的增加轮轨垂向冲击力不断减小；速度大于64 km/h时，轮轨垂向冲击力随着速度的增加又逐渐增大。之后，Johansson和Nielsen^[3]采用基于应变计原理的轮轨冲击载荷仪对带有车轮扁疤的货车进行了现场试验，测得了100 mm扁疤引起的最大垂向轮轨垂向冲击力与行车速度(30~100 km/h)之间的关系。理论研究方面，大量理论分析模型被用来预测车轮扁疤引起的轮轨冲击响应，其中绝大部分分析模型都基于赫兹接触理论，利用相对位移激励近似模拟车轮扁疤^[4-7]，但赫兹接触理论主要基于弹性半空间假设，很难准确描述轮轨冲击行为。最近，Pieringer等^[8]采用基于Kalker理论的三维非赫兹接触时域模型进行了不同尺寸新、旧车轮扁疤的仿真分析，对比分析了三维非赫兹接触模型、二维非赫兹接触模型和二维赫兹接触模型仿真结果^[9]的差异性。

与实验和理论研究相比，数值仿真在轮轨冲击分析中得到了更广泛的应用。大部分较早的数值仿真模型都基于多体系统动力学理论以及数值积分方法。Liu等^[10]利用多体动力学软件SIMPACK进行车轮扁疤引起的轮轨冲击和振动的分析。王忆佳等^[11]基于等效轨道激扰法和多体动力学理论对高速车辆的新、旧扁疤缺陷进行轮轨系统冲击响应的仿真分析，得出了车速和车轮扁疤长度对轮轨垂向冲击力的影响规律。翟婉明^[12]基于车辆-轨道耦合动力学理论采用快速积分方法编制了VICT模拟软件，并与实验结果进行对比，实现了轮轨系统冲击响应的快速数值模拟。但是上述仿真方法不能够很好地反映轮轨动态接触的非线性以及车轮扁疤几何的非线性。近年来，基于显式有限元法的三维轮轨滚动接触模型逐渐被应用到轮轨动态响应的仿真分析中^[13-14]。然而，现有三维滚动接触模型仿真分析均未考虑轮轨材料应变率效应对轮轨冲击响应的影响，尽管随着列车运行速度的不断提高，这种影响日渐显著。

因此，本研究利用Hypermesh软件建立带有扁疤的三维轮轨滚动接触模型，基于轮、轨钢Cowper-Symonds本构模型，采用显式非线性动力学分析软件LS-DYNA 3D模拟分析车轮扁疤引起的轮轨冲击响应，讨论车速、扁疤长度和轴重等关键参数对轮轨冲击响应的影响。

2.   轮、轨钢的Cowper-Symonds本构模型

研究对象为CRH3A型动车组轮轨系统：车轮为D1钢整体铸造车轮，其化学成分为Fe-0.5%C-0.306%Si-0.703%Mn-0.003%P-0.007%S-0.17%Cr-0.17%Ni-0.035%V；轨道为60 kg/m的U71Mn材质的钢轨。采用唯象本构模型Cowper-Symonds方程描述轮、轨钢的应变率敏感特性

式中:σ_d和σ_s分别为动态和准静态流动应力，$\[{\dot \varepsilon }\]$为应变率，C和P为拟合参数。

由于轮轨冲击载荷由车轮轮辋和钢轨直接承受，这里仅考虑轮辋钢和轨道钢的应变率相关本构特性。分别采用CMT5305型MTS万能试验机和分离式霍普金森杆(SHPB)装置开展轮辋钢的静、动态压缩力学性能试验，得到了不同应变率下轮辋钢的真实应力-真实应变响应曲线，如图 1所示。取真实应变0.06为参考应变值，得到不同应变率下的流动应力值，根据(1)式拟合得到轮辋钢的应变率相关参数C=45 635 s^-1和P=3.21。轨道钢的静、动态力学性质可由文献[15]获得，同样通过数据拟合得到轨道钢的Cowper-Symonds模型应变率相关参数C=1 733 s^-1和P=0.30。

图  1  不同应变率下轮辋钢的压缩真实应力-真实应变响应曲线

Figure  1.  Compressive true stress-strain response curves of rim steels at different strain rates

下载: 全尺寸图片 幻灯片

3.   轮轨滚动接触模型

采用Hypermesh有限元软件建立如图 2所示的三维滚动接触有限元模型。车轮半径为430 mm，踏面为S1002CN型；钢轨型面为CN60，轨底坡为1:40。为平衡计算效率和精度，车轮扁疤和钢轨接触区域的网格细化为4 mm×4 mm，其余区域网格尺寸为8 mm×8 mm。整个有限元模型包含516 629个节点，479 038个单元，并且均采用8节点实体单元划分。轮对(车轮与车轴)和钢轨的力学行为均采用*MAT_PLASTIC_KINEMATIC模型描述，仿真分析中输入的基本参数如表 1所示。钢轨底部节点所有自由度被约束，实现固支边界；而对车轴所有节点实施轴向平动约束，以保持轮对在滚动过程中的自平衡。对整个轮轨系统施加重力加速度，根据EN13104标准将轴重等效为两个集中力分别施加在车轴的两端，对于轴重17 t(即：轮对承受的机车或车辆质量为17 t)条件，两个集中力分别为110.41和77.56 kN。对车轮施加平动速度和相应的转动速度，同时对车轴施加和车轮相同的平动速度来实现轮对的初始速度条件。轮轨系统各部件之间定义自动面-面接触条件。

图  2  轮轨滚动接触模型(扁疤长度为40 mm)

Figure  2.  Finite element model of wheel-rail rolling contact with the flat length of 40 mm

下载: 全尺寸图片 幻灯片

表  1  车轮和钢轨的材料参数

Table  1.  Material parameters of wheel and rail

Part	Density/ (kg/m3)	Elasticity modulus/(GPa)	Poisson's ratio	Yield stress/ (GPa)	Tangent modulus/(GPa)	C/ (ms-1)	P
Rim	7 800	213	0.3	0.561	21	45.635	3.21
Web	7 800	216	0.3	0.395	21
Hub	7 800	213	0.3	0.417	21
Axle	7 800	206	0.3	0.560	20
Rail	7 800	193	0.3	0.525	19	1.733	0.3

下载: 导出CSV 

| 显示表格

4.   仿真结果与分析

4.1   典型的轮轨冲击响应特征

扁疤长度40 mm、轴重17 t和车速200 km/h条件下，典型的轮轨垂向冲击力时程曲线如图 3所示。可以看出，基于Cowper-Symonds模型得到的轮轨垂向冲击力曲线与不计轮轨材料应变率得到的轮轨垂向冲击力时程曲线完全重合，即轮轨材料的应变率效应对轮轨垂向冲击力没有影响。车轮扁疤引起的最大轮轨垂向冲击力(第1个峰值)出现在2.6 ms，其幅值为296 kN，大约为相应准静态垂向载荷(93.99 kN)的3.15倍。由于冲击响应时间较短(大约3 ms)，轮轨垂向冲击力来不及传递到轨下结构就已经消失，一般直接由钢轨承受，尤其是车轮扁疤处的接触区域，对车轮和钢轨表面疲劳损伤和塑性流动具有很大的影响。冲击过程中，由于钢轨弹性能的释放，钢轨对车轮向上的动态支撑力大于轮对系统的重力载荷，车轮会出现弹起现象，进而与钢轨脱离接触，此时的垂向冲击力为零。随后，车轮在重力作用下回落，对钢轨造成二次冲击(第2个峰值)，此时车轮旋转已越过扁疤区域；也就是说，第2个峰值力是由完整(不含扁疤)车轮和轨道冲击产生的轮轨垂向冲击力。显然，车轮扁疤引起的最大轮轨垂向冲击力明显大于不含扁疤的轮轨冲击力。

图  3  典型的轮轨垂向冲击力时程曲线

Figure  3.  Typical wheel-rail vertical impact force time-history curves

下载: 全尺寸图片 幻灯片

轮轨冲击过程中典型的von Mises等效应力和等效塑性应变的时程曲线分别如图 4(a)和图 4(b)所示。从图 4(a)可以看出：轮轨冲击发生之前，von Mises等效应力在很小的范围内波动；轮轨冲击发生后，von Mises等效应力随着响应时间增加发生大幅值的波动，在2.6 ms左右达到第1个峰值(由车轮扁疤引起)，并在3.0 ms左右达到最大值，分别为722 MPa(Cowper-Symonds模型)和689 MPa(不计及应变率)，都远超过了轮辋材料的屈服强度561 MPa，在长期运行过程中会导致轮辋的局部塑性变形。随后轮轨逐渐脱离接触，von Mises等效应力急剧减小并稳定在一个低应力水平，直至车轮非扁疤区域和钢轨发生二次冲击。轮轨冲击过程中，等效塑性应变也随着响应时间的增加而迅速增大，如图 4(b)所示。由于轮轨材料的应变率强化效应，基于Cowper-Symonds模型得到的最大von Mises等效应力明显更大，而其最大等效塑性应变(0.015)低于不计及应变率的仿真结果(0.017)。

图  4  典型的von Mises等效应力和等效塑性应变时程曲线

Figure  4.  Typical von Mises equivalent stress and equivalent plastic strain time-history curves

下载: 全尺寸图片 幻灯片

轮轨冲击过程中von Mises等效应力达到最大值时，沿车轮滚动方向轮轨截面上典型的von Mises等效应力云图如图 5所示。当等效塑性应变达到最大值时，沿车轮滚动方向轮轨截面上典型的等效塑性应变云图如图 6所示。从图 5和图 6可以看出，最大von Mises等效应力和最大等效塑性应变均发生在轮轨接触表面。较大的接触应力和塑性变形将会导致扁疤区域车轮材料的疲劳磨损和塑性流动，加剧扁疤缺陷的恶化；此外，较大的接触应力和塑性变形也可能导致轨顶压溃和轨腰大变形。综上所述，轮轨材料的应变率强化效应导致最大von Mises等效应力明显增大，而最大等效塑性应变略有降低。

图  5  典型的von Mises等效应力云图

Figure  5.  Typical von Mises equivalent stress contours

下载: 全尺寸图片 幻灯片

图  6  典型的等效塑性应变云图

Figure  6.  Typical equivalent plastic strain contours

下载: 全尺寸图片 幻灯片

4.2   车速对轮轨冲击响应的影响

图 7给出了3种不同扁疤长度工况下最大轮轨垂向冲击力和车速之间的关系。可以看出，材料的应变率效应对最大轮轨垂向冲击力没有影响，每种扁疤长度下最大轮轨垂向冲击力均随着车速的增大先增大，并在车速150 km/h时达到最大值，之后随着速度的增大而减小。可能的解释为^{[8, 16]}：轮轨冲击过程产生的巨大冲量迅速转化为车轮和钢轨的动量，轮轨逐渐脱离接触导致接触损失，当车速较低时，准静态轴重能够很好地维持轮轨接触，最大轮轨垂向冲击力随着速度的增加而增大；当车速较高时，轮轨接触力迅速增大到峰值，此时，轨道被迫向下运动，而车轮在惯性作用下仍暂时保持回落状态，导致轮轨垂向冲击力的削弱。

图  7  车速对最大轮轨垂向冲击力的影响

Figure  7.  Influence of train speed on maximum wheel-rail vertical impact force

下载: 全尺寸图片 幻灯片

不同扁疤长度工况下车轮最大von Mises等效应力随车速的变化如图 8所示。可以看出，不同扁疤长度下最大von Mises等效应力均随着车速的增加先增大后减小，且最大von Mises等效应力出现在车速为150~200 km/h时。图 9给出了不同扁疤长度下车轮最大等效塑性应变和车速的关系。可以看出，不同扁疤长度引起的最大等效塑性应变均随着速度的增加先增大，并在200 km/h时达到最大值，之后随着速度的增加而减小。此外，由Cowper-Symonds模型得到的最大von Mises等效应力显著大于不计应变率情况下得到的最大von Mises等效应力，而Cowper-Symonds模型得到的最大等效塑性应变小于不计应变率情况下得到的最大等效塑性应变。

图  8  不同扁疤长度引起的车轮最大von Mises等效应力与车速的关系

Figure  8.  Maximum von Mises equivalent stress of wheel induced by different flat lengths as a function of train speed

下载: 全尺寸图片 幻灯片

图  9  不同扁疤长度引起的车轮最大等效塑性应变和车速的关系

Figure  9.  Maximum equivalent plastic strain of wheel induced by different flat lengths as a function of train speed

下载: 全尺寸图片 幻灯片

4.3   扁疤长度对轮轨冲击响应的影响

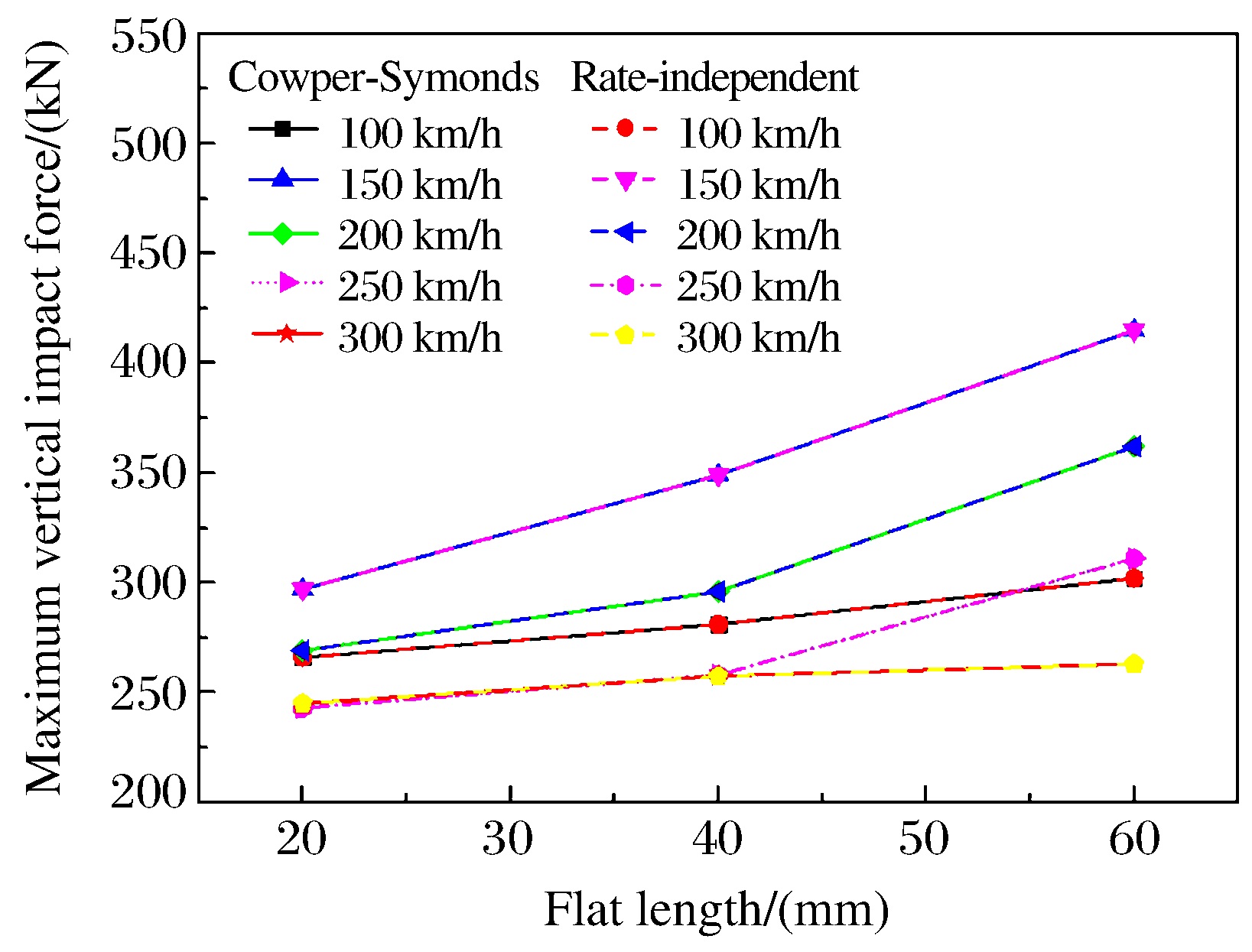
图 10给出了车速200 km/h、轴重17 t时最大轮轨垂向冲击力与扁疤长度之间的关系。可以看出，3种扁疤长度工况下轮轨材料的应变率效应对最大轮轨垂向冲击力没有影响；相同车速下，最大轮轨垂向冲击力随着扁疤长度的增大而增大。且低速(100 km/h)和高速(300 km/h)时，扁疤长度对最大轮轨垂向冲击力的影响很小；扁疤长度对最大轮轨垂向冲击力的影响在车速150~250 km/h范围内比较显著，尤其是当扁疤长度超过40 mm时。需要指出的是，150~250 km/h是高速列车的正常运行车速范围，因此，车轮扁疤对高速列车舒适性和安全性的影响应当引起足够的重视。

图  10  扁疤长度对最大轮轨垂向冲击力的影响

Figure  10.  Influence of flat length on maximum wheel-rail vertical impact force

下载: 全尺寸图片 幻灯片

图  11  车轮最大von Mises等效应力和扁疤长度的关系

Figure  11.  Maximum von Mises equivalent stress of wheel as a function of flat length

下载: 全尺寸图片 幻灯片

图  12  车轮最大等效塑性应变和扁疤长度的关系

Figure  12.  Maximum equivalent plastic strain of wheel as a function of flat length

下载: 全尺寸图片 幻灯片

4.4   扁疤长度对轮轨冲击响应的影响

图 13考察了5种轴重载荷(15、16、17、18和19 t)在扁疤长度为40 mm、车速200 km/h的工况下对轮轨垂向冲击力响应的影响。从图 13(a)可以看出：不同轴重工况下最大轮轨垂向冲击力对材料应变率是不敏感的；不同轴重下轮轨垂向冲击力-时间曲线类似，均随着轴重的增加而逐渐增大；车轮回落对钢轨造成二次冲击的时间间隔随着轴重的增加而稍有减小；无论是扁疤引起的最大轮轨垂向冲击力(第1个峰值)还是完整车轮与钢轨之间的最大轮轨垂向力(第2个峰值)均随着轴重的增加而增大。不同扁疤长度下，最大轮轨垂向冲击力均随着轴重的增加而近似呈线性增大，且最大轮轨垂向冲击力随轴重增加的增长率近似相等，如图 13(b)所示。

图  13  轴重对轮轨垂向冲击力响应的影响

Figure  13.  Influence of axle load on the wheel-rail vertical impact force response

下载: 全尺寸图片 幻灯片

图 14(a)和图 14(b)分别给出了不同扁疤长度引起的车轮最大von Mises等效应力、最大等效塑性应变和轴重的对应关系。可以看出，不同扁疤长度下最大von Mises等效应力和最大等效塑性应变均随着轴重的增加而近似呈线性增大。与上述仿真结果相同，不同轴重工况下轮轨材料的应变率效应能够显著增大车轮的最大von Mises等效应力，减小其最大等效塑性应变。

图  14  车轮最大von Mises等效应力、最大等效塑性应变和轴重的关系

Figure  14.  Maximum von Mises equivalent stress and maximum equivalent plastic strain of wheel as a function of axle load

下载: 全尺寸图片 幻灯片

5.   结论

利用Hypermesh有限元软件建立了带有扁疤的三维滚动接触模型，采用显式非线性动力学分析软件LS-DYNA模拟了基于Cowper-Symonds模型的铁路车轮扁疤引起的轮轨冲击响应，着重分析了车速、扁疤长度和轴重对轮轨垂向冲击力、von Mises等效应力和等效塑性应变的影响，得到了如下主要结论。

(1) 车轮扁疤引起的最大轮轨垂向冲击力显著大于相应的准静态垂向载荷，最大von Mises等效应力和最大等效塑性应变发生在轮轨接触表面。轮轨材料应变率效应对轮轨垂向冲击力没有影响，但对最大von Mises等效应力和最大等效塑性应变影响较大。

(2) 不同扁疤长度下，最大轮轨垂向冲击力和最大von Mises等效应力均随着车速的增加先增大，在车速为150~200 km/h时达到最大值，之后随着速度的增加而减小；而最大等效塑性应变和车速之间呈非单调变化关系。

(3) 不同车速引起的最大轮轨垂向冲击力和最大von Mises等效应力均随着扁疤长度的增大而增大，且在150~250 km/h车速范围内扁疤长度对最大轮轨垂向冲击力的影响最为显著；而最大等效塑性应变和扁疤长度之间呈非单调变化关系。

(4) 相同扁疤长度下，最大轮轨垂向冲击力、最大von Mises等效应力和最大等效塑性应变均随着轴重的增加而近似呈线性增大。