1.   引言

核幔边界D^〃层以其不均匀、不连续、强各向异性以及存在超低声速区等特殊的性质吸引了人们的研究注意, 希望通过揭示这一区域的物理化学组分和性质来深入了解地震波的传播规律以及地球的演化过程。2004年, Oganov等提出的后钙钛矿相MgSiO₃(Post-Perovskite pPv)被认为是在D^〃层条件下的主要物质^[1-2], 因为从钙钛矿相(Pv)到pPv的转变会引起MgSiO₃密度的增加以及各向异性的增强^[3-4], 这与已经观测到的结果吻合。Fe是地核以及下地幔的重要元素之一, 其性质必定会对D^〃层的性质产生影响。已有研究结果表明, 外界条件(温度、压强等)会对Fe的微观状态(主要是自旋)产生影响, 而反过来Fe的微观状态又会对矿物的弹性性质、地震波速以及热力学性质产生影响^[5-9]。对于后钙钛矿相MgSiO₃中Fe的自旋状态现在还没有一致的结论, Caracas等的计算结果表明在D^〃条件下Fe²⁺为高自旋状态^[10], 而Lin等的实验结果则显示Fe²⁺在高压下为中间自旋态^[11]。因此Fe的微观状态以及这些结果的差异还需要进一步的研究。近年来, 第一性原理计算成功应用于方镁石和钙钛矿等矿物的研究中, 为高温高压下矿物的性质研究提供了一种行之有效的方法^[12-13]。前人利用第一性原理对含铁pPv也做了一些研究, 但都是固定在某一特定浓度下进行讨论的^{[3, 14]}。地球核幔间元素的交换以及D^〃层中元素的不均匀必定会导致Fe元素浓度的不一致, 已有研究结果也证实了与Pv相比, pPv中可能存在较高含量的Fe^[8-15-16]。因此采用第一性原理计算对含不同Fe²⁺浓度的pPv的自旋状态及地震波特征进行了研究。对于含有多个Fe²⁺的结构, 计算了各种可能位置的能量, 结合力学稳定性判据, 给出了Fe²⁺在pPv中的占据位置。最后, 在120 GPa(D^〃层压强)下对不同Fe²⁺浓度的弹性波速以及各向异性进行了计算, 阐明了Fe²⁺的浓度对其的影响。

2.   计算模型与方法

图 1为pPv的结构图, 属于正交晶系CMCM空间群, 具有明显的分层特性, Si和O组成边角相连的正八面体, Si原子位于正八面体的中心, O原子位于正八面体的顶点, Mg原子位于层间的正八面体之间, 见图 1中绿色小球。在本研究的计算中选取2×1×1含有40个原子的超晶胞, 并用不同个数的Fe²⁺分别替代Mg²⁺, 来达到改变Fe²⁺浓度的目的。本研究所有的计算均采用以密度泛函以及平面波赝势为基础的CASTEP软件, 计算中考虑了Fe²⁺电子的自旋极化, 交换关联能选用广义梯度近似(GGA)中的PBE泛函形式^[17-18]。分别在选取截断能为340 eV和310 eV的情况下进行了计算, 结果表明两种截断能的选择对结果的影响不大, 因此为提高计算的效率, 本研究选取截断能为310 eV, K网格点设为4×2×3。在几何优化时, 保证离子间的作用力小于0.5 eV/nm, 能量以及位移收敛度分别设为20 μeV和0.2 pm。弹性常数的计算采用应力-应变关系^[19], 并且离子间作用力以及能量、位移收敛度分别设为0.1 eV/nm、4 μeV和0.04 pm。

图  1  后钙钛矿相MgSiO₃(pPv)结构图

Figure  1.  Structure of post-perovskite MgSiO₃

下载: 全尺寸图片 幻灯片

3.   结果与讨论

3.1   Fe²⁺的浓度对不同自旋态的影响

根据Fe²⁺离子d电子自旋的不同组合, 本研究考虑了3种不同的自旋状态:高自旋态HS(S=2)、中间自旋态IS(S=1)以及低自旋态LS(S=0)^[20], 如表 1所示。

表  1  Fe²⁺的不同自旋排列以及对应自旋态

Table  1.  Various spin arrangement and corresponding spin states of Fe²⁺

Spin states	Fe2+(3d6)
HS(S=2)	↑↓	↑	↑	↑	↑
IS(S=1)	↑↓	↑↓	↑	↑
LS(S=0)	↑↓	↑↓	↑↓
Note:↑ represents spin up, ↓ represents spin down.

下载: 导出CSV 

| 显示表格

图 2给出了不同压强以及不同浓度(物质的量分数)的各个自旋态的焓差值, 通过比较焓值的大小可以确定体系稳定的自旋状态。从图中可以看到, 从0到160 GPa的压强范围内, 不同浓度所对应的高自旋状态始终具有最小的焓值, 但是随着压强的增加, 有转向中间自旋态和低自旋态的趋势。Fe²⁺的浓度对曲线斜率的影响主要表现在低自旋态与高自旋态的焓差曲线(图 2(b)所示), 而对于中间自旋态与高自旋态的焓差曲线(图 2(a)所示)的斜率基本没有影响, 在低浓度范围, 虚线的变化明显快于实线, 因此在高压下容易发生从高自旋到低自旋的转变, 相反在高浓度范围内, 实线的变化快于虚线, 因此在高压下会发生从高自旋到中间自旋的转变。图中显示出另一个明显的特征是低浓度和高浓度所对应的焓差曲线位于中间浓度对应的焓差曲线的下方, 并且中间浓度对应的焓差曲线随压强变化剧烈, 表明压强对中间浓度含铁pPv的影响大于低浓度和高浓度时的情形。实验中观测到的Fe²⁺不同自旋态以及不同的自旋转变可能正是由于在实验中Fe²⁺的浓度的不同所致。

图  2  Fe²⁺不同自旋态的焓差随压强的变化关系

Figure  2.  Pressure dependence of relative enthalpies(ΔH) of Fe²⁺ with different spin states

下载: 全尺寸图片 幻灯片

图 3为选取强关联U=4 eV^[5]时0 GPa以及120 GPa时Fe²⁺的d电子的态密度图, 从图 3可以看出, 与0 GPa时相比, 120 GPa时近费米面的自旋向下的态密度明显减小, 主要是转移到深能级的自旋向上的地方, 因此自旋极化减小, 而Fe²⁺的磁矩也从3.82 μB减小为3.64 μB, 这可能正是从高自旋状态转向中间自旋或低自旋状态转变的趋势。

图  3  0和120 GPa时Fe²⁺的d电子的态密度图

Figure  3.  Density of states of d electrons of Fe²⁺ at 0 and 120 GPa

下载: 全尺寸图片 幻灯片

3.2   pPv中Fe²⁺的占据位置

当Fe²⁺的浓度为37.5%、50.0%、67.5%以及75.0%时(图 1结构中分别有3、4、5和6个Mg²⁺被Fe²⁺取代), 计算考虑了Fe²⁺处于不同的位置时的能量, 图 4给出了浓度为37.5%和50.0%时各种可能结构以及其对应的焓值(图 4中为MgSiO₃去掉Si—O正八面体的结构)。

图  4  Fe²⁺不同浓度时的不同结构(只给出了Fe和Mg元素(绿色为Mg原子、紫色为Fe原子)，(a)、(h)、(m)、(n)分别为浓度为37.5%、50.0%、67.5%、75.0%时的最稳定结构)

Figure  4.  Different structures of various concentration of Fe²⁺(only the Fe and Mg atoms presented, and the green and purple balls denote Mg and Fe, respectively), where (a), (h), (m), (n) are the most stable structure for the concentration of 37.5%, 50.0%, 67.5%, 75.0%, respectively

下载: 全尺寸图片 幻灯片

首先通过计算确定出两个Fe²⁺以最近邻方式占据图 4(a)中的1和2位置时最稳定, 然后依次改变其他Fe²⁺的位置。Fe²⁺的浓度为37.5%的pPv有如图 4(a)~图 4(e)所示的5种可能结构。比较5种可能结构的焓值, 可以确定结构(a)为最稳定结构, 即3个Fe²⁺组成xOz平面上的等腰三角形, 这也是3个Fe²⁺原子排列最为紧密的情况, 与已知的过渡金属掺杂结构吻合。对于含Fe²⁺浓度为50.0%的时候, 考虑了如图 4(f)~图 4(l)所示的7种可能结构, 从各结构的焓值可以看出, 当Fe²⁺原子排列为xOz平面上的平行四边形时能量最低, 上下两层分别含有3个和1个Fe²⁺时, 能量次之, 而上下两层分别占据两个Fe²⁺原子时能量最高。但是计算得到的弹性常数显示结构(f)中的C₄₄ < 0, 这与已知的正交晶系力学稳定性判据要求不符, 说明结构(f)不满足力学稳定性。这种力学的不稳定性可能由于层与层完全不同的原子之间作用力的不同, 从而导致在应力作用下形变的不协调。而能量紧次之的结构(h)的弹性常数符合正交晶系力学稳定性要求, 因此在后续计算中, 选取结构(h)作为含Fe²⁺量为50.0%的稳定结构。含Fe²⁺的浓度为67.5%和75.0%时的稳定结构如图 4(m)和图 4(n)所示。综合不同浓度时的稳定结构推测, 作为杂质掺入pPv中的Fe²⁺倾向于以最紧密的方式替换pPv中的Mg²⁺。

3.3   pPv中Fe²⁺的浓度对弹性常数的影响

从上面的结果可以看出, 高自旋为最稳定的状态, 因此在以下的弹性性质计算中都基于高自旋状态的结构。由正交晶系的性质可得pPv弹性常数矩阵具有如下的形式

表 2列出了120 GPa时Fe²⁺的浓度为12.5%和1时以及本征MgSiO₃的各个弹性常数。从表中可以看到, 与本征pPv类似^[21], 无论Fe²⁺的浓度大小, 与C₁₁、C₃₃相比, C₂₂始终是最小的, 这是由于pPv的层状结构所致, 使得其沿b轴最容易压缩。与本征MgSiO₃相比, 含Fe²⁺导致C₁₁和C₃₃增加, 而C₂₂减小, 但随着浓度的增加C₁₁、C₂₂和C₃₃均有减小, 表明随着Fe²⁺的浓度的增加, 结构更易发生正形变。对于剪切形变, 从表 2中可以看出, 高浓度的Fe²⁺使剪切弹性常数有很大的减小, 其中C₄₄尤为明显, 而这种形变可能引起层与层之间正八面体通过角上的O原子相互连接, 从而发生从后钙钛矿相到钙钛矿相的逆转变。

表  2  120 GPa时含不同Fe²⁺浓度的pPv的弹性常数

Table  2.  Elastic constants of pPv at 120 GPa with different concentrations of Fe²⁺ (GPa)

Concentration	C11	C22	C33	C12	C13	C23	C44	C55	C66
0	1 200	941	1 158	375	274	450	277	248	377
0.125	1 215	881	1 172	403	318	460	260	248	388
1	1 089	815	1 049	414	377	457	64	202	259

下载: 导出CSV 

| 显示表格

图 5为体变模量B以及剪切模量G随Fe²⁺浓度的变化图, 可以看出, Fe²⁺浓度的增加使剪切模量G减小, 而对于体变模量B影响较小。

图  5  体积模量B以及剪切模量G随Fe²⁺物质的量分数的变化

Figure  5.  Bulk modulus (B) and shear modulus (G)as a function of mole fraction of Fe²⁺

下载: 全尺寸图片 幻灯片

3.4   Fe²⁺的浓度对弹性波速的影响

压缩波波速v_P和剪切波波速v_S分别定义为

式中:B、G分别为体积模量以及剪切模量, ρ为密度。

压缩波波速和剪切波波速随浓度的变化关系如图 6所示。可以看出, Fe²⁺使v_P和v_S都有明显的减小, 与本征MgSiO₃相比, 当Fe²⁺的浓度为50.0%的时候, v_P和v_s分别减小7.98%和12.73%, 当Fe²⁺的浓度为1时, v_P和v_S分别减小19.29%和31.73%, 因此Fe²⁺的浓度的不同可能是引起D^〃层波速异常以及形成超低声速区的原因之一^[22]。

图  6  压缩波和剪切波波速随Fe²⁺物质的量分数的变化

Figure  6.  Compression waves and shear wavesas a function of mole fraction of Fe²⁺

下载: 全尺寸图片 幻灯片

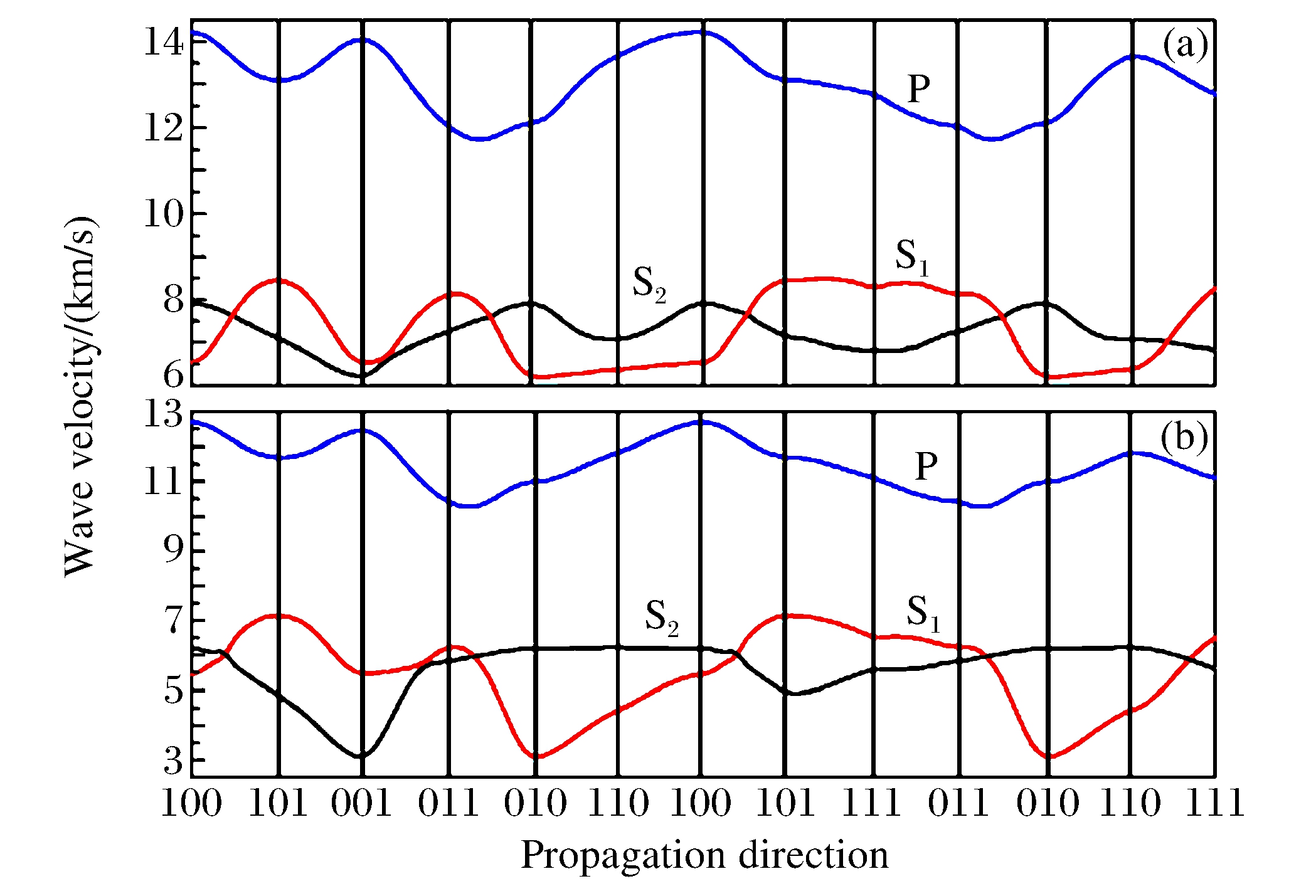
通过求解Cristoffel方程|c_ijlkn_jn_l-ρV²δ_ik|=0可以得到不同传播方向上的弹性波速^[23], 图 7给出了Fe²⁺的浓度分别为12.5%和1时的波速图。从图 7可以看出, 对于P波, 曲线的形状基本一样, 最快传播方向为[100], 而最慢传播方向位于[011]和[010]之间。对于S波, Fe²⁺的浓度虽然没有改变最快与最慢传播方向, 分别为[101]和[001], 但对于曲线在[010]到[100]之间的变化影响较大, 这主要源于不同浓度C₄₄与C₆₆之间的较大差异(见表 2)。

图  7  Fe²⁺的物质的量分数分别为12.5%(a)和1(b)时P波和S波沿不同传播方向的波速

Figure  7.  P-wave and S-wave velocities in different propagation directions for the Fe²⁺ mole fraction of 12.5%(a)and 1(b) respectively

下载: 全尺寸图片 幻灯片

S波的横向各向异性定义为: 其中v_SH、v_SV分别表示S波的水平极化和垂直极化分量, v_S为S波平均波速。图 7给出了S波分别以[100]、[010]和[001]为对称轴的横向各向异性。从图 7可以看出, 横向各向异性在不同的对称轴下可以取相反的符号, 即v_SH > v_SV与v_SH < v_SV均有可能存在, 而随着Fe²⁺的浓度的增加, 横向各向异性都有增强, 尤其在高浓度区更为明显。

4.   总结

运用第一性原理的计算方法, 计算讨论了pPv含有不同浓度的Fe²⁺时对其结构以及性质的影响。计算结果表明, Fe²⁺在0~160 GPa的压力范围内始终保持为高自旋状态, 而与Fe²⁺的浓度无关, 但在高压下有转向中间自旋态或低自旋态的趋势。对于含有多个Fe²⁺的情况, 通过比较不同位置的能量以及结合力学稳定判据, 给出了Fe²⁺的占据位置, 结果表明Fe²⁺倾向于以最紧密的方式替换pPv中的Mg²⁺。计算得到的弹性波速结果显示无论P波还是S波, Fe²⁺都会降低其波速, 而D^〃层超低声速区的形成可能正是由于Fe含量的增加。已有地震观测数据显示, D^〃层存在明显的横向各向异性, S波的水平极化分量明显大于其垂直极化分量, 即v_SH > v_SV, 而本研究结果显示, 在以b轴和c轴为对称轴的时候可以产生这样的结果, 与观测结果一致。随着Fe²⁺的浓度的增加, 在高浓度区可以产生很强的横向各向异性, 因此, 富Fe区可能是形成D^〃层强各向异性区域的原因之一。